acwing 532.货币系统

https://www.acwing.com/problem/content/534/

 

 

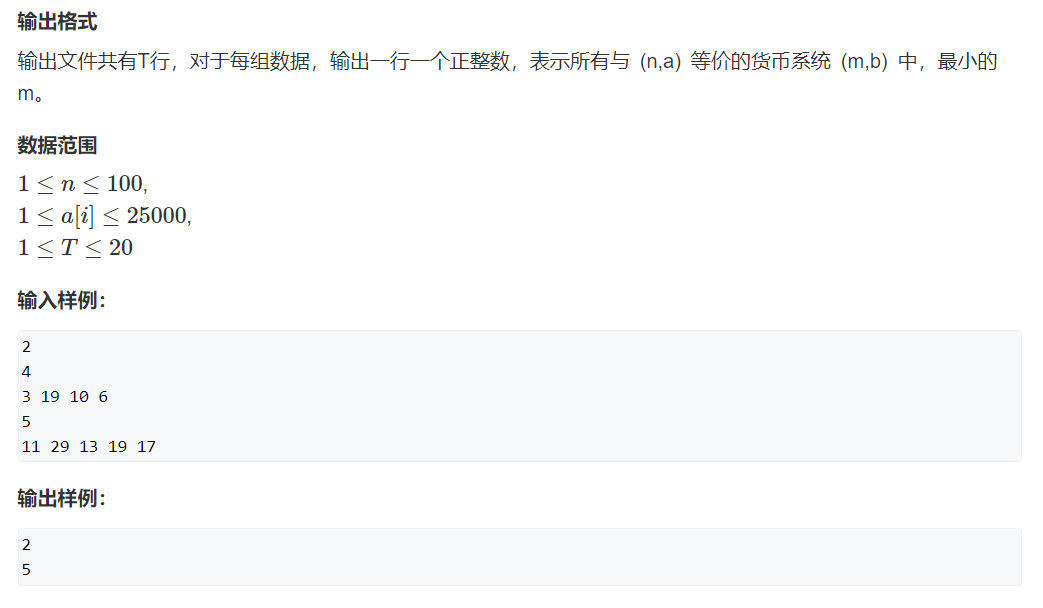
 题意：求一个更短的序列$b$，使得他能表示序列$a$所能表示的所有的数，并且不能表示$a$不能表示的所有的数。

分析该题，有以下性质：

①$a_1, a_2, a_3, \cdot \cdot \cdot, a_i$一定都可以被$b_i$所表示出来。

因为$b_i$必须能表示$a_i$的所有数，才能表示出$a_i$所能表示的所有的数。

②最优解的$b_1, b_2, b_3, \cdot \cdot \cdot, b_i$一定不能被其他的$b_i$所表示。

因为能被其他的$b_i$所表示，说明当前这个数是多余的，可以去掉，减短序列长度。

③最优解序列$b$的元素一定是从序列$a$的元素中选出的。

假设最优解的序列$b$的元素不是序列$a$中的元素，因为两个集合中所表示的数是一样的，所有$b$序列中的一个数字$b_i$可以由$a$中的元素所表示。

而$a$中的元素也可以由$b$中的元素表示，所以$b_i$可以由$b$中的元素所表示。

与性质②矛盾，所以最优解的序列$b$中的元素一定是从序列$a$中选出的。

思路：将数字从小到大排列，跑一遍完全背包，体积最大的边界就是数组中最大的元素。

如果当前数的方案为$0$说明当前数无法由前面的数表示，答案数加$1$。

代码：

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 110, M = 25010;
int f[M];
int a[N];
int n, m;

int main(){
    int T;
    cin >> T;
    while(T --)
    {
        cin >> n;
        for(int i = 1 ; i <= n ; i ++)cin >> a[i];
        sort(a + 1, a + n + 1);
        
        
        m = a[n];
        memset(f, 0, sizeof f);
        f[0] = 1;
        int res = 0;
        for(int i = 1 ; i <= n ; i ++)
        {
            if(!f[a[i]])res ++;
            for(int j = a[i] ; j <= m ; j ++)
                f[j] += f[j - a[i]];
        }    
        cout << res << endl;
    }
    
    return 0;
}