背包dp

三种初始化方式：

①当体积最多是$j$的时候：数组$f$全部初始化为$0$，且保证体积一定大于等于$0$$(memset(f, 0, sizeof f）, v >= 0)$。

②当体积恰好是$j$的时候：除了第一个元素，数组$f$全部初始化为无穷大，且保证体积一定大于等于$0$$(memset(f, 0x3f, sizeof f), f[0] = 0, v >= 0)$。

③当体积至少是$j$的时候：同②，区别就是不用保证体积一定大于等于$0$$(memset(f, 0x3f, sizeof f), f[0] = 0)$。

01背包问题

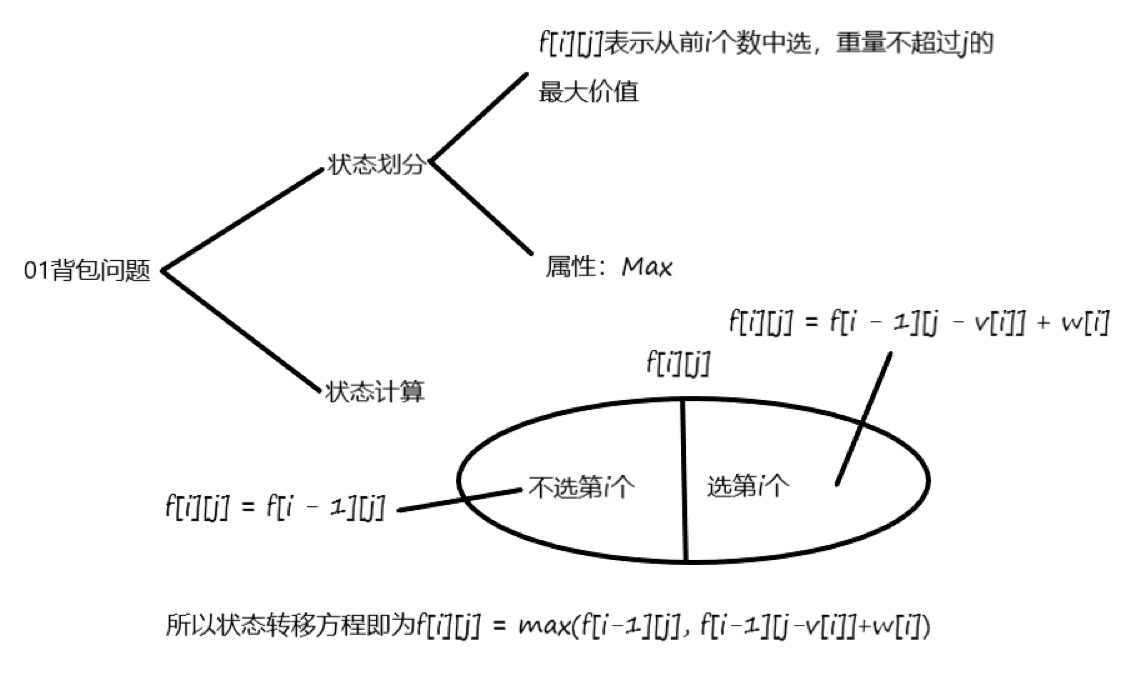
而我们所求的结果就是$f[n][m]$。

 1 #include <iostream>
 2 #include <algorithm>
 3 
 4 using namespace std;
 5 
 6 
 7 const int N = 1010;
 8 int v[N], w[N];
 9 int f[N][N];
10 int n, m;
11 
12 int main(){
13     cin >> n >> m;
14     for(int i = 1 ; i <= n ; i ++)cin >> v[i] >> w[i];
15     
16     for(int i = 1 ; i <= n ; i ++)
17         for(int j = 0 ; j <= m ; j ++)
18         {
19             f[i][j] = f[i - 1][j];
20             if(j >= v[i])f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
21         }
22     cout << f[n][m] << endl;
23     return 0;
24 }

优化：

由于计算$f[i][j]$，即第$i$层的时候，只用到了$i-1$层的状态，所以是可以考虑优化掉一维的数组的。当拿掉一维后，$f[i][j] = f[i-1][j] \leftrightarrow f[j] = f[j]$，式子等价，直接删除。而对于$f[i][j] = max(f[i][j], f[i-1][j-v[i]]+w[i])$来说，因为目前要计算的状态是由上一层的当前状态$A$和上一层的当前状态的前一个状态$B$转移过来。所以在计算当前状态的时候，$B$已经被更新成了当前层的状态，即$f[i-1][j-v[i]]$已经变成了$f[i][j-v[i]]$，所以是不能按顺序进行更新的，而当$j$从大到小逆序枚举时，该式子就可以直接去掉一维，依旧是等价的。

 1 int main(){
 2     cin >> n >> m;
 3     for(int i = 1 ; i <= n ; i ++)cin >> v[i] >> w[i];
 4     
 5     for(int i = 1 ; i <= n ; i ++)
 6         for(int j = m ; j >= v[i] ; j --)
 7             f[j] = max(f[j], f[j - v[i]] + w[i]);
 8     cout << f[m] << endl;
 9     return 0;
10 }

完全背包问题

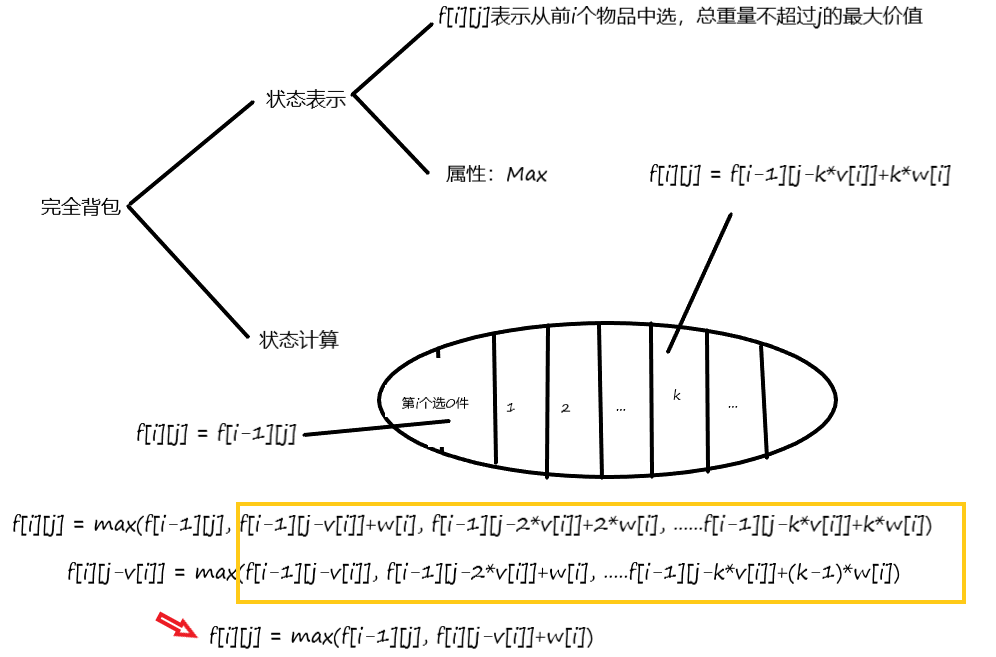
如同$01$背包，但是注意的是当前需要计算的状态是由上一层的当前状态$A$和当前层的当前状态的前一个状态$B$转移过来，而当$j$按顺序枚举时，在计算当前状态的时候，$B$已经被算出，可以直接转移，所以在去掉一维数组后，$j$是按顺序枚举的。

 1 #include <iostream>
 2 #include <algorithm>
 3 
 4 using namespace std;
 5 
 6 const int N = 1010;
 7 int f[N], w[N], v[N];
 8 int n, m;
 9 
10 int main(){
11     cin >> n >> m;
12     for(int i = 1 ; i <= n ; i ++)cin >> v[i] >> w[i];
13     
14     for(int i = 1 ; i <= n ; i ++)
15         for(int j = v[i] ; j <= m ; j ++)
16             f[j] = max(f[j], f[j - v[i]] + w[i]);
17     
18     cout << f[m] << endl;
19     return 0;
20 }

多重背包问题

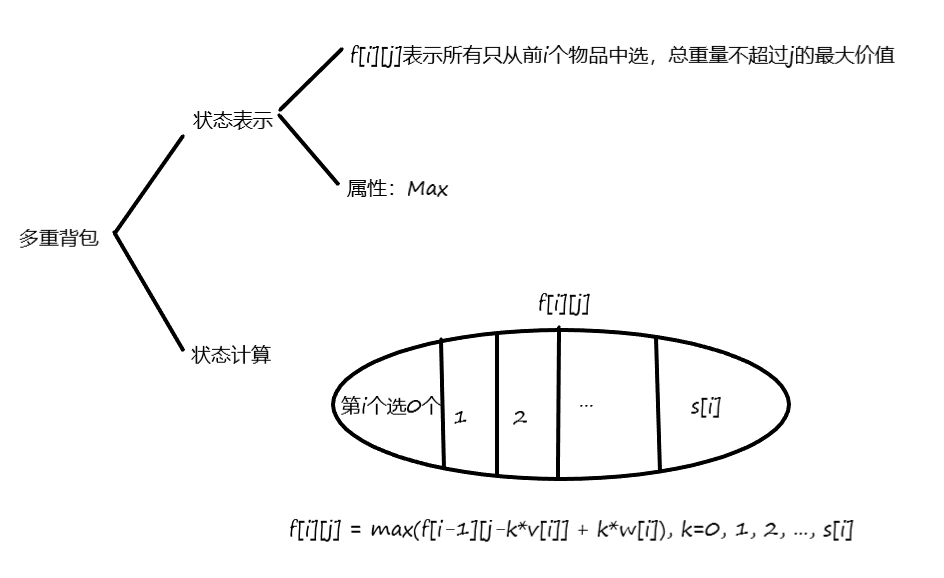
朴素版本：时间复杂度$O(NMS)$

 1 #include <iostream>
 2 #include <algorithm>
 3 
 4 using namespace std;
 5 
 6 const int N = 110;
 7 
 8 int n, m;
 9 int v[N], w[N], s[N];
10 int f[N][N];
11 
12 int main()
13 {
14     cin >> n >> m;
15 
16     for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i] >> s[i];
17 
18     for (int i = 1; i <= n; i ++ )
19         for (int j = 0; j <= m; j ++ )
20             for (int k = 0; k <= s[i] && k * v[i] <= j; k ++ )
21                 f[i][j] = max(f[i][j], f[i - 1][j - v[i] * k] + w[i] * k);
22 
23     cout << f[n][m] << endl;
24     return 0;
25 }

优化：

二进制优化：

枚举一个数字的时候，例如枚举$37$这个数字，可以将其分为$1，2，4，8，16，32， 5$。我们可以用这$7$个数字，拼凑出$0$到$36$中的任何一个数。所以用这种方法枚举会比一个个枚举更加高效。

这样，就能将$s$的循环从$O(n)$优化为$O(logn)$的复杂度。

时间复杂度$O(NMlogS)$

 1 #include <iostream>
 2 #include <algorithm>
 3 
 4 using namespace std;
 5 
 6 const int N = 12010, M = 2010;
 7 
 8 int n, m;
 9 int v[N], w[N];
10 int f[M];
11 
12 int main()
13 {
14     cin >> n >> m;
15 
16     int cnt = 0;
17     for (int i = 1; i <= n; i ++ )
18     {
19         int a, b, s;
20         cin >> a >> b >> s;
21         int k = 1;
22         while (k <= s)
23         {
24             v[++ cnt] = a * k;
25             w[cnt] = b * k;
26             s -= k;
27             k *= 2;
28         }
29         if (s > 0)
30         {
31             v[++ cnt] = a * s;
32             w[cnt] = b * s;
33         }
34     }
35 
36     //跑一遍01背包
37     for (int i = 1; i <= cnt; i ++ )
38         for (int j = m; j >= v[i]; j -- )
39             f[j] = max(f[j], f[j - v[i]] + w[i]);
40 
41     cout << f[m] << endl;
42 
43     return 0;
44 }

分组背包问题

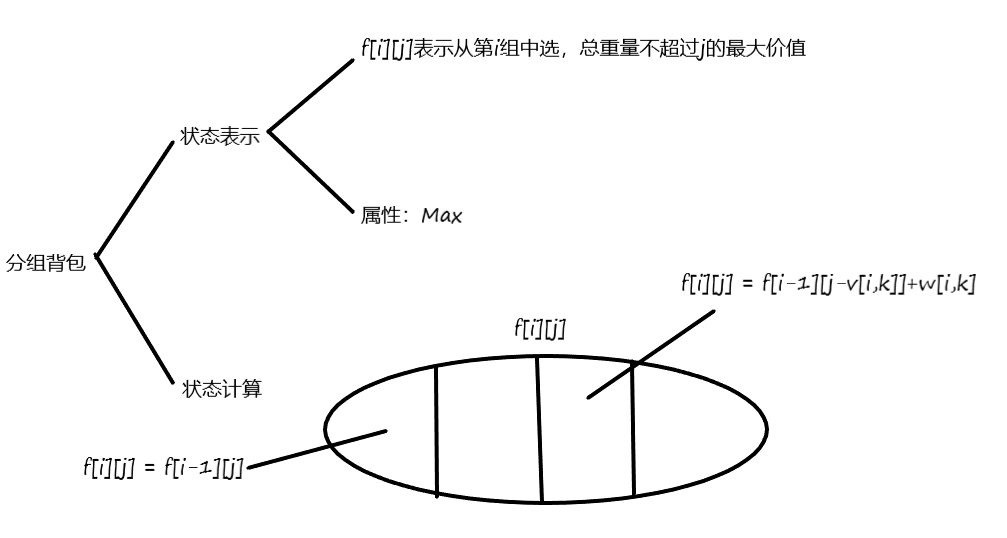
$for$ 物品

　　$for$ 体积

　　　　$for$ 决策

 1 #include <iostream>
 2 #include <algorithm>
 3 
 4 using namespace std;
 5 
 6 const int N = 110;
 7 
 8 int n, m;
 9 int v[N][N], w[N][N], s[N];
10 int f[N];
11 
12 int main()
13 {
14     cin >> n >> m;
15 
16     for (int i = 1; i <= n; i ++ )
17     {
18         cin >> s[i];
19         for (int j = 0; j < s[i]; j ++ )
20             cin >> v[i][j] >> w[i][j];
21     }
22 
23     for (int i = 1; i <= n; i ++ )
24         for (int j = m; j >= 0; j -- )
25             for (int k = 0; k < s[i]; k ++ )
26                 if (v[i][k] <= j)
27                     f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
28 
29     cout << f[m] << endl;
30 
31     return 0;
32 }

混合背包问题

混合背包问题其实就将$01$背包，完全背包，多重背包问题混合起来，关键在于物品的个数$s$。如果$s$为$1$，那么当前就用$01$背包更新;如果$s$有无限个，那么当前就用完全背包更新;如果$s$有限个且大于$1$，那么当前就用多重背包更新。其中$01$背包属于多重背包的特殊情况，可以合并起来。

acwing 7.混合背包问题

https://www.acwing.com/problem/content/7/

 1 #include <iostream>
 2 #include <algorithm>
 3 
 4 using namespace std;
 5 
 6 const int N = 1010;
 7 
 8 int n, m;
 9 int f[N];
10 
11 int main()
12 {
13     cin >> n >> m;
14 
15     for (int i = 0; i < n; i ++ )
16     {
17         int v, w, s;
18         cin >> v >> w >> s;
19         if (!s)
20         {
21             for (int j = v; j <= m; j ++ )
22                 f[j] = max(f[j], f[j - v] + w);
23         }
24         else
25         {
26             if (s == -1) s = 1;
27             for (int k = 1; k <= s; k *= 2)
28             {
29                 for (int j = m; j >= k * v; j -- )
30                     f[j] = max(f[j], f[j - k * v] + k * w);
31                 s -= k;
32             }
33             if (s)
34             {
35                 for (int j = m; j >= s * v; j -- )
36                     f[j] = max(f[j], f[j - s * v] + s * w);
37             }
38         }
39     }
40 
41     cout << f[m] << endl;
42 
43     return 0;
44 }

二维费用背包问题

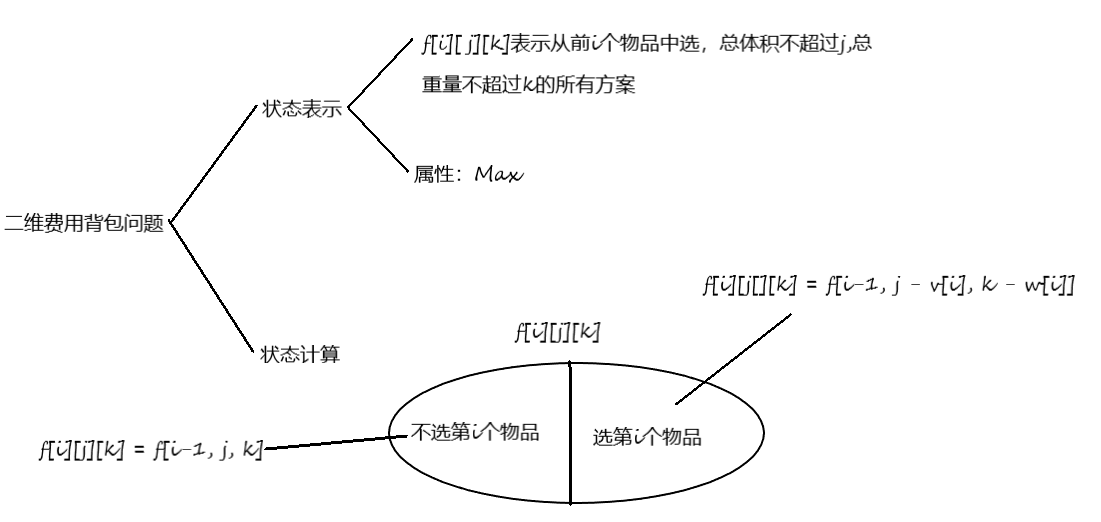
https://www.acwing.com/problem/content/1022/

acwing 1020.潜水员

本题的条件是至少需要有$j$的体积，至少要有$k$的质量，分析方式和上方的图相同。唯一不同的是当数组的$j$和$k$的两个维度是可以为负数的，这时候将他们置成$0$就可以。

 1 #include <iostream>
 2 #include <algorithm>
 3 #include <cstring>
 4 
 5 using namespace std;
 6 
 7 const int N = 1010;
 8 int f[N][N];
 9 
10 int main(){
11     int n, V1, V2;
12     cin >> V1 >> V2 >> n;
13     memset(f, 0x3f, sizeof f);
14     f[0][0] = 0;
15     for(int i = 1; i <= n ; i ++)
16     {
17         int v1, v2, w;
18         cin >> v1 >> v2 >> w;
19         for(int j = V1; j >= 0 ; j --)
20             for(int k = V2; k >= 0 ; k --)
21                 f[j][k] = min(f[j][k], f[max(0, j - v1)][max(0, k - v2)] + w);
22     }
23     cout<<f[V1][V2]<<endl;
24     return 0;
25 }

https://www.acwing.com/problem/content/1024/

acwing 1022.宠物小精灵之收服

典型的二维费用背包，$f[i][j][k]$表示的是从前$i$只小精灵中选，精灵球总数不超过$j$个，皮卡丘消耗的体力不超过$k$的所有方案。需要注意的是，题中表示$k$不能为为$0$，即说明循环时需要从$V_2-1$开始枚举，而不是从$V_2$开始枚举。

 1 #include <iostream>
 2 #include <algorithm>
 3 
 4 using namespace std;
 5 
 6 const int N = 1010;
 7 int f[N][N];
 8 int n, V1, V2;
 9 
10 int main(){
11     cin >> V1 >> V2 >> n;
12     
13     for(int i = 1 ; i <= n ; i ++)
14     {
15         int v1, v2;
16         cin >> v1 >> v2;
17         for(int j = V1 ; j >= v1 ; j --)
18             for(int k = V2 - 1 ; k >= v2 ; k --)
19                 f[j][k] = max(f[j][k], f[j - v1][k - v2] + 1);
20     }
21     int m = V2 - 1;
22     while(m > 0 && f[V1][V2 - 1] == f[V1][m - 1])m --;
23 
24         
25     cout << f[V1][V2 - 1] << " " << V2 - m << endl;
26     return 0;
27 }

背包问题求具体方案,方案数

对于$01$背包来说，容易得到背包问题的方案数的转移方程是$f[i][j] = f[i-1][j] + f[i-1][j-v]$, 简化成一维$f[j] += f[j-v]$。

①若要求具体的方案，就和做最短路一样的。从后开始往前推，如果当前的状态$A$是由前面一个状态$B$转移过来的，就走到$B$上。这样可以推到开头可以得到具体的方案。

若要求的是最小字典序，可以反着做一遍背包，再倒推。这样得到的就是最小字典序。类似与最短路的路径输出。

acwing 12.求背包的具体方案数

https://www.acwing.com/problem/content/12/

②方案数：依旧是类似最短路一样从后往前推导。

acwing 11.背包问题求方案数

https://www.acwing.com/problem/content/11/

 1 #include <iostream>
 2 #include <algorithm>
 3 
 4 using namespace std;
 5 
 6 const int N = 1010, mod = 1e9 + 7;
 7 int f[N], g[N];
 8 int n, m;
 9 
10 int main(){
11     cin >> n >> m;
12     f[0] = 0, g[0] = 1;
13     
14     for(int i = 1 ; i <= n ; i ++)
15     {
16         int v, w;
17         cin >> v >> w;
18         for(int j = m ; j >= v ; j --)
19         {
20             int maxv = max(f[j], f[j - v] + w);
21             int cnt = 0;
22             if(maxv == f[j])cnt += g[j];
23             if(maxv == f[j - v] + w)cnt += g[j - v];
24             f[j] = maxv;
25             g[j] = cnt % mod; 
26         }
27     }
28     
29     int res = 0;
30     for(int i = 1 ; i <= m ; i ++)res = max(res, f[i]);
31     
32     int cnt = 0;
33     for(int i = 1 ; i <= m ; i ++)
34         if(res == f[i])
35             cnt = (cnt + g[i]) % mod;
36     
37     cout << cnt << endl;
38     return 0;
39 }

有依赖的背包问题

重新定义状态$f[u][j]$，表示以$u$为根的子树中，总质量不超过$j$的方案。那么每一个子树可以当做是分组背包的一个组别，实质上是树形的分组背包问题。从根节点往下递归。不同的是我们这里不能用分组中背包的组合作为划分的依据，因为每一组中物品可能有$100$个，这样物品的组合有$2^{100}$种，显然无法存储。所以我们使用体积作为划分的依据，每一组中用体积$0 ~ m$划分为$m + 1$种组合。

acwing 10.有依赖的背包问题

https://www.acwing.com/problem/content/10/

 1 #include <iostream>
 2 #include <algorithm>
 3 #include <cstring>
 4 
 5 using namespace std;
 6 
 7 const int N = 110;
 8 int f[N][N];
 9 int e[N], ne[N], idx, h[N];
10 int v[N], w[N];
11 int n, m;
12 
13 void add(int a, int b)
14 {
15     e[idx ] = b , ne[idx] = h[a], h[a] = idx ++;
16 }
17 
18 void dfs(int u)
19 {
20     for(int i = h[u] ; ~i ; i = ne[i])//循环分组
21     {
22         int son = e[i];
23         dfs(son);
24         
25         for(int j = m - v[u] ; j >= 0 ; j --)//循环体积
26             for(int k = 0 ; k <= j ; k ++)//循环决策
27                 f[u][j] = max(f[u][j], f[u][j - k] + f[son][k]);
28     }
29     
30     for(int i = m ; i >= v[u] ; i --)f[u][i] = f[u][i - v[u]] + w[u];//选入第u个物品
31     for(int i = 0 ; i < v[u] ; i ++)f[u][i] = 0;//体积不够的无法选入
32 }
33 
34 int main(){
35     cin >> n >> m;
36     int root;
37     memset(h, -1, sizeof h);
38     for(int i = 1 ; i <= n ; i ++)
39     {
40         int p;
41         cin >> v[i] >> w[i] >> p;
42         if(p == -1)root = i;
43         else add(p, i);
44     }
45     
46     dfs(root);
47     
48     cout << f[root][m] << endl;
49     
50     return 0;
51 }

posted @ 2020-04-05 17:30 dzcixy 阅读(181) 评论(0) 收藏举报

刷新页面返回顶部

dzcixy

个人博客http://dzcixy.gitee.io/