组合数

①当参数范围较小的时候，并且有取模，可以直接通过递推式$C_{a}^{b}=C_{a - 1}^{b}+C_{a-1}^{b-1}$直接递推出来。（递推）

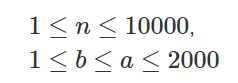
void init()
{
    for(int i = 0 ; i < N ; i ++)
        for(int j = 0 ; j <= i ; j ++)
            if(!j)c[i][j] = 1;
            else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;
}

②当参数范围较小，并且有取模，取模的是一个质数时，可以分别递推分子的阶乘和分母阶乘，分母用逆元递推。其中qmi为快速幂函数。（预处理）

 

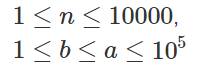
fact[0] = infact[0] = 1;
    for(int i = 1 ; i < N ; i ++)
    {
        fact[i] = (LL)fact[i - 1] * i % mod;
        infact[i] = (LL)infact[i - 1] * qmi(i, mod - 2, mod) % mod;
    }

③当参数范围变大时，并且有取模，可以使用Lucas定理求解组合数。（定理）

$C_{a}^{b}\equiv C_{a\;mod\;p}^{b\;mod\;p}\cdot C_{a/p}^{b/p}$

 

int C(int a, int b)
{
    int res = 1;
    for(int i = 1, j = a ; i <= b ; i ++, j --)
    {
        res = (LL)res * j % p;
        res = (LL)res * qmi(i, p - 2) % p;
    }
    return res;
}

int lucas(LL a, LL b)
{
    if(a < p && b < p)return C(a, b);
    else return (LL)C(a % p, b % p) * lucas(a / p, b / p) % p;
}

int main(){
    int n;
    cin >> n;
    while(n --)
    {
        LL a, b;
        cin >> a >> b >> p;
        cout << lucas(a, b) << endl;
    }
    return 0;
}

 

④当要求求组合数的确切值，并没有取模时，需要分解阶乘和质因数，最后用高精度相乘求出结果。(分解质因数)

 

int get(int n, int p)//获取阶乘中某个质因子的个数
{
    int res = 0;
    while(n)
    {
        res += n / p;
        n /= p;
    }
    return res;
}

void get_primes(int n)
{
    for(int i = 2 ; i <= n ; i ++)
    {
        if(!st[i])primes[cnt ++] = i;
        for(int j = 0 ; i * primes[j] <= n ; j ++)
        {
            st[i * primes[j]] = true;
            if(i % primes[j] == 0)break;
        }
    }
}

vector<int> mul(vector<int> a, int b)//高精度乘
{
    vector<int> c;
    int t = 0;
    for(int i = 0 ; i < a.size() ; i ++)
    {
        t += a[i] * b;
        c.push_back(t % 10);
        t /= 10;
    }
    
    while(t)
    {
        c.push_back(t % 10);
        t /= 10;
    }
    return c;
}

int main(){
    cin >> a >> b;
    
    get_primes(a);
    
    for(int i = 0 ; i < cnt ; i ++)
    {
        int p = primes[i];
        sum[i] = get(a, p) - get(b, p) - get(a - b, p);//sum存储每个质因子的个数
    }
    
    vector<int> res;
    res.push_back(1);
    for(int i = 0 ; i < cnt ; i ++)
        for(int j = 0 ; j < sum[i] ; j ++)
            res = mul(res, primes[i]);
           
    
     
    for(int i = res.size() - 1 ; i >= 0 ; i --)cout << res[i];
    puts(" ");
    return 0;
    
}