单源最短路建图，分层图

https://www.acwing.com/problem/content/905/

acwing 903.昂贵的聘礼

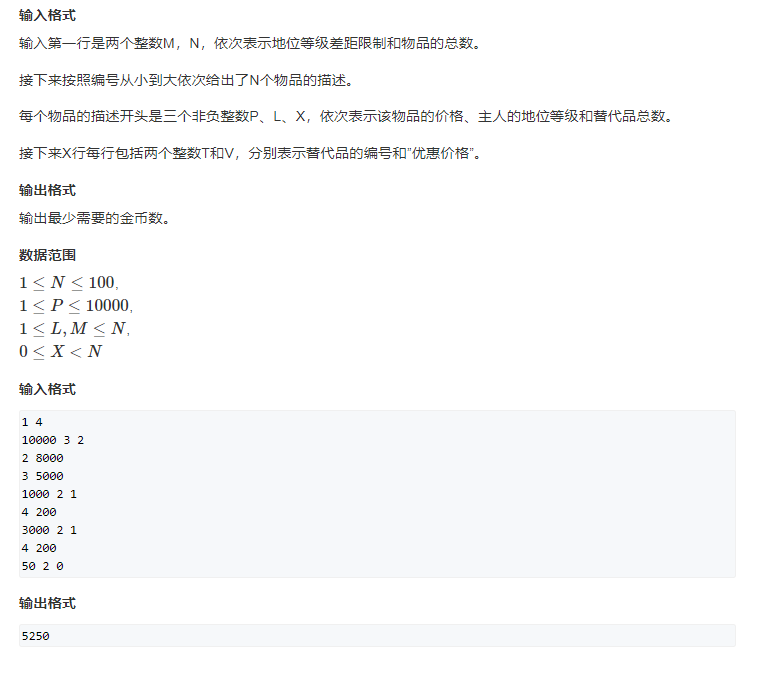
把每一个物品看作是一个点，此题是一定有解的，因为最坏的情况也是花费10000金币直接给酋长。所以这题将每个物品看作一个点，以替换的价值向替换的物品连边。就是一个最短路的问题。

不同的是，该题的物品是有等级划分的，也就是说要在一个等级区间内的物品才可以进行交易替换。所以我们要给最短路函数传入两个参数$up$和$down$,分别表示等级的上下界。然后以第一个物品的等级左右$m$为区间跑最短路算法取最小值。

还要注意的是，因为每个物品都可以直接购买，所以我们要建立一个虚拟源点0，指向每一个物品。

#include <iostream>
#include <algorithm>
#include <queue>
#include <cstring>

using namespace std;

const int N = 110, M = N * N, INF = 0x3f3f3f3f; 
int n, m;
int level[N];//存储等级的数组
int e[M], ne[M], w[M], h[N], idx;
int dis[N];
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

int spfa(int down, int up)
{
    memset(dis, 0x3f, sizeof dis);
    queue<int> q;
    q.push(0);
    st[0] = true;
    dis[0] = 0;
    
    while(q.size())
    {
        int t = q.front();
        q.pop();
        
        st[t] = false;
        
        for(int i = h[t] ; ~ i ; i = ne[i])
        {
            int j = e[i];
            if(level[j] <= up && level[j] >= down)
            {
                if(dis[j] > dis[t] + w[i])
                {
                    dis[j] = dis[t] + w[i];
                    if(!st[j])
                    {
                        q.push(j);
                        st[j] = true;
                    }
                }
            }
        }
    }
    return dis[1];
}



int main(){
    cin >> m >> n;
    
    memset(h, -1, sizeof h);
    for(int i = 1 ; i <= n ; i ++)
    {
        int price, cnt;
        cin >> price >> level[i] >> cnt;
        add(0, i, price);//每个物品都要有一个虚拟源点指向
        
        while(cnt --)
        {
            int id, cost;
            cin >> id >> cost;
            add(id, i, cost);//由该物品向可替换物品连边
        }
    }
    
    int ans = INF;
    for(int i = level[1] - m ; i <= level[1] ; i ++)ans = min(ans, spfa(i, i + m));//循环等级区间的左端点
    
    cout << ans << endl;
    return 0;
}

 

https://www.acwing.com/problem/content/1133/

acwing 1131.拯救大兵瑞恩

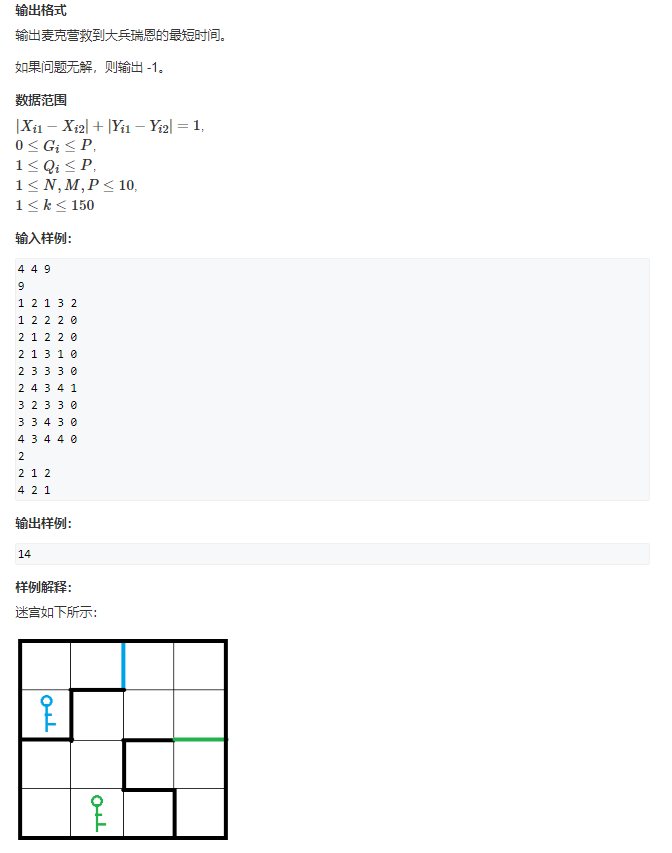
分层图。因为有门的存在需要有钥匙才可以过去，所以是需要有一维的参数是状态。考虑$dp$的思想，以$dis[x][y][state]$表示从起点走到$（x, y）$并且状态是state所花费的时间。由于本题捡起钥匙是不花费任何代价的，所以走到一个点有钥匙，就一定要将其拿起，,所以该点有钥匙的时候，很自然就能想到一个转移公式$dis[x][y][state | key] = dis[x][y][state]$。($ps:key$也是一个二进制数)。

而对于没有钥匙的情况，就是枚举上下左右四个方向，进行转移。

根据上面的分析，如果是有钥匙的转移，边权是0， 如果是四个方向的转移，边权为1，所以我们可以用双端队列，当边权为0加入队首，当边权为1，加入队尾。

另外，此为了方便起见，将图中的二维坐标映射为一维坐标，假设$n$为4， 即$（1， 1）$是1， $（1， 2）$是2，$（2， 1）$是5。这样就能将dis数组降为二维。

该题的图中有三种边，墙，无障碍，门。在读入时，将门建边，墙不建边（这样就等于无路可走），因为题目只读入墙和门，所以用一个$set$记录已经建过边的墙和门，剩下的都是属于无障碍，可以直接建边， 用一个$build$函数实现。

因为钥匙是从1开始，我们用二进制表示，就将钥匙的数映射少一位，从0开始。

#include <iostream>
#include <cstring>
#include <algorithm>
#include <deque>
#include <set>

#define x first
#define y second
using namespace std;

typedef pair<int,int> PII;


//对于一个n的图，每行的竖边有n - 1条，n条边就有n(n -1)条竖边，横边一样，并且还有双向边，所以总共有2 * 2 * n(n - 1)
//n为10带入有360，开400。一共最多有十把钥匙，用二进制的十位数表示。
const int N = 11, M = 400, P = 1 << 10;

int e[M], ne[M], w[M], h[N * N], idx;
int dis[N * N][P], g[N][N];
bool st[N * N][P];
int key[N * N];
set<PII> edges;
int n, m, k, p;

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

void build()
{
    int dx[4] = {0, 1, -1, 0}, dy[4] = {1, 0, 0, -1};
    
    for(int i = 1 ; i <= n ; i ++)
        for(int j = 1 ; j <= m ; j ++)
            for(int k = 0 ; k < 4 ; k ++)
            {
                int x = i + dx[k], y = j + dy[k];
                if(!x || !y || x > n || y > m)continue;
                int a = g[i][j], b = g[x][y];
                if(edges.count({a, b}) == 0)add(a, b, 0);//如果墙和门没建过，就是无障碍
            }
}

int bfs()
{
    memset(dis, 0x3f, sizeof dis);
    dis[1][0] = 0;
    
    deque<PII> q;
    q.push_back({1, 0});
    
    while(q.size())
    {
        PII t = q.front();
        q.pop_front();
        
        if(st[t.x][t.y])continue;
        st[t.x][t.y] = true;
        
        if(t.x == n * m)return dis[t.x][t.y];
        
        if(key[t.x])//该点有钥匙的时候
        {
            int state = t.y | key[t.x];
            if(dis[t.x][state] > dis[t.x][t.y])
            {
                dis[t.x][state] = dis[t.x][t.y];
                q.push_front({t.x, state});
            }
        }
        
        for(int i = h[t.x] ; ~ i ; i = ne[i])//枚举四个方向
        {
            int j = e[i];
            if(w[i] && !(t.y >> w[i] - 1 & 1))continue;//如果这条路是门，但没有钥匙
            if(dis[j][t.y] > dis[t.x][t.y] + 1)
            {
                dis[j][t.y] = dis[t.x][t.y] + 1;
                q.push_back({j, t.y});
            }
        }
    }
    return -1;
}

int main(){
    cin >> n >> m >> p >> k;
    
    for(int i = 1, t = 1 ; i <= n ; i ++)//映射一维坐标
        for(int j = 1 ; j <= m ; j ++)
            g[i][j] = t ++;
    
    memset(h, -1, sizeof h);
    while(k --)
    {
        int x1, x2, y1, y2, c;
        cin >> x1 >> y1 >> x2 >> y2 >> c;
        int a = g[x1][y1], b = g[x2][y2];
        edges.insert({a, b}), edges.insert({b, a});//记录墙和门
        if(c)add(a, b, c), add(b, a, c);//如果不是墙是门就建边
    }
    
    build();
    
    int s;
    cin >> s;
    while(s --)
    {
        int a, b, c;
        cin >> a >> b >> c;
        key[g[a][b]] |= 1 << c - 1;//该点有一个钥匙，坐标映射从0开始
    }
    
    
    cout << bfs() << endl;
    
    return 0;
}