迭代加深，剪枝

五大剪枝：

①优化搜索顺序：先搜答案数较小的分支，这样有很大概率能将后续的分支剪去

②排除等效冗余：例如1 2 3 4 要枚举这四个数的和，那么1 + 4和 2 + 3就只需要枚举一次就够了。

③可行性剪枝：在搜索过程中对当前状态进行检查，如果发现分支已经无法达到递归边界，就执行回溯。

④最优性剪枝：在搜索过程中对当前状态进行检查，如果发现分支已经比目前得知的最佳状态差，就执行回溯。

⑤记忆化：可以记录每个状态的搜索结果，在重复遍历一个状态时直接检索并返回。

 

https://www.acwing.com/activity/content/problem/content/1486/1/

acwing 166 数独

这题是81的数独且行，列，九宫格都有互斥关系，所以需要的状态很多，考虑使用二进制来表示数字的使用与否，用$row,col,cell$三个数组分别存储行，列，九宫格在这个点位所能使用的数字。

例如000000001就表示只有1可以使用。其次因为使用的是二进制来表示这个数，所以还要建立一个$map$来映射这个二进制数是十进制的什么数字。

这题的搜索空间很大，考虑优化搜索顺序，从分支较少的点开始进行填数，也就是可填的数字最少的点，所以我们还需要预处理一下所有二进制数中1的个数，用$ones$数组存储下来。

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 9, M = 1 << N;

int ones[M], map[M];
int row[N], col[N], cell[3][3];
char str[100];

void init()
{
    for(int i = 0 ; i < N ; i ++)row[i] = col[i] = (1 << N) - 1;
    for(int i = 0 ; i < 3 ; i ++)
        for(int j = 0 ; j < 3 ; j ++)
            cell[i][j] = (1 << N) - 1;
}

void draw(int x, int y, int t, bool is_set)
{
    if(is_set)str[x * N + y] = '1' + t;
    else str[x * N + y] = '.';
    
    int v = 1 << t;
    if(!is_set)v = -v;
    row[x] -= v;
    col[y] -= v;
    cell[x / 3][y / 3] -= v;
}

int lowbit(int x)
{
    return x & -x;
}

int get(int x, int y)
{
    return row[x] & col[y] & cell[x / 3][y / 3];
}

bool dfs(int cnt)
{
    if(!cnt)return true;
    
    int minv = 10;
    int x, y;
    for(int i = 0 ; i < N ; i ++)
        for(int j = 0 ; j < N ; j ++)
            if(str[i * N + j] == '.')
            {
                int state = get(i, j);
                if(ones[state] < minv)
                {
                    minv = ones[state];
                    x = i;
                    y = j;
                }
            }
    int state = get(x, y);
    for(int i = state ; i ; i -= lowbit(i))
    {
        int t = map[lowbit(i)];
        draw(x, y, t, true);
        if(dfs(cnt - 1))return true;
        draw(x, y, t, false);
    }
    
    return false;
    
}

int main(){
    for(int i = 0 ; i < N ; i ++)map[1 << i] = i;
    for(int i = 0 ; i < 1 << N ; i ++)
        for(int j = 0 ; j < N ; j ++)
            ones[i] += i >> j & 1;
    
    while(cin >> str, str[0] != 'e')
    {
        init();
        
        int cnt = 0;
        for(int i = 0, k = 0 ; i < N ; i ++)
            for(int j = 0 ; j < N ; j ++, k ++)
                if(str[k] != '.')
                {
                    int t = str[k] - '1';
                    draw(i, j, t, true);
                }
                else cnt ++;
        
        dfs(cnt);
        
        puts(str);
    }
    return 0;
}

 

 

迭代加深搜索：当搜索的答案树很深，但是答案在比较浅的位置时适合使用。

https://www.acwing.com/problem/content/172/

acwing 170 加成序列

按题目要求，序列可以为$1 \;2\; 4\; 8\; 16\; \cdot \cdot \cdot$每次倍增，所以最短的结果必然在比较浅层内，而搜索树又很大，所以考虑使用迭代加深，一层一层往下搜索。

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 110;
int path[N];
int n;

bool dfs(int u, int depth)
{
    if(u > depth)return false;
    if(path[u - 1] == n)return true;
    
    bool st[N] = {0};
    for(int i = u - 1 ; i >= 0 ; i --)
        for(int j = i ; j >= 0 ; j --)
        {
            int s = path[i] + path[j];
            if(st[s] || s <= path[u - 1] || s > n)continue;
            st[s] = true;
            path[u] = s;
            if(dfs(u + 1, depth))return true;;
        }
    return false;
}

int main(){
    while(cin >> n, n)
    {
        int depth = 1;
        path[0] = 1;
        while(!dfs(1, depth))depth ++;
        
        for(int i = 0 ; i < depth ; i ++)
            cout << path[i] << " ";
        cout << endl;
    }
    return 0;
}

 

 

https://www.acwing.com/problem/content/173/

acwing 171 送礼物

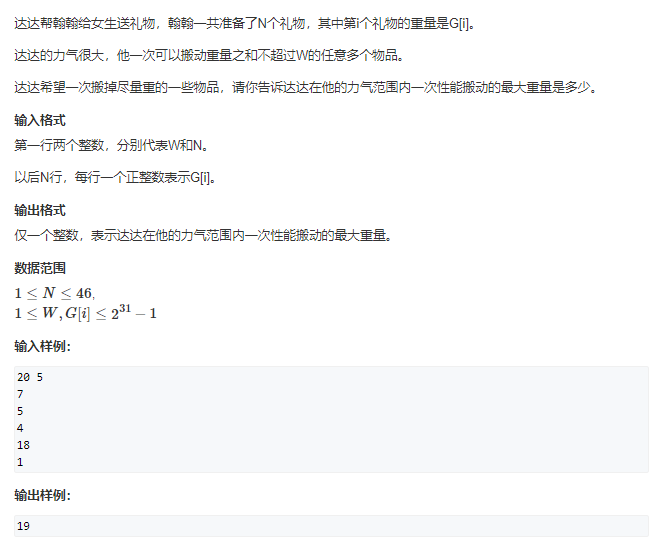
典型的双向深搜。对于这题来说，$M$的范围有$2^{31}$，$N$ 是 $46$，如果采用背包问题的求解，时间复杂度是$O（NM）$过大，考虑到$N$很小，所以可以用爆搜。

但是如果直接爆搜，复杂度有$2^{46}$。也是过大，所以考虑使用双向深搜，这样就可以吧复杂度降到$2^{\frac{N}{2}}+\frac{N}{2}2^{\frac{N}{2}}$。为了更均衡一下，可以使得$N = 25$，这样，复杂度就降的比较低。

 所以最后先爆搜前$\frac{n}{2} + 2$个部分，预处理出结果，剩下的部分再进行爆搜。

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

typedef long long LL;

const int N = 46;

int w[N], cnt = 1;
int weights[1 << 25];
int n, m;
int ans, k;

void dfs1(int u, int s)
{
    if(u == k)
    {
        weights[cnt ++] = s;
        return;
    }
    dfs1(u + 1, s);
    if((LL)s + w[u] <= m)dfs1(u + 1, s + w[u]);
}

void dfs2(int u, int s)
{
    if(u == n)
    {
        int l = 0, r = cnt - 1;
        while(l < r)
        {
            int mid = l + r + 1 >> 1;
            if((LL)s + weights[mid] <= m)l = mid;
            else r = mid - 1;
        }
        ans = max(ans, weights[l] + s);
        return;
    }
    dfs2(u + 1, s);
    if((LL)s + w[u] <= m)dfs2(u + 1, s + w[u]);
}

int main(){
    cin >> m >> n;
    
    for(int i = 0 ; i < n ; i ++)cin >> w[i];
    
    sort(w, w + n);
    reverse(w, w + n);
    
    k = n / 2 + 2;
    
    dfs1(0, 0);
    
    sort(weights, weights + cnt);
    cnt = unique(weights, weights + cnt) - weights;
    
    dfs2(k, 0);
    
    cout << ans << endl;
    return 0;
}