指数枚举，排列枚举，组合枚举以及n皇后问题

指数形枚举：即集合中的元素，选或者不选两种状态，$0$和$1$， 即集合的所有子集。例如$\left \{ 1,2 \right \}$集合中的子集有$\left \{  \right \}，\left \{ 1 \right \}，\left \{ 2 \right \}，\left \{ 1,2 \right \}$。

运用深搜进行指数型枚举，在挑选数字时，用一个状态$state$记录挑选的数字，从前往后枚举，当枚举到最后一位的后一位
的时候，输出。

#include <iostream>

using namespace std;

const int N = 20;

int a[N];
int n;

void dfs(int step, int state)
{
    if(step == n)//当枚举到最后一位的后一位，即代表前面n位都尝试过，输出
    {
        for(int i = 0 ; i < n ; i ++)//遍历状态
            if(state >> i & 1)//如果该数字的状态是选中就输出
                cout << i + 1 << " ";//由于step从0开始，数字从1开始，要加上偏移量
        cout << endl;
        return;//输出完务必return
    }
    dfs(step + 1, state);//对下一个数做决定，不选当前数
    dfs(step + 1, 1 << step | state);//对下一个数做决定，选当前数
}

int main(){
    cin >> n;
    
    dfs(0, 0);
    
    return 0;
}

 

组合型枚举：组合型枚举一般为从$n$个数中选择$m$个数，$m\leq n$。例如$\left \{ 1,2 ,3\right \}$中选$2$个数，有$\left \{ 1,2 \right \}，\left \{ 1,3 \right \}，\left \{ 2,3 \right \}$。

依旧是运用深搜枚举，同样用一个$state$记录被选数字，与指数型枚举不同的是：1.必须优先选择当前数字。2.当已经到最后一个数字的后一位时还没有选择满$m$个数字，要$return$。

#include <iostream>

using namespace std;

const int N = 25;

int a[N];
int n, m;

void dfs(int step, int state, int cnt)
{
    if(cnt == m)//当选满m个数字，输出数字
    {
        for(int i = 0 ; i < n ; i ++)
            if(state >> i & 1)
                cout << i + 1 << " ";
        cout << endl;
        return;//记得return
    }
    if(step == n)return;//如果到最后一位后一位还未满m个数字，return
    dfs(step + 1, 1 << step | state, cnt + 1);//优先选择当前数字的方案
    dfs(step + 1, state, cnt);//不选择当前数字的方案
    
}

int main(){
    cin >> n >> m;
    
    dfs(0, 0, 0);
    return 0;
}

 

排列型枚举：即$\left \{ 1,2 \right \}$与$\left \{ 2,1 \right \}$是不同的排列方案。

用深搜进行搜索，用一个$st$数组标记被选数字，用$a$数组存储被选数字。

#include <iostream>

using namespace std;

const int N = 10;

int a[N];
bool st[N];
int n;

void dfs(int step)
{
    if(step == n)
    {
        for(int i = 0 ; i < n ; i ++)
            cout << a[i] << " ";
        cout << endl;
        return;
    }
    for(int i = 1 ; i <= n ; i ++)//枚举1-9的数字
        if(!st[i])//如果没有用过
        {
            a[step] = i;//将该数组存储到a数组内
            st[i] = true;//标记该数字已经选过
            dfs(step + 1);//进行下一步
            st[i] = false;//回溯
        }
}

int main(){
    cin >> n;
    
    dfs(0);
    
    return 0;
}

 

$n$-皇后问题：$n$-皇后问题是指将 $n$ 个皇后放在 $n∗n$ 的国际象棋棋盘上，使得皇后不能相互攻击到，即任意两个皇后都不能处于同一行、同一列或同一斜线上。

我们使用深搜，用$step$代表一次步骤，即代表一行，对于每一行，枚举每一列，判断在该位置上的竖直方向，两个斜边方向上是否有皇后，没有就放下。

判断竖线上是否有皇后用一个$st$数组即可，对于斜边，我们知道，对于处在同一条斜边上的（列数-行数）和 （列数+ 行数）的数值是相同的。

 

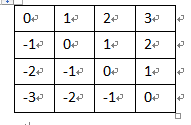
 例如对于（列数-行数）的值如是。

#include <iostream>

using namespace std;

char g[20][20];
bool st[20], a[20], b[20];
int n;

void dfs(int step)
{
    if(step == n)
    {
        for(int i = 0 ; i < n ; i ++)cout << g[i] << endl;
        puts(" ");
        return;
    }
    for(int i = 0 ; i < n ; i ++)
        if(!st[i] && !a[i + step] && !b[i - step + n])//竖直方向和两斜边都没有皇后可以攻击到
        {
            g[step][i] = 'Q';//放下
            st[i] = a[i + step] = b[i - step + n] = true;
            dfs(step + 1);
            g[step][i] = '.';//回溯
            st[i] = a[i + step] = b[i - step + n] = false;
        }
}

int main(){
    cin >> n;
    for(int i = 0 ; i < n ; i ++)
        for(int j = 0 ; j < n ; j ++)g[i][j] = '.';
    
    dfs(0);
    
    return 0;
}