二分图

二分图又称作二部图，是图论中的一种特殊模型。 设$G=(V,E)$是一个无向图，如果顶点$V$可分割为两个互不相交的子集$(A,B)$，并且图中的每条边$（i，j）$所关联的两个顶点$i$和$j$分别属于这两个不同的顶点集$(i  \ in \  A,j \  in  \ B)$，则称图$G$为一个二分图。

1.二分图的判定：不存在奇数环或染色法不生产矛盾。

关押罪犯

 

 

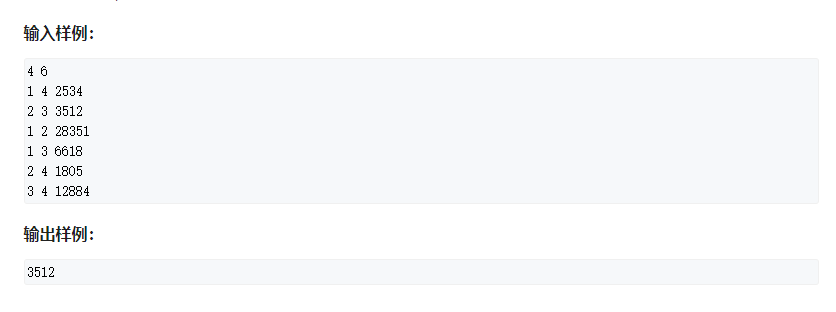
 二分 + 二分图判定。

对于一个二分点$mid$，如果仇恨值大于$mid$的所有罪犯在二分图的两个集合内（集合内部没有边），$mid$就是合法的。$mid$是合法的，那么大于$mid$的所有点能构成二分图，当$mid$取更大值的时候也一定能构成二分图（二分图去掉一些边还是二分图）。所以只需要判断大于mid的关系是否构成二分图。

如果$check(mid)$成功，说明$mid$可行，大于$mid$的也可行，答案在左边，$r = mid$,反之$l = mid + 1$。

本题的边界0不需要特判，因为$mid = 0$的时候，也是满足二分图的判定条件。

代码：

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>

using namespace std;

const int N = 20010, M = 200010;

int n, m;
int h[N], e[M], w[M], ne[M], idx;
int color[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}


bool dfs(int u, int c, int mid)
{
    color[u] = c;
    for(int i = h[u] ; ~i ; i = ne[i])
    {
        int j = e[i];
        if(w[i] <= mid)continue;//小于mid的边就不用管
        if(color[j])
        {
            if(color[j] == c)return false;
        }
        else if(!dfs(j, 3 - c, mid))return false;
    }
    return true;
}

bool check(int mid)
{
    memset(color, 0, sizeof color);
    for (int i = 1; i <= n; i ++ )
        if (!color[i])//未染色就染色
            if (!dfs(i, 1, mid))
                return false;
    return true;
}

int main()
{
    scanf("%d%d", &n, &m);
    memset(h, -1, sizeof h);

    while (m -- )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c), add(b, a, c);
    }

    int l = 0, r = 1e9;
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;
        else l = mid + 1;
    }

    printf("%d\n", r);

    return 0;
}

 

 

 

 

 二分图的最大匹配

匈牙利算法：

①匹配：对于二分图，匹配指一组边，每两条边之间没有公共点。

②最大匹配：边数最多的匹配。

③ 匹配点：匹配中的点。

④非匹配点：不在匹配当中的点。

⑤增广路径：从非匹配点->非匹配边->匹配边->非匹配边->匹配边->非匹配边->非匹配点。从非匹配点走，最后到非匹配点。

最大匹配 <->不存在增广路径

棋盘覆盖

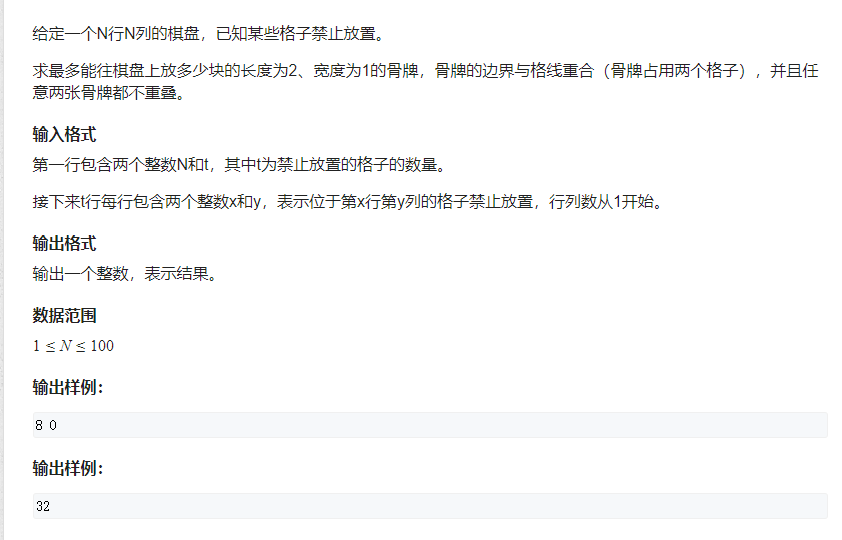
可以将棋盘的每一个格子看做一个点，相邻的格子看做一条边，问题就变成了最多选多少条边，使得边没有公共点， 即找最大匹配。将格子的横纵坐标相加的值为奇数或偶数分为两边，可以得知是一个二分图，题意就变成求二分图的最大匹配问题。

代码：

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>

#define x first
#define y second

using namespace std;

typedef pair<int, int> PII;

const int N = 110;

bool g[N][N], st[N][N];
PII match[N][N];
int n, m;
int dx[4] = {1, 0, -1, 0}, dy[4] = {0, 1, 0, -1};


bool find(int x, int y)
{
    for(int i = 0 ; i < 4 ; i ++)
    {
        int a = x + dx[i], b = y + dy[i];
        if(a < 1 || b < 1 || a > n || b > n)continue;
        if(st[a][b] || g[a][b])continue;
        st[a][b] = true;
        PII t = match[a][b];
        if(t.x == -1 || find(t.x, t.y))
        {
            match[a][b] = {x, y};
            return true;
        }
    }
    return false;
}

int main(){
    scanf("%d%d", &n, &m);
    
    while(m --)
    {
        int x, y;
        scanf("%d%d", &x, &y);
        g[x][y] = true;
    }
    
    memset(match, -1, sizeof match);
    
    int res = 0;
    for(int i = 1 ; i <= n ; i ++)
        for(int j = 1 ; j <= n ; j ++)
            if((j + i) % 2 && !g[i][j])//奇数点偶数点对称，选一种就可以
            {
                memset(st, 0, sizeof st);
                if(find(i, j))res ++;//能找到匹配就加上
            }
    
    printf("%d\n", res);
    return 0;
}

 

 

 

 

最小点覆盖：每一条边至少有一个点被选出，选出的点数最少

在二分图中，最小点覆盖 = 最大匹配数。

机器任务

 

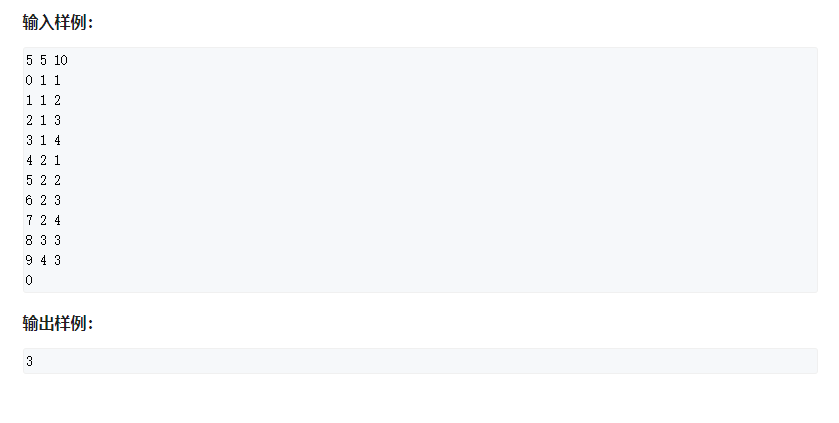
 可以将题目中的a[i]向b[i]连一条边，转换成，a[i]到b[i]的边上至少要有一个被选点，求最小点覆盖。

代码：

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>

using namespace std;

const int N = 110;
int match[N];
bool st[N], g[N][N];
int n, m, k;

bool find(int x)
{
    for(int i = 1 ; i < m ; i ++)
        if(!st[i] && g[x][i])
        {
            st[i] = true;
            if(match[i] == -1 || find(match[i]))
            {
                match[i] = x;
                return true;
            }
        }
    return false;
}

int main(){
    while(cin >> n, n)
    {
        cin >> m >> k;
        memset(match, -1, sizeof match);
        memset(g, 0, sizeof g);
        
        while(k --)
        {
            int t, a, b;
            cin >> t >> a >> b;
            if(!a || !b)continue;//刚开始是0就直接完成，无需记录
            g[a][b] = true;
        }
        
        int res = 0;
        for(int i = 1 ; i < n ; i ++)
        {
            memset(st, 0, sizeof st);
            if(find(i))res ++;
        }
        
        
        cout << res << endl;
    }
    
 
    return 0;
}

 

 

 

 

最大独立集：从图中选最多的点，使得选出的点之间（作为一个集合内部）无边。

最大团：从图中选最多的点，使得选出的点之间（作为一个集合内部）都有边。

在二分图中 求最大独立集<->先求去掉最少的点，将所有边破坏<->先求最小点覆盖<->先求最大匹配。

所以最大独立集 = 总数 - 最大匹配。

 

骑士放置

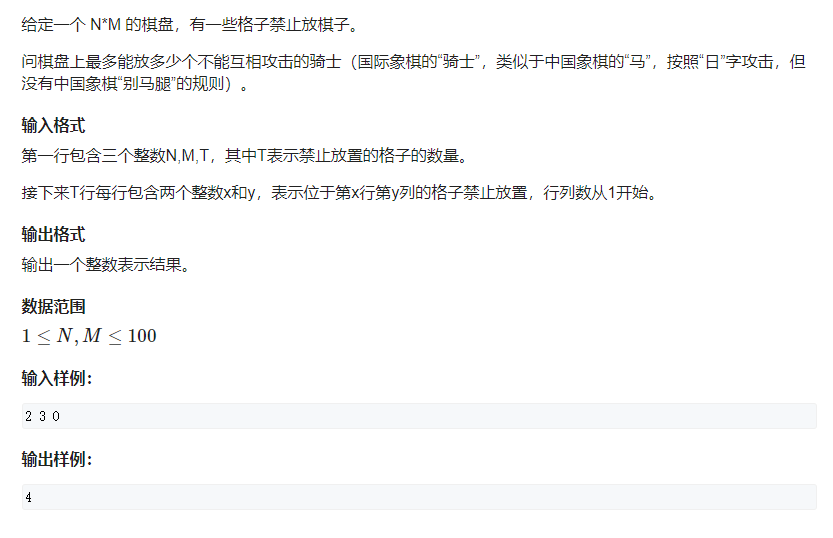
这题也可以用状压DP做。

将每个格子看做一个点，关系看做一条边，题意就变成选取最多的点，使每个点之间无边，格子的总数减去最大匹配和不能填的点数，即为答案。

 代码：

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>

#define x first
#define y second

using namespace std;

typedef pair<int,int> PII;

const int N = 110;

PII match[N][N];
bool st[N][N], g[N][N];
int n, m, k;

int dx[8] = {-1, 1, 2, 2, 1, -1, -2, -2};
int dy[8] = {2, 2, 1, -1, -2, -2, -1, 1};

bool find(int x, int y)
{
    for(int i = 0 ; i < 8 ; i ++)
    {
        int a = x + dx[i], b = y + dy[i];
        if(a < 1 || b < 1 || a > n || b > m)continue;
        if(g[a][b] || st[a][b])continue;
        st[a][b] = true;
        PII t = match[a][b];
        if(t.x == 0 || find(t.x, t.y))
        {
            match[a][b] = {x, y};
            return true;
        }
    }
    return false;
}

int main(){
    cin >> n >> m >> k;
    
    for(int i = 0 ; i < k ; i ++)//下面需要用到k，不能用while(k --)
    {
        int x, y;
        cin >> x >> y;
        g[x][y] = true;
    }
    
    int res = 0;
    for(int i = 1 ; i <= n ; i ++)
        for(int j = 1 ; j <= m ; j ++)
        if((i + j) % 2 && !g[i][j])
        {
            memset(st, 0, sizeof st);
            if(find(i, j))res ++;
        }
    
    cout << n * m - k - res  << endl;
    return 0;
}

 

二分图的最小路径点覆盖：用最少的互不相交的路径将所有点覆盖

最小路径点覆盖 = 总点数- 最大匹配数。

最小路径重复点覆盖：用最少的边将所有点覆盖，可以相交，可以重边。

①先做一次传递闭包。

②做最小路径点覆盖。