Trie树

　　Trie树是一种前缀树，一种高效存储和查询字符串的数据结构，用来处理字符串前缀的出现问题，或者异或对等问题。

例如我们有字符串：abc,ac,ad,ac,ba,bd,bad,cad,cb,da,dab。要在这些字符串中找出ac这个字符串的个数。第一个想法就是暴力搜索，用目标串去和每一个字符串比较，用一个ans存储答案。显然暴力的做法在字符串数量变多的情况下是会超时的。所以我们这时候想到用trie树。

　　一般用到trie树的题目，要么都是小写字母，或者都是大写字母，或者都是数字，并且字符的数量不会太多。

一：求字符串出现次数

 

对于上面的这个题目，首先考虑建树的过程，我们是要找出在字符串集合里某个字符创出现的个数，用一个cnt数组来记录其出现的个数。在一个字符串的结束位置，将cnt数组加1。如下：

void insert(char s[]){
    int p = 0;
    for(int i = 0 ; s[i] ; i++){
        int u = s[i]-'a';
        if(!t[p][u])t[p][u] = ++idx;
        p = t[p][u];
    }
    cnt[p]++;
}

由于我们用一个idx来作为每一个字符串的标记，所以不同的字符串的标记是唯一的。所以每个字符串结束时候的cnt就是该字符串出现的次数。

接着是查找过程。我们依旧从p = 0根节点开始，依次跳转到该字符串的下一个字符的位置上，如果下一个字符的位置不存在为0，那么说明这个字符串在所有字符串集合里面都不存在，反之，这个字符串存在，结束时候的cnt就是该字符串出现的次数。代码如下：

int query(char s[]){
    int p = 0;
    for(int i = 0; s[i]; i ++){
        int u = s[i]-'a';
        if(!t[p][u])return false;
        else p = t[p][u];
    }
    return cnt[p];
}

 

 完整代码 :

 

#include <iostream>
#include <cstdio>

using namespace std;

const int N = 1e6+10;

int t[N][26],idx,cnt[N];
char str[N];

void insert(char s[]){
    int p = 0;
    for(int i = 0 ; s[i] ; i++){
        int u = s[i] - 'a';
        if(!t[p][u])t[p][u] = ++ idx;//如果是idx++，会有0，会和初始化的0混在一起导致错误
        p = t[p][u];
    }
    cnt[p]++;
}

int query(char s[]){
    int p = 0;
    for(int i = 0 ; s[i] ; i ++){
        int u = s[i]- 'a';
        if(!t[p][u])return false;
        else p = t[p][u];
    }
    return cnt[p];
}
int main(){
    int m ;
    cin >> m;
    while(m--){
        char c[2];
        scanf("%s%s", c, str);
        if(c[0] == 'I')insert(str);
        else cout << query(str) << endl;
    }
    return 0;
}

 

 

 

 

 如果是求前缀出现的次数，只需要再每次转换节点的后面cnt数组加1就可。如下:

void insert(char s[])
{
    int p = 0;
    for(int i = 0 ; s[i] ; i ++)
    {
        int u = s[i] - 'a';
        if(!t[p][u])t[p][u] = ++ idx ;
        p = t[p][u];
        cnt[p] ++;
    }
}

 

 二：求该字符集合内的字符串作为前缀在模式字符里面出现的次数

 

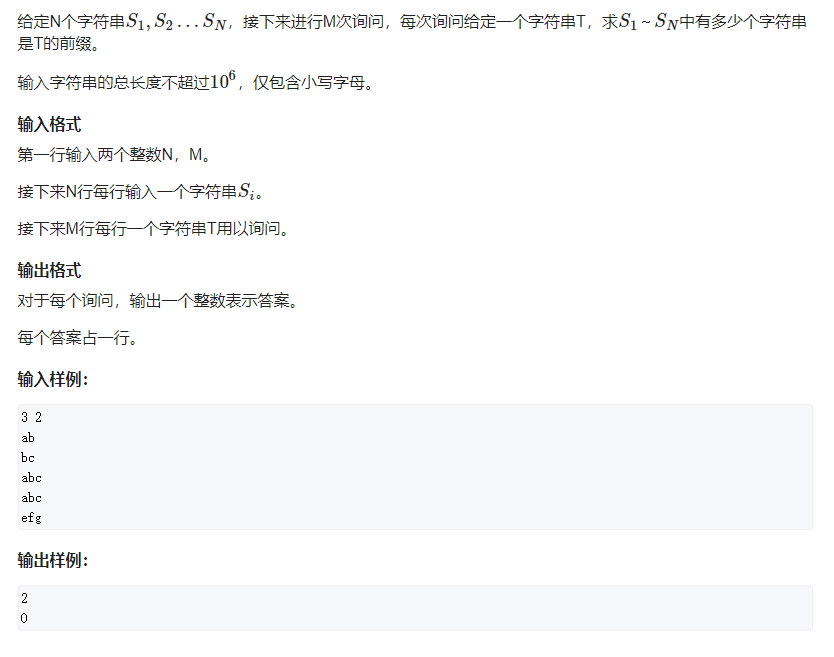
 建树并无差别，但是查询的时候需要在trie树上跳转，只要当前的模式字符串还没结束，就将沿途中的所有cnt数组的值加起来。

完整代码：

 

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 1e6+10;
int t[N][26], cnt[N], idx;

void insert(char s[])
{
    int p = 0;
    for(int i = 0 ; s[i] ; i ++)
    {
        int u = s[i] - 'a';
        if(!t[p][u])t[p][u] = ++ idx ;
        p = t[p][u];
    }
    cnt[p] ++;
}

int query(char s[])
{
    int p = 0, ans = 0;
    for(int i = 0 ; i < strlen(s) ; i ++)
    {
        int u = s[i] - 'a';
        p = t[p][u];
        if(p == 0)
            return ans;
        ans += cnt[p];
    }
    return ans;

}


int main(){
    int n, m;
    cin >> n >> m;
    while(n --)
    {
        char str[1000010];
        cin >> str;
        insert(str);
    }

    while(m --)
    {
           char str[1000010];
           cin >> str;
           cout << query(str) << endl;
    }
    return 0;

 

 

三：求最大异或对

 

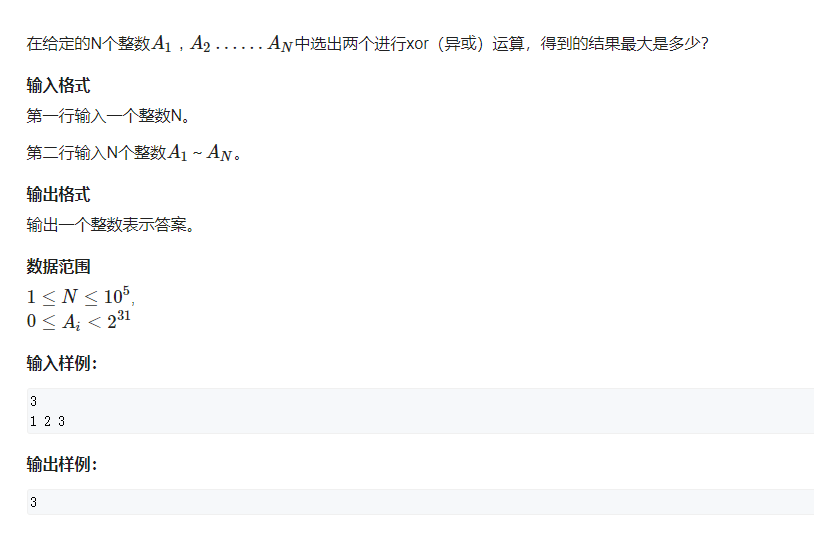
 求最大的异或对，想法是对于当前的一个数，我们将其拆分为二进制的数，如1就是1,2是10，因为最大的数是2^31，所以我们从最大的一位看起，每次都找和目标数异或为1的方向走，如果只有一条路，就只能沿这条路走。最终获得的数就是和当前数异或最大的数。

完整代码：

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 31, M = 1e5+10;;

int t[M * 31][2];
int a[M];
int idx;

void insert(int x)
{
    int p = 0;
    for(int i = 30 ; i >= 0 ; i --)
    {
        int u = x >> i & 1;
        if(!t[p][u])t[p][u] = ++ idx;
        p = t[p][u];
    }
}

int query(int x)
{
    int p = 0, res = 0;
    for(int i = 30 ; i >= 0 ; i --)//从最高位开始走
    {
        int u = x >> i & 1;
        if(t[p][!u])
        {
            p = t[p][!u];
            res = res * 2 + !u;//如果往这条路走，就将数*2在加上当前的数字
        }
        else
        {
            p = t[p][u];
            res = res * 2 + u;
        }
    }
    return res;
}

int main(){
    int n;
    cin >> n;
    for(int i = 0 ; i < n ; i ++)cin >> a[i];
    
    int ans = 0;
    for(int i = 0 ; i < n ; i ++)
    {
        insert(a[i]);//先插入在查询，防止第一次是空树无法查询出错，并且和自己的异或为0，不影响结果
        int t = query(a[i]);//t就是我们找到的配对
        ans = max(ans, a[i] ^ t);
    }
    cout << ans << endl;
    return 0;
}