2024.5 做题记录

2024.5 做题记录

[Violet] 天使玩偶

显然发现我们需要在时间轴上进行 cdq 分治，然后统计答案。

问题在于这个绝对值不好维护，需要进行转化。如果我们钦定这个点最近的点在它的左下方，那么绝对值就可以化为 \(dis(A,B)=(A_x-B_x)+(A_y-B_y)=(A_x+A_y)-(B_x+B_y)\)。显然前面的括号是定值，那么我们维护 \(B_x+B_y\) 的最大值即可。这个可以用树状数组简单做。

但是显然我们最后的答案不一定在左下方，还可能在其他四个方向。那么我们每次做完 cdq 就把整个坐标系旋转 \(90\degree\)，然后再次 cdq 即可。

[CTSC2018] 混合果汁

首先发现题目中有最小值最大的含义，可以想到二分。我们二分这个最小值，那么接下来我们就考虑买 \(d_i\ge mid\) 的果汁。此时再利用贪心，由于选价格小的一定更优，所以我们再按 \(p_i\) 排序依次选。此时会出现三种情况：钱没有花完就达到了体积要求、钱花完了没有达到体积要求、所有果汁买完了也达不到体积要求。

对于第一种情况我们增加最小值，否则减少最小值。但是这样做 check 的复杂度似乎较高。

考虑到朴素的二分时间主要花费在 check 上，那我们考虑缩小 check 的时间。首先对于第三种情况，我们可以十分简单的利用前缀和求解。同时，第二种情况的另一种表述就是 “达到体积要求的钱数大于当前钱数”，那么我们只需要再维护 “达到体积要求的最小钱数” 即可。

考虑使用线段树，以 \(d_i\) 为下标，存储总体积之和和价格之和。那么前缀和便可以解决。现在考虑怎样在线段树上求 “达到体积要求的最小钱数”，我们可以在线段树上二分，以类似于查找排名的方式求解。

现在时间复杂度就是 \(O(n\log^2 n)\)，做 \(m\) 次操作的复杂度就是 \(O(n^2\log^2 n)\)，显然过不去。

这时候就可以考虑整体二分，把查询放一块处理，时间复杂度就变成 \(O(n\log ^2 n)\) 了，可以通过。

[SCOI2007] 蜥蜴

首先我们肯定想到是从一个柱子向另一个能跳的柱子连边，但是这样下来是错误的。

我们考虑到这张图的权值在点上，因此考虑拆点，将每一个点拆成入点和出点，这两个点之间的容量就是柱子高度。而对于两个点之间，将第一个点的出点与第二个点的入点连边，容量为 \(\infty\)。

接下来我们考虑源点和汇点。首先源点应该是每个蟋蟀在的柱子，但是这样会有多个源点，因此建立超级源点；同理，所有边框外的部分都是汇点，因此建立超级汇点。

由于每个柱子上只能放一只蟋蟀，因此超级源点到每个汇点的容量是 \(1\)。

最后我们直接跑最大流即可，答案需要用总蟋蟀数减去最大流流量。

士兵占领

首先看到方格问题，直接考虑连 \(x\to y\) 的边。

接下来我们发现题目要求的是最小值，由于我们只会最大流，因此这个最小值显然是做不了的。考虑转化，即求出空出的格子数量的最大值，这样我们就可以使用最大流了。

那么既然这样我们就要求出每一行每一列空出的格子数 \(r'_i,c'_i\)。接着我们建立超级源点，从源点到每一个 \(x\) 连容量 \(r'_x\) 的边；建立超级汇点，从每一个 \(y\) 向汇点连容量为 \(c'_i\)​ 的边。

那么既然这样我们上面提到的 \(x\to y\) 的容量自然就是 \(1\) 了。于是我们跑最大流，然后用 \(nm-k\)​ 把最大流流量减去即可。

Upd：显然用上下界网络流也可以简单来做，使用有源汇上下界最小费用可行流即可。

[HNOI2007] 紧急疏散

这个题你的建图很容易假掉，然后这个题的数据还特别水，所以你的假做法大概能拿 \(50\sim 90\) 不等。

首先这道题是求出所有人撤离的最短时间，显然可以想到二分答案。我们假设当前要检查 \(mid\)，那么我们的门就有了时间限制。

既然这样，我们就可以采用按照时间拆点的方式来做。我们将每一个门拆成第 \(1,2,\cdots,mid\) 秒的门，接下来我们考虑连边。

首先建立超级源点，给所有空地连容量 \(1\) 的边，这表示每一块空地上有一个人。

然后我们计算出每一个空地到每一扇门的距离（可以从门开始用 BFS 求解），对于每一块空地，向任意一扇门的对应所用时间连边，容量为 \(1\)。

最后建立超级汇点，每一扇门向汇点连容量 \(1\) 的边，因为一扇门每次最多进一个人。

但是这样会有一个问题，尽管一扇门每次最多进一个人，但是先来的人可以等，然后再进门。也就是说门的时间也应该是变化的。因此将每一扇门的每个时刻向下一个时刻连边，容量为 \(\infty\)。

然后我们直接跑最大流就可以求出有多少人逃离了。

[SCOI2012] 奇怪的游戏

首先看到这个时间就知道肯定是二分答案。

由于这是棋盘问题且格子之间有影响，考虑黑白染色。假设黑色格子总数为 \(b\)，权值和为 \(B\)；白色格子总数为 \(w\)，权值和为 \(W\)。同时设 \(x\) 为最后变成的数，那么此时我们会有如下式子：

\[bx-B=wx-W \]

由于黑白格子总是同时染色，因此操作总次数应当相等，所以可以得到上式。接下来变形为：

\[x=\frac{B-W}{b-w} \]

那么此时我们分类讨论一下。

当 \(b-w=0\) 时：

显然此时我们无法直接求出 \(x\)，那我们就用二分。接下来考虑 check 函数。

由于黑白染色，所以先考虑从黑格向白格连边，容量为 \(\infty\)。然后建立超级源点 \(S\)，连向所有黑格 \((i,j)\)，容量为当前 \(x-a(i,j)\)，同时将这一部分容量累加记作 \(sum\)。同时建立超级汇点 \(T\)，所有白格 \((i,j)\) 连向汇点，容量为 \(x-a(i,j)\)。

然后我们跑最大流，如果流量等于 \(sum\)，说明整张图跑满了，也就是说每个数都能变成 \(x\)。

最后一定注意 \(x\) 不是答案，\(bx-B\) 才是答案。

当 \(b-w\ne 0\) 时：

显然可以直接求出 \(x\)，但这个 \(x\) 不一定合法，所以我们再用二分的 check 函数检查一下即可。

[国家集训队] 人员雇佣

这道题唯一的教训：网络流建图不要 YY，要有正确性。

我们首先将答案设置为 \(\sum\limits_{i=1}^n\sum\limits_{j=1}^nE_{i,j}\)，然后看怎样可以让损失的钱最少。容易想到是求最小割。

首先我们可以很容易的想到如下的东西：建立超级源点和超级汇点，从超级源点向每个点连容量 \(a_i\) 的边，从每个点向超级汇点连容量 \(\sum\limits_{j=1}^nE_{j,i}\) 的边。这样就代表该点去对面时，会对剩下的人产生 \(\sum\limits_{j=1}^nE_{j,i}\) 的影响，而来到我们公司则需要花 \(a_i\) 元。

那么这样我们就可以将超级源点看做对面公司，超级汇点看做我们公司。接下来考虑如何连剩下的边。

我们发现上面连的 \(\sum\limits_{j=1}^nE_{j,i}\) 只是计算了其他点的损失，但是这个点自己的损失却还没有计算。考虑如果这个点不去对面，会给出 \(E_{i,j}\) 的贡献；而如果去了对面，会给出 \(-E_{i,j}\) 的贡献。因此实际上一个点去对面所造成的差是 \(2E_{i,j}\)。

换句话说，如果一个点走了，它本身的贡献会从 \(E_{i,j}\) 变为 \(-E_{i,j}\)；而对于其他点，贡献只是从 \(E_{j,i}\) 变为了 \(0\)，并不会扣除贡献。

那么这样我们就可以直接求最小割了。

为什么不能使用类似 [国家集训队] happiness 的思路呢？

很简单：那道题目中走掉一个人或两个人对于答案的影响一致；而对于这道题，走一个人或两个人对于答案的影响是不同的。

[BZOJ3158] 千钧一发

首先让我们仔细观察题目中的性质，然后不难发现这样两条性质：

• 对于两个偶数，一定满足条件 \(2\)。
• 对于两个奇数，一定满足条件 \(1\)。

第二条的证明如下：

显然一个完全平方数 \(k^2\)，一定有 \(k^2\equiv 0/1\pmod{4}\)。其中当 \(k\) 为偶数时余数为 \(0\)，否则余数为 \(1\)。

现在考虑两个奇数 \(p,q\)，首先一定有 \(p^2\equiv 1\pmod 4,q^2\equiv 1\pmod 4\)，那么相加得 \(p^2+q^2\equiv 2\pmod 4\)。而上面我们已经说明一个平方数模 \(4\) 只能余 \(0,1\)，因此命题得证。

于是我们将 \(a_i\) 按照奇数和偶数分开，建立二分图。从 \(s\) 向奇数的点连 \(b_i\)，从偶数的点向 \(t\) 连 \(b_i\)。然后接下来我们暴力判断两部分之间是否能放在同一个集合里，如果不能就连一条 \(\infty\) 的边。

现在我们发现，要去掉的就是一个最小割，因此我们直接求最小割然后用 \(\sum\limits_{i=1}^nb_i\) 减去最小割容量即可。

[HNOI2013] 切糕

其实由这道题延伸出来了一种网络流模型，名字就叫切糕模型。具体内容如下：

题意：给出 \(n\) 个变量 \(x_i\)，其中每个变量的取值范围是 \([1,m]\)。对于一个变量 \(x_i\)，取 \(j\) 的代价为 \(a_{i,j}\)。同时，给出若干限制条件 \((u,v,w)\)，表示 \(x_u-x_v\le w\) （或 \(x_u-x_v\ge w\)）。

请求出一种合法的赋值方案，使得代价总和最小。

首先我们考虑拆点，将每一个变量拆成 \(p_{i,1},p_{i,2}\cdots p_{i,m},p_{i,m+1}\)，就是表示每个点分别选 \([1,m]\) 的情况。

现在我们考虑连边，首先要建出 \(n\) 条链，为 \(S\to p_{i,1}\to p_{i,2}\to\cdots\to p_{i,m}\to T\)。其中 \(p_{i,j}\to p_{i,j+1}\) 的容量就是 \(a_{i,j}\)，同时 \(S\to p_{i,1}\) 的容量就是 \(\infty\)。

这样我们断掉 \(p_{i,j}\to p_{i,j+1}\) 的边，实际的意义就是让 \(x_i=j\)。接下来考虑如何描述限制条件。

我们以 \(x_u-x_v\ge w\) 举例，此时我们直接连 \(p_{v,i}\to p_{u,i+w}\)，容量为 \(\infty\)。考虑这样做的实际含义，当我们断掉 \(p_{v,i}\to p_{v,i+1}\)，也就是 \(x_v=i\) 时，对于所有的 \(p_{u,j},j\le i+k\) 都应该会被划到左边源点的集合，因此在 \(u\) 那条链上断掉的边一定是在 \(p_{u,i+k}\) 之后，因此就满足了限制条件。

上面这一部分就是切糕模型的基本思路，现在回到这道题，我们发现不同的地方只在于限制条件变为了 \(|f_u-f_v|\le D\)，显然这个式子在上面的模型中是对称的，因此我们就可以将它看做是 \(f_u-f_v\le D\)，于是就是切糕模型的板子了。

Other Saying：

在 [RC-02] 开门大吉 中，这样普通的建图方式无法通过。考虑下图的情况：

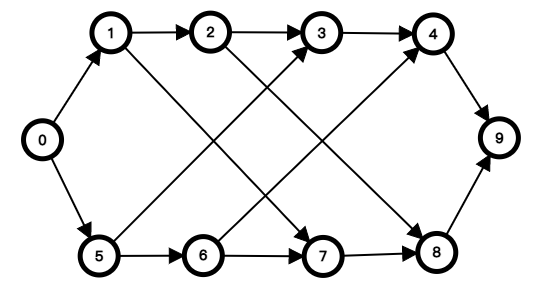
显然此时没有正确解法，但是我们真的去跑最小割会发现我们割掉了 \(1\to2,3\to4,5\to6,7\to8\) 然后求出了一个错误的答案。

出现这种现象的原因很简单，我们每个链上割了不止一条边，这样肯定就不符合上面所说的了。

解决方法也很简单：我们对于每一条边再连一条 \(p_{i,j}\to p_{i,j-1}\) 的容量为 \(\infty\) 的边。这样如果在一条边上有两条割边，我们依然能从 \(S\) 走到 \(T\)，这样显然就不对了。

但是本题没有这个限制。

[AHOI2009] 最小割

这道题就是让我们求一条边时最小割的可行性和必要性。

首先让我们先证明一个东西：最小割上的边在最大流上一定满流。

首先回到我们的最后一次增广，此时 \(s,t\) 还是有路径的。而当最后一条增广路被增广后，\(s,t\) 就不再联通。因此，这条增广路上的所有满流的边就可能会是最小割上的边。由于增广顺序不定，因此所有满流的边才有可能是最大流。

然后接下来我们再探究可行性和必要性的条件。

首先先看可行性，一个条件当然是上面提到的满流。另一方面，我们考虑一条边 \(u\to v\)，如果它在残量网络中仍然联通，那么就说明我们即使断掉这条边也不能将图割开，因此不会更优，所以最小割里一定没有这种边。

于是，我们就可以得到一条边在最小割中可行的充要条件：

1. 满流
2. 在残量网络中 \(u\) 无法到达 \(v\)。

接下来我们来看必要性。首先还是满流。其次我们考虑必要性的实质，也就是如果这条边不断，别的边就算全断也没法将图割开。因此这条边就是 \(s\to t\) 路径上的把守，考虑在残量网络上找，我们发现在残量网络上，如果一条边 \(u,v\)，满足 \(s\) 可以到达 \(u\) 且 \(v\) 可以到达 \(t\)，那么 \(u\to v\) 就是必须要割掉的边。

因此，一条边在最小割中必要的充要条件为：

1. 满流
2. \(s\) 可以到达 \(u\) 且 \(v\) 可以到达 \(t\)。

Tips：容易发现必要性的第二条一定满足可行性的第二条。

那么接下来我们考虑如何求解，首先第一个条件都是好求的，直接跑最小割看剩余容量。然后是判断联通。这里我们考虑使用强连通分量，直接判断两个点是否在同一强连通分量内就可以判断是否有路径可达。因此 Dinic 完再跑一遍 Tarjan 即可。

[SDOI2016] 数字配对

看到价值前提下最多的配对数，想到最大费用最大流。

我们首先对于每一个 \(a_i\) 分解质因数，设每个质因数的指数之和为 \(cnt_i\)。那么我们题目中的条件就可以转化为：\(a_i\) 是 \(a_j\) 的倍数且 \(cnt_i=cnt_j+1\)。

那么此时我们就考虑将 \(cnt_i\) 按照奇偶分组，然后转化成二分图问题求解。现在我们暴力枚举左部点和右部点，只要符合上述条件就从左部点向右部点连边，容量为 \(\infty\)，费用为 \(c_i\times c_j\)。然后传统的建立超源和超汇，容量为 \(b_i\)，费用为 \(0\)​。

但是我们其实可以发现，这道题目并不是一个标准的最大费用最大流。它是在满足费用不小于 \(0\) 的情况下求最大流量。但是我们可以用最大费用最大流的思路，由于我们每次找的都是费用最大的，那么如果这一次的费用加上总费用之后小于 \(0\)，那么以后的费用都不可能让总费用变得大于等于 \(0\)。因此如果当前这条增广路对的费用加上去之后总费用仍然大于等于 \(0\)，那流量就可以加上这条路上的流量；否则就意味着这条增广路上的流量不能跑满，我们让他能跑多少跑多少，然后直接终止找增广路。

最后输出最大流量即可。

[SCOI2007] 修车

首先我们发现，对于一个技术人员 \(i\)，如果它要修 \(k\) 辆车，按顺序分别为 \(a_1,a_2,\cdots a_k\)，那么我们可以得出这个师傅的总用时为：

\[\begin{aligned} &\ T_{a_1,i}+(T_{a_1,i}+T_{a_2,i})+\cdots (T_{a_1,i}+T_{a_2,i}+\cdots+T_{a_k,i})\\ =&\ kT_{a_1,i}+(k-1)T_{a_2,i}+\cdots T_{a_k,i} \end{aligned} \]

我们发现这个式子似乎是可以连边的，但是实际上由于 \(k\) 并不知道，所以前面的系数是不确定的。

但是此时我们如果使用一下逆向思维，会发现对于倒数第 \(i\) 辆车，它前面的系数一定是 \(i\)。这样一来，我们就是用考虑每一辆车在每一个师傅中排倒数第几个即可，不需要知道 \(k\) 具体的值。

那么现在我们直接连边，首先将师傅拆成 \(n\) 个点，表示这个师傅倒数第 \(i\) 个车。对于每一辆车 \(p\)，向每一个师傅的每一个倒数的位置连边，对于第 \(i\) 个师傅的倒数第 \(j\) 辆车，费用为 \(T_{p, i}\times j\)。

那么费用限制其实就考虑完了，接下来看流量限制。首先从超源向每一辆车连容量为 \(1\)，费用为 \(0\) 的边。再从每一个师傅向超汇连容量为 \(1\)，费用为 \(0\) 的边。同时中间车向师傅连的边的容量也都为 \(1\)。

接下来我们跑最小费用最大流，求出的最小费用就是总的等待时间，然后除以 \(n\) 即可得到答案。

[NOI2012] 美食节

这道题是上一道题的加强版，因此建图思路是一致的。只列举不同的地方：

• 超源向每一道菜连的边的容量是 \(p_i\)。
• 每个师傅要拆成 \(p\) 个点。

这样我们直接提交，发现拿到了 \(60\) pts 的好成绩，剩下的全部 TLE。

考虑上面的思路不优在哪里，我们知道，对于一个师傅 \(i\) 以及倒数第 \(j\) 道菜，只有在它前面的 \(j-1\) 道全部放满了之后才会考虑这里。换句话说，我们将拆开的厨师看做二元组 \((i,j)\)，如果前面有 \((i,k)\) 没有选，那么肯定是选之前的那个更优。

也就是说，只有前面的菜都放满了，这个位置才有考虑的必要，在此之前都是没有必要的。既然这样我们是否可以考虑在之前不考虑这个点呢？

考虑动态加点的思想，每次 EK 都能找出一条增广路并增广，意味着这个位置可能会被占据；而当这个位置是当前这个厨师的最后一个位置时，我们就加上新的位置，然后对应连边。

在初始的时候我们都只给师傅的倒数第 \(1\) 个位置连上对应的边，之后在 EK 增广的过程中再慢慢加上剩余的边。这样，我们拆开的厨师的点数就始终是菜的数量，大大优化了时间复杂度。

[六省联考 2017] 寿司餐厅

首先这个题面长到爆炸，我们总结一下关键点：

• 一次必须取一段。
• 每一段下的所有子区间的 \(d\) 要累加。
• 重复的 \(d\) 只算一次。
• 收费为 \(mx^2+cx\)。

那么我们来关注第三四条，假如我们选了两个有重叠的区间，那么收的费用会多出一个 \(x\)，然而重复的 \(d\) 只算一次，就相当于亏了 \(x\)。又由于 \(x\) 肯定不是负数，所以贪心的想，我们肯定是尽量要让区间互不重叠。也就是说这个第三条不过是一个唬人的幌子罢了。

接下来考虑剩下的部分。由第二条可知，对于区间 \([l,r]\)，它的所有子区间都要选，那我们递归的想，只要让区间 \([l,r]\) 指向 \([l+1,r]\) 和 \([l,r-1]\)，那么一个区间下面的子树就是所有子区间。

接下来考虑收费，我们先看多吃一个 \(x\) 的贡献，显然就是 \(x\)。那根据上面递归的方式，我们只需要在叶子结点 \([i,i]\) 处将对应点权 \(d_{i,i}\) 减去 \(x\) 即可。然后考虑怎样算上 \(mx^2\)，由于这是一个定值，我们可以对所有的 \(x\) 新建一个节点，点权就是 \(-mx^2\)，让叶子结点指向对应的点即可。

我们总结一下上面的建图：

• 让 \([l,r]\) 指向 \([l+1,r]\) 和 \([l,r-1]\)，同时 \([l,r]\) 对应的点权为 \(d_{l,r}\)。
• 叶子结点 \([i,i]\) 的点权为 \(d_{i,i}-x_i\)。
• 对于每一个叶子结点 \([i,i]\)，让它指向点权为 \(-m{x_i}^2\) 的新建节点。

这样，我们在选的时候，必须要满足选了这个点就必须选它指向的点。而我们的目标是要让所有的点权加起来最大。不难发现现在的条件完全就是一个最大权闭合子图的模板，直接套上去即可。

[SDOI2010] 星际竞速

这道题有两种思路，一种很好想，另一种不太好想。

先说好想的思路。

首先我们看到题目中有关于必须走一次这样的限制，不难想到上下界网络流。对于每一个点 \(x\) 拆成两个点 \(x_1,x_2\)，连 \(x_1\to x_2\)，上下界均为 \(1\)，费用为 \(0\)。

考虑连剩下的边。根据题意，我们需要将所有通道的边连上，同时每一个点还可以通过爆发到达任意一个其他点，因此还要将这些边连上。此时我们容易发现，边数已经来到了 \(n^2\)，而且还甚至是下界。所以此时使用朴素 SPFA+EK 复杂度上界就是 \(O(V^2E^2)=O(n^2n^4)=O(n^6)\)。就算这上界很松这都是不可能过掉的。考虑优化。

我们会发现这样一件事，如果我们在比赛途中使用爆发，由于爆发到 \(i\) 的花费都是固定的 \(A_i\)，因此无论从哪个点爆发其实和从起点爆发的效果都是一样的。所以我们可以将爆发看作是退回到起点然后再走一条路径。这样我们其实就不需要再连中间所有点爆发的结果，只需要从源点向每个入点连上下界为 \([0,+\infty)\)，费用为 \(A_i\) 的边即可。

这样做边的数量就差不多是 \(m\) 了，时间复杂度上界为 \(O(n^2m^2)\)，上界比刚才那个宽松了大约 \(2000\) 倍。

最后我们直接跑一个有源汇上下界最小费用可行流即可。

Tips：容易发现，经过这一步简单的转化，本质上这道题与 [bzoj2055] 80人环游世界 没有任何差别。

接下来是不太好想的思路，我们可以不需要上下界，直接使用最小费用最大流。

首先还是得先拆点，让 \(x_2\) 流向汇点，流量 \(1\) 费用 \(0\)。然后我们考虑 \(x_2\) 都可以怎么来，显然有两种方式：走星际航路或能力爆发。对于前者，我们将一条星际航路 \((u,v)\) 连 \(u_1\to v_2\) 的边。对于后者，直接从源点像 \(x_2\) 连流量 \(1\) 费用 \(a_x\) 的边即可。

最后考虑 \(x_1\) 的流量从何而来，显然从源点连流量 \(1\) 费用 \(0\) 的边即可。最后跑最小费用最大流。

这种操作就不是很寻常，当然其中有一些思想是第一种方法也用到的。

[清华集训 2017] 无限之环

有一点码农题的味道。

首先我们发现这道题根本看不出来是一道网络流。考虑数据范围，只有 \(15\) 个管子可以想到状压，但是似乎不是很可做。接着看到水管和网格，结合起来就可以十分牵强自然的想到网络流。

首先不考虑旋转，先看怎样连边。容易发现这个网格中行列没有限制而每个格子有限制，自然想到黑白染色，从白格向黑格连边。接下来继续考虑接口的限制，自然没有旋转的时候可以直接连边，但是有旋转显然不行。

考虑到旋转之后状态会改变，于是可以想到将一个点拆成能够旋转成的所有状态，然后连上对应次数作为费用。听上去很可行但实则不然，因为这样我们的流量表示的就是这个水管流出的接口数，这样与我们要求的操作次数八竿子打不着，因此这样是错误的。

那么我们这样考虑：将一个点拆成上中下左右五个点，其中这中间的点来代表这个点，与源汇点相连。剩下四个点，表示这个方格周围的四个接口。那么我们此时从白格向黑格连边，就可以直接将对应方位的接口连起来即可。

接下来我们以白格（连源点的格子）为例考虑。首先初始的时候这个格子有哪些接口相同，就将中间的点向对应的接口相连，流量 \(1\) 费用 \(0\)。然后就是这个题最最关键的地方：旋转操作。

首先看最简单的，只有一个接口的那个水管。

假如我们本来是向上的，那么应该是中点向上点连边。这代表向上的接口有 \(1\) 的流量。此时我们向右旋转，就代表原先向上接口 \(1\) 的流量转移到了向右接口，同时花费 \(1\)​ 的费用。

思考一下上面的那一段话，然后我们会连出这样一条边：从上点向右点连边，流量 \(1\) 费用 \(1\)。这样我们如果向旋转到右边，刚好可以满足上面那段话说的所有条件。剩下的边同理。

于是我们就得到了这道题旋转的真正思路：用原来的边表示流量，新加的边来表示旋转后流量的转移。

根据这个理论，我们就可以轻松搞出剩下格子中的边。

接下来考虑 L 型水管。

假如水管是正 L，那么初始的时候应该是中点向上点和右点连边。如果顺时针旋转一次，那么相当于上点的流量转移到了下点，于是从上点向下点连边。同理从右点向左点连边。

此时会发现我们似乎并没有考虑转两次的情况，但仔细思考就会发现，如果上点右点的流量都转移，那么费用是 \(2\)，刚好对应旋转两次后的情况。所以这样连边是完全正确的。

最后看 T 型水管。

此时初始的时候应该是中点向左点下点和右点连边。那么旋转一次后左点或右点的流量会转移到上点，而旋转两次后下点的流量会转移到上点。那么我们直接连边即可。

最最后 X 型水管根本不用管，直接连好所有边即可。I 型水管也不用管，因为题目不让管。

那么对于黑格，只需要将上面的边全部反过来，朝向汇点方向即可。

最后我们从源点出发，跑一遍最小费用最大流。如果最大流流量 \(\times\ 2\) 正好是所有水管接口数之和则代表有解，直接输出最小费用就是答案。

其实不能动直线型水管的原因很简单了：在这样的建图方式下，转一次直线型水管意味着两个接口的流量都要转移，而网络流是没有办法实现让它必须同时转移的，因此不动直线型水管其实是标答的漏洞吧。

[NOI2010] 海拔

首先我们观察题目，不难注意到以下几点：

• 点的高度是任意的实数，且需要互不相同。
• 起点高度为 \(0\)，终点高度为 \(1\)。

这样来看这道题似乎不简单，尤其这些条件看上去很唬人。但是我们显然可以简化他们。下面通过三个引理来说明。

引理 \(1\)：最优情况一定是所有高度在取到 \([0,1]\) 时。

证明：显然可得，如果一个点高度 \(<0\) 或 \(>1\)，那么将他改为 \(0\) 或 \(1\) ，对于从他出发的边不会更差，而到达他的边走的高度会更优。

引理 \(2\)：一定会有一种最优方案在所有高度取到 \(0\) 或 \(1\) 的时候。

证明：考虑任意一条从 \(s\) 到 \(t\) 的路径，显然高度都必须上升 \(1\)。那根据上面引理 \(1\) 的结论，显然所有点要取在 \([0,1]\) 之间，于是我们得到只有在这条路上所有点高度严格不降时才会更优。那么我们设高度升高的边的边权分别为 \(w_1,w_2,\cdots,w_k\)，高度分别上升 \(h_1,h_2,\cdots,h_k(h_1+h_2+\cdots h_k=1)\)。此时代价显然是 \(w_1h_1+w_2h_2+\cdots+w_kh_k\)。考虑 \(w\) 中最小的一个 \(w_p\)，如果我们只让 \(h_p=1\)，那么此时的代价就是 \(w_p\)。那么我们一定会有：

\[\begin{aligned} w_p&=w_p\times 1\\ &=w_p\times(h_1+h_2+\cdots h_k)\\ &=w_ph_1+w_ph_2+\cdots+w_p+h_k\\ &\le w_1h_1+w_2h_2+\cdots+w_kh_k \end{aligned} \]

于是就可以得到，对于一条路径，只要选取边权最小的一条边 \(u,v\)，让 \(h_u=0,h_v=1\) 即可达到最小。剩余的分别取 \(0\) 或 \(1\) 即可。照此推广到全局同样如此，不断按照最优策略换成 \(0\) 或 \(1\)，答案一定不会更差，也就是一定会有一组最优方案满足所有点高度都为 \(0\) 或 \(1\)​。

当然我们会细心的发现题目中要求高度互不一致，而此时我们却说所有点高度都是 \(0,1\)，似乎有失偏颇。其实这个问题同样简单，发现题目的输出只需要保留到整数，所以我们给每一个点权减去或加上互不相同的极小的一个量 \(\Delta_i\)，这样就能满足互不相同的条件，而答案是不变的。

引理 \(3\)：在 引理 \(2\) 的基础上，该最优方案一定满足高度为 \(0\) 的点与高度为 \(1\) 的点构成联通块，且分别包含 \(s,t\)。

证明：以高度为 \(0\) 的点举例。假如 \(s\) 周围高度为 \(0\) 的联通块中有高度为 \(1\) 的联通块，那么将这些高度为 \(1\) 的点都变成 \(0\) 显然会更优。高度为 \(1\) 同理。所以高度 \(0\) 的点和高度 \(1\) 的点一定都联通。

根据引理 \(2\) 我们知道，所有点取 \(0,1\) 会最优。根据引理 \(3\) 我们也知道高度为 \(0\) 的点与高度为 \(1\) 的点一定构成联通块。那么此时我们再看走的代价就很明确了，也就是所有从高度为 \(0\) 的联通块走向高度为 \(1\) 的联通块的边权之和。那么高度为 \(0\) 的联通块就是 \(s\) 的联通块，高度为 \(1\) 的联通块就是 \(t\) 的联通块。那么也就是说，我们要求出从 \(s\) 联通块到 \(t\) 联通块的所有边边权最小的和。

这不就十分显然了吗，直接跑最小割即可。但是我们发现会 T 一个点。

考虑到这个网格图一定是平面图，这就想到了平面图最小割转对偶图最短路。按照传统功夫做出对偶图的 \(S,T\)，将原图中每一条边顺时针旋转 \(90\degree\) 连边即可。

[NOI2008] 志愿者招募

据我所知这道题至少有三种解法。下面按照思考难度从易到难讲解。

Solution 1：

考虑到题目中有 “至少需要 \(a_i\) 个人” 的限制，按照传统功夫自然想到上下界网络流。那么对于每一天拆成两个点 \(i_x,i_y\)。首先要连 \((i_x,i_y,[a_i,\infty],0)\)。

接下来我们考虑对于每一类志愿者建立一个点 \(p_i\)，那么我们先连 \((p_i,l_i,[0,\infty],c_i)\)。然后考虑志愿者服务区间的问题，我们想到可以对志愿者进行传递。那么自然连 \((i_y,i_x,[0,\infty],0)\)。但是这样我们只是考虑到了志愿者的起始天和中间的传递，没有考虑到它们的终止天。假如对于第 \(i\) 类志愿者派出了 \(r_i\) 个人，那么在终止天的时候就应该将这 \(r_i\) 个人收回。于是再连 \((r_i,p_i,[0,\infty],0)\)。这样只要 \(p_i\) 流量守恒，那么派出去的志愿者就一定会收回。我们其实并不在乎这些志愿者是什么种类，只要数量够了就行。

此时我们显然是要求最小费用，那么直接跑无源汇上下界最小费用可行流即可。同时容易发现其实 \(p_i\) 这个点根本无用，因此直接连 \((r_i,l_i,[0,\infty],c_i)\)​ 即可。

其实做了这么多题不难发现，上下界网络流的思路往往最为直观好想，当然代价就是跑的比较慢。

Solution 2：

容易发现，题目的所有要求可以概括为：

设 \(x_i\) 是第 \(i\) 类志愿者的数量，求出 \(\sum\limits_{i=1}^n x_i c_i\) 最小值，同时对于 \(i\in [1,n]\) 还要满足 \(\sum\limits_{l_j\le i\le r_j}x_j\ge a_i\)。

不难发现，上面这个问题就是一个显然的线性规划问题。那我们就可以直接按套路走。首先将不等式化为等式：

\[\sum\limits_{l_j\le i\le r_j}x_j-y_i= a_i \]

现在对相邻式子做差得：

\[\sum\limits_{l_j\le i\le r_j}x_j-\sum\limits_{l_j\le i-1\le r_j}x_j-y_i+y_{i-1}= a_i-a_{i-1} \]

此时我们不难发现，当 \(l_j=i\) 的时候，\(x_j\) 只会在第一个和式中出现，于是在剩下的项抵消之后会留下 \(x_j\)；当 \(r_j=i-1\) 的时候，\(x_j\) 只会在第二个和式中出现，于是在剩下的项抵消之后会留下 \(-x_j\)。同时 \(y_i\) 在第 \(i\) 个等式中为负，第 \(i+1\) 个等式中为正。这样我们就满足了每个变量出现两次且一正一负的要求。

那么接下来我们就可以直接开始建图，直接套用模板即可：

• 建立 \(n+1\) 个点代表等式，以及源点 \(S\) 汇点 \(T\)。
• 对于 \(i\in [1,n]\)，若 \(a_i-a_{i-1} \ge 0\)，连边 \((S,i,a_i-a_{i-1},0)\)；否则连 \((i,T,a_{i-1}-a_i,0)\)。
• 对于所有变量 \(x_i\)，显然在第 \(l_i\) 个等式中为正，第 \(r_i+1\) 个等式中为负。那么连 \((l_i,r_i+1,\infty,c_i)\)。
• 对于所有变量 \(y_i\)，显然在第 \(i+1\) 个等式中为正，第 \(i\) 个等式中为负。那么连 \((i+1,i,\infty,0)\)。

最后跑最小费用最大流即可。

Solution 3：

我们直接从题目的实际含义下手。

首先我们考虑对于每一天建立一个点。然后同时还要源点 \(S\) 汇点 \(T\)。

先考虑表示出每个志愿者管辖的区间范围。我们希望让他转化为覆盖边，因为这样我们才能转化为流量上单的问题，所以我们考虑连边 \((l_i,r_i+1,\infty,c_i)\)。

然后接下来考虑人数限制。我们不妨从简单情况入手，考虑只有一个志愿者，区间为 \([l,r]\)，我们就会连上 \((l,r+1,\infty,c)\) 的边。然后是每一天的人数限制，显然如果此时只有一个志愿者，那么刚才那条边上流过的流量就应该等于所有 \(a_i\) 的最大值。那么我们就可以直接连 \((i,i+1,-a_i,0)\)。 如果从 \(l\) 到 \(r+1\) 之间的边跑满，总流量就相当于所有 \(a_i\) 的最大值的相反数。如果此时我们让 \(r+1\) 这一个点通过的流量是 \(0\)，就代表着最开始我们连的那一条 \((l,r+1)\) 的边的流量，即志愿者人数，为 \(a_i\) 的最大值。

这样我们通过流量守恒就可以让志愿者与人数限制匹配，当然网络流流量不能是负的，我们可以给他们全部加上 \(\infty\)，这样到最后的汇点的流量之和就应该是 \(\infty\)。为了满足流量守恒，源点流出的流量自然也就是 \(\infty\)。

最后总结建图如下：

• 建立源点 \(S=0\)，汇点 \(T=n+2\)。连边 \((S,1,\infty,0),(n+1,T,\infty,0)\)。
• 连边 \((l_i,r_i+1,\infty,c_i)\)。
• 连边 \((i,i+1,\infty-a_i,0)\)。

这样我们直接求出最小费用最大流即可。

最后尝试发现，三种解法所用时间也是依次递减的。

[SDOI2017] 新生舞会

其实这道题的难点就在于我不会 01 分数规划，会了这个东西之后这道题就异常简单了。

首先我们会想到 dp，但是显然的问题是这个 dp 是有后效性的，也就是说会存在 \(\dfrac{a_1}{b_1}<\dfrac{a_2}{b_2}\)，但是却有 \(\dfrac{a_1+c}{b_1+d}>\dfrac{a_2+c}{b_2+d}\) 的情况（容易构造，移项展开后随便填数就行）。于是 dp 自然作废。

接下来就不难发现题目的 \(C\) 其实就是一个 \(\dfrac{\sum w_ia_i}{\sum w_ib_i}(w_i=0,1)\) 的模式，自然想到 01 分数规划。利用二分，设当前二分的最大值为 \(c\)，那么就是要满足 \(\dfrac{\sum w_ia_i}{\sum w_ib_i}\ge c\) 才能转移二分区间并记录答案。移项合并后得 \(\sum w_i(a_i-cb_i)\ge 0\)。现在就是要让左边最大，然后看是否大于 \(0\) 即可。于是问题就转化为求 \(\sum w_i(a_i-cb_i)\) 的最大值。

这个时候我们会发现，将男生看作一部点，女生看作另一部点，就构成了一个二分图。如果我们此时将男生 \(i\) 向女生 \(j\) 连边，费用为 \(a_{i,j}-cb_{i,j}\)，那么我们直接进行二分图最大匹配就可以直接求出答案。那我们使用传统网络流也很简单，建图如下：

• 建立源点 \(S\)，设 \(i\) 为男生，连边 \((S,i,1,0)\)。
• 建立汇点 \(T\)，设 \(j\) 为女生，连边 \((i,T,1,0)\)。
• 设 \(i\) 为男生， \(j\) 为女生，连边 \((i,j,1,a_{i,j}-cb_{i,j})\)。

跑出最大费用最大流，最大费用就是 \(\sum w_i(a_i-cb_i)\) 的最大值。

最后直接输出二分的答案即可。