点分治

1 点分治概念

点分治是树分治的一种，主要用于处理树上路径问题。

注意这颗树不需要有根，即这是一颗无根树。

下面以例题分析点分治的基本思想。

2 点分治实现

2.1 思想

首先你需要会的前置知识：树的重心。

我们来看这样一道例题：【模板】点分治：

给出一颗无根树，有边权，询问树上是否存在距离为 \(k\) 的点。

首先会有显然的树上差分做法，不过太劣。

考虑这样一件事：对于树上的所有路径，可以分成两部分：

经过当前根节点的。
不经过当前根节点的。

对于第二种情况，他们一定在根节点的某个子树中。

我们发现，只要我们求出第一种情况对应的方案数，那么第二种情况就可以递归求解。

于是我们现在就有了点分治的初步思路：将路径分为经过与不经过根节点，对于后者继续递归分开求解。

但是如果直接随机取根节点求解，说不定会被卡成 \(O(n)\)（一条链）。此时就要提到上面强调的一个东西：由于原树是无根树，所有选择根节点的权利在于我们手里。我们只需要让他深度平衡，就可以保证复杂度为 \(O(\log n)\)。

那么如何让根节点平衡呢？这就要用到前置知识了：对于每一颗子树，让他的重心成为当前根节点就可以保证平衡。

所以我们总结一下点分治的基本步骤：

找出当前子树的重心。
根据题意对于当前子树的答案进行统计。
分治各个子树，重复步骤 \(1\)。

这就是点分治的基本思想了。

接下来就是代码了。

2.2 代码

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;
const int Maxn = 2e5 + 5;
const int Maxm = 1e7 + 5;

int n, m;
int head[Maxn], edgenum;
struct node {
	int nxt, to, w;
}edge[Maxn];

void add(int from, int to, int w) {
	edge[++edgenum] = {head[from], to, w};
	head[from] = edgenum;
}

int q[Maxn];
bool ok[Maxm];

struct pdac {
	bool del[Maxn];
	int siz[Maxn], cen, sum;
	void getcen(int x, int fa) {//求重心
		siz[x] = 1;
		int s = 0;
		for(int i = head[x]; i; i = edge[i].nxt) {
			int to = edge[i].to;
			if(del[to] || to == fa) continue;
			getcen(to, x);
			siz[x] += siz[to];
			s = max(s, siz[to]);
		}
		s = max(s, sum - siz[x]);
		if(s <= sum / 2) cen = x;
	}
	int dis[Maxn], cnt, d[Maxn];
	void getdis(int x, int fa) {//求当前子树各个节点到根节点的距离
		dis[++cnt] = d[x];
		for(int i = head[x]; i; i = edge[i].nxt) {
			int to = edge[i].to;
			if(del[to] || to == fa) continue;
			d[to] = d[x] + edge[i].w;
			getdis(to, x);
		}
	}
	bool vis[Maxm];
	int p[Maxn], tot;
	void dfs(int x) {//点分治
		del[x] = 1;
		vis[0] = 1;
		tot = 0;
		for(int i = head[x]; i; i = edge[i].nxt) {
			int to = edge[i].to;
			if(del[to]) continue;
			cnt = 0, d[to] = edge[i].w;
			getdis(to, x);
			for(int j = 1; j <= cnt; j++) {
				for(int k = 1; k <= m; k++) {
					if(q[k] >= dis[j]) {
						ok[k] |= vis[q[k] - dis[j]];//能否拆分 q[k]
					}
				}
			}
			for(int j = 1; j <= cnt; j++) {
				if(dis[j] >= Maxm) continue;//注意距离可能大于 k 的最大值，此时我们不需要存储，否则会 RE
				p[++tot] = dis[j];
				vis[dis[j]] = 1;
			}
		}
		for(int i = 1; i <= tot; i++) {//不要用 memset，会 TLE
			vis[p[i]] = 0;
		}
        //上：处理当前点信息
        //下：分治求解
		for(int i = head[x]; i; i = edge[i].nxt) {
			int to = edge[i].to;
			if(del[to]) continue;
			sum = siz[to];
			getcen(to, 0);
			getcen(cen, 0);//跑两边，求出以重心为根各个子树的大小
			dfs(cen);
		}
	}
	void solve() {
		sum = n;
		getcen(1, 0);
		getcen(cen, 0);//同理，跑两边
		dfs(cen);
		for(int i = 1; i <= m; i++) {
			if(ok[i]) {
				cout << "AYE\n";
			}
			else {
				cout << "NAY\n";
			}
		}
	}
}T;

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0), cout.tie(0);
	cin >> n >> m;
	for(int i = 1; i < n; i++) {
		int u, v, w;
		cin >> u >> v >> w;
		add(u, v, w), add(v, u, w);
	}
	for(int i = 1; i <= m; i++) {
		cin >> q[i];
	}
	T.solve();
	return 0;
}

3 动态点分治

动态点分治，它是基于点分治然后加以变化，构建出一颗重构树，就叫做点分树。

下面讲解点分树的基本概念及例题。

3.1 基本概念

我们知道，对于单次查询树上路径相关的问题可以采用点分治解决。

但是如果加上一些修改和多次查询，点分治显然无法胜任。

考虑我们一般见到树上操作的处理方式，无外乎转化然后利用数据结构维护。那么我们得先将原树转化一下。

考虑按点分治的思想建树。我们将当前子树的重心作为根节点，与上一个根节点（也就是上一层树的重心）连边，这样我们就得到了一颗重构树，这就是点分树。

例如下图所示：

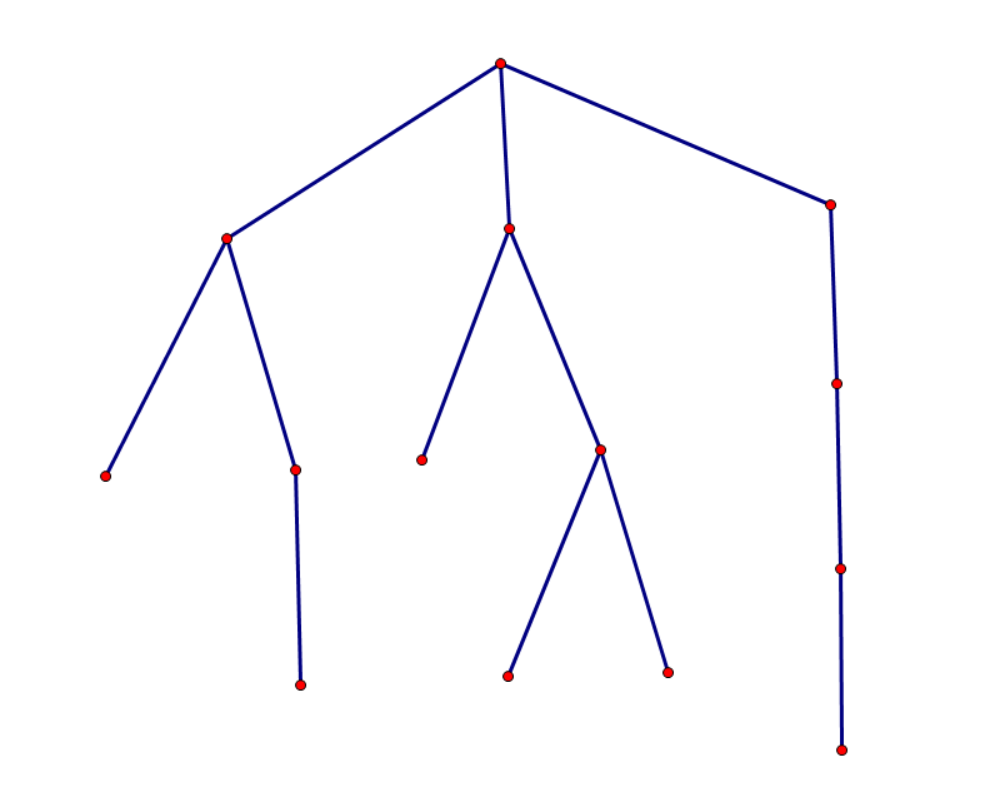
构造点分树为：

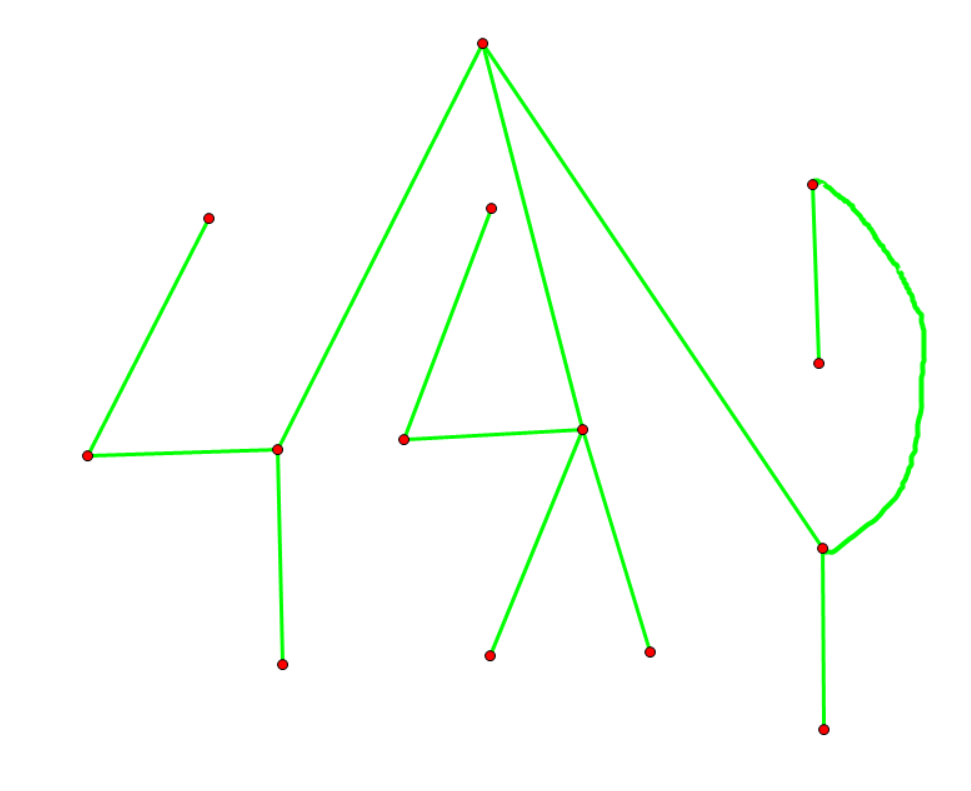
我们会发现，新的重构树与原树基本上没有什么共同之处，几乎所有父子关系都被破坏。

但是我们会注意到一点：由于每一次选的都是重心，因此树高不会超过 \(\log n\)，这样的性质可以帮助我们优化一部分时间复杂度。

同时我们还会得到这样一条性质：对于两点 \(x,y\)，他们在点分树上的 LCA 点 \(l\) 一定在原树 \(x\to y\) 的路径上。

感性证明如下：

当我们找到 \(lca(x,y)\) 时，这个点所对应的子树也对应着原树上的一个子树。

同时由于我们找到的是 LCA，那么我们在以这个点为根划分子树的时候，一定会将 \(x,y\) 分开，那么 \(x\to y\) 的路径上就自然包含 LCA。

得到这些性质有什么用呢？我们接下来看一道例题。

3.2 例题

【模板】点分树 | 震波

有一棵树，每个点有权值 \(a_i\)，每次进行两种操作中一种：

给出 \(x,y\)，将 \(a_x\) 改为 \(y\)。

给出 \(x,k\)，求出 \(\sum\limits_{dis(x,y)\le k} a_y\)。

我们考虑利用点分树。

我们的重点在于操作 \(2\)。此时 \(x\) 是固定的，而 \(y\) 在变化。我们枚举 \(x,y\) 在点分树上所有可能的 LCA，记为 \(l\)。那么根据上面的性质可以得到 \(dis(x,y)=dis(x,l)+dis(l,y)\)（注意这里的 \(dis\) 是原树上的）。

由于我们上面已经求得树的深度为 \(\log n\)，因此枚举 LCA 也是 \(O(\log n)\) 的。

那么我们要求的答案就可以转化为：

\[\sum\limits_{dis(x,l)+dis(l,y)\le k\cap lca(x,y)=l} a_y \]

移项得：

\[\sum\limits_{dis(l,y)\le k-dis(x,l)\cap lca(x,y)=l} a_y \]

我们此时在固定 \(l\) 的前提下，已经将下面的式子转化为了 \(y\) 的式子。

首先考虑怎样的 \(y\) 满足 \(lca(x,y)=l\)。显然所有的点集就是 \(l\) 的子树去掉 \(l\) 在 \(x\) 方向上的儿子 \(p\) 的子树。

那么我们现在要求的是这些点中满足 \(dis(l,y)\le k-dis(x,l)\) 的权值和。我们按照上面刨除子树的思路，答案就是 \(l\) 的子树内到 \(l\) 的距离 \(\le k-dis(x,l)\) 的点权值和减去 \(p\) 的子树内到 \(l\) 的距离 \(\le k-dis(x,l)\) 的点权值和。

考虑如何维护这个东西。我们现在要支持对于每一个点维护子树点权值和、单点修改、查询前缀和。显然对于每一个点建立一颗动态开点线段树即可，具体的，对于点 \(x\)，下标为 \(i\) 表示 \(x\) 子树内满足 \(dis(x,p)=i\) 的 \(a_p\) 之和。

那么我们就可以求出 \(l\) 的子树内到 \(l\) 的距离 \(\le k-dis(x,l)\) 的点权值和。

问题在于 \(p\) 的子树内到 \(l\) 的距离 \(\le k-dis(x,l)\) 的点权值和我们仍不好求。我们此时考虑再建立一颗动态开点线段树，具体的，对于点 \(x\)，下标为 \(i\) 表示 \(x\) 子树内满足 \(dis(fa_x,p)=i\) 的 \(a_p\) 之和（注意这里的 \(fa_x\) 是在原树上的）。这样我们简单维护即可。

剩下的就是代码了。

3.3 代码

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;
const int Maxn = 2e5 + 5;
const int Maxm = 4e6 + 5;

int n, q;
int w[Maxn];

int head[Maxn], edgenum;

struct node {
	int nxt, to;
}edge[Maxn];

void add(int from, int to) {
	edge[++edgenum] = {head[from], to};
	head[from] = edgenum;
}

struct Tree {//预处理原树信息，包括 dis 和 fa
	int dep[Maxn], siz[Maxn], fa[Maxn], son[Maxn], top[Maxn], ind;
	void dfs1(int x) {
		siz[x] = 1;
		son[x] = -1;
		for(int i = head[x]; i; i = edge[i].nxt) {
			int to = edge[i].to;
			if(to == fa[x]) continue;
			dep[to] = dep[x] + 1;
			fa[to] = x;
			dfs1(to);
			siz[x] += siz[to];
			if(son[x] == -1 || siz[to] > siz[son[x]]) {
				son[x] = to;
			}
		}
	}
	void dfs2(int x, int rt) {
		top[x] = rt;
		if(son[x] == -1) return ;
		dfs2(son[x], rt);
		for(int i = head[x]; i; i = edge[i].nxt) {
			int to = edge[i].to;
			if(to == fa[x] || to == son[x]) continue;
			dfs2(to, to);
		}
	}
	int lca(int x, int y) {
		while(top[x] != top[y]) {
			if(dep[top[x]] < dep[top[y]]) {
				swap(x, y);
			}
			x = fa[top[x]];
		}
		return dep[x] < dep[y] ? x : y;
	}
	int dis(int x, int y) {
		return dep[x] + dep[y] - 2 * dep[lca(x, y)];
	}
}T;

#define lp t[p].l
#define rp t[p].r

struct SegTree {//动态开点线段树
	int rt[Maxn];
	struct node {
		int l, r, sum;
	}t[Maxm];
	int cnt = 0;
	void pushup(int p) {
		t[p].sum = t[lp].sum + t[rp].sum;
	}
	void mdf(int &p, int l, int r, int x, int val) {
		if(!p) p = ++cnt;
		if(l == r) {
			t[p].sum += val;
			return ;
		}
		int mid = (l + r) >> 1;
		if(x <= mid) mdf(lp, l, mid, x, val);
		else mdf(rp, mid + 1, r, x, val);
		pushup(p);
	}
	int query(int p, int l, int r, int ql, int qr) {
		if(!p) return 0;
		if(ql <= l && r <= qr) {
			return t[p].sum;
		}
		int mid = (l + r) >> 1;
		if(qr <= mid) return query(lp, l, mid, ql, qr);
		else if(ql > mid) return query(rp, mid + 1, r, ql, qr);
		else return query(lp, l, mid, ql, mid) + query(rp, mid + 1, r, mid + 1, qr);
	} 
}seg1, seg2;

struct PointTree {
	bool vis[Maxn];
	int siz[Maxn], cen, sum;
	void getcen(int x, int fa) {//找到重心
		siz[x] = 1;
		int s = 0;
		for(int i = head[x]; i; i = edge[i].nxt) {
			int to = edge[i].to;
			if(to == fa || vis[to]) continue;
			getcen(to, x);
			siz[x] += siz[to];
			s = max(s, siz[to]);
		}
		s = max(s, sum - siz[x]);
		if(s <= sum / 2) cen = x;
	}
	int fa[Maxn];
	void dfs(int x) {//记录每个点在点分树上的父亲即可
		vis[x] = 1;
		for(int i = head[x]; i; i = edge[i].nxt) {
			int to = edge[i].to;
			if(vis[to]) continue;
			sum = siz[to];
			getcen(to, 0);
			getcen(cen, 0);
			fa[cen] = x;
			dfs(cen);
		}
	}
	void mdf(int x, int val) {//修改权值
		int p = x;//p 是枚举的 lca
		while(p) {//需要修改所有可能 lca 的线段树
			seg1.mdf(seg1.rt[p], 0, n - 1, T.dis(x, p), val);//修改
			if(fa[p]) {
				seg2.mdf(seg2.rt[p], 0, n - 1, T.dis(x, fa[p]), val);
			}
			p = fa[p];
		}
	}
	int query(int x, int k) {
		int p = x, pre = 0, ans = 0;//p 是枚举的 lca, pre 是 p 在 x 方向上的子树
		while(p) {
			if(T.dis(x, p) > k) {//避免出现负数下标导致 RE
				pre = p, p = fa[p];
				continue;
			}
			ans += seg1.query(seg1.rt[p], 0, n - 1, 0, k - T.dis(x, p));//查询
			if(pre) {
				ans -= seg2.query(seg2.rt[pre], 0, n - 1, 0, k - T.dis(x, p));//刨除这一部分子树
			}
			pre = p, p = fa[p];
		}
		return ans;
	}
	void solve() {
		T.dfs1(1);
		T.dfs2(1, 1);//预处理
		sum = n;
		getcen(1, 0);
		getcen(cen, 0);
		dfs(cen);//构造点分树
		for(int i = 1; i <= n; i++) {
			mdf(i, w[i]);//用单点修改建树
		}
		int pre = 0;
		while(q--) {
			int opt, x, y;
			cin >> opt >> x >> y;
			x ^= pre, y ^= pre;
			if(opt == 0) {
				pre = query(x, y);
				cout << pre << '\n';
			}
			else {
				mdf(x, y - w[x]);//修改偏移量
				w[x] = y;
			}
		}
	}
}PT;

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0), cout.tie(0);
	cin >> n >> q;
	for(int i = 1; i <= n; i++) {
		cin >> w[i];
	}
	for(int i = 1; i < n; i++) {
		int u, v;
		cin >> u >> v;
		add(u, v), add(v, u);
	}
	PT.solve();
	return 0;
}

posted @ 2024-04-21 10:05 dingzibo_qwq 阅读(5) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

dzbblog

点分治