机器学习之线性回归模型

公告

View Post

如果你在上面找线的过程所找的线直的，那么这个找直线的过程就是“线性回归”，线性回归可分为：简单一元线性回归和多元线性回归，也就是我们平时接触的一次线性方程和多次线性方程，二者的主要区别也就是未知项的个数。

一、简单一元线性回归

一元线性方程的公式：y=wx+b
给你两个点，你就能确定其中的参数w和b，之后我们就能在直角坐标系中画出相应的一条直线来，有了这条线，随便扔给你一个x，你都能够通过这个函数式子求出y的值，通过求函数中的参数来找直线的过程就是线性回归。
当只用一个x来预测y，就是简单一元线性回归，也就是在找一个直线来拟合数据。

二、多元线性回归

预测一个地方的房价，评估你的薪资，或者衡量某个人是否符合你找对象的标准等等这些，我们可定会从多个维度考察并综合衡量这些因素，所以怎么使得预测更加准确呢？那就多加入一些预测信息，机器学习中也把这些预测信息叫作特征，特征多了，我们的预测也就会靠谱的多，同时，特征增多了，原来的参数也就不够用了。有几个特征就会有几个参数，即让每一个特征对应一个参数，这用多个x来预测y，就是多元线性回归，也可以引出线性回归的一般表达式：

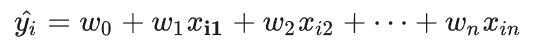
三、为什么使用线性回归

回归分析统计估计了两个或者多个变量之间的关系，由一个简单的例子进行下一步的加深理解：比如，在当前的经济条件下，你要估计一家公司的销售额增长情况，现在你有公司最新的数据，这些数据显示出销售额增大大约是经济增长的2.5倍。那么使用回归分析，我们就可以根据当前和过去的信息来预测未来公司的销售情况
根据上述例子我们可以得到以下信息：、
1、我们可以将销售额的增长率定义为：销售额增长率=公司销售额增长/经济增长
2、销售额增长大约是经济增长的2.5倍，因此，我们可以将上述式子转化为：销售额增长率=2.5
现在我们可以使用历史数据来拟合这个模型，然后使用该模型来预测未来的销售额情况，如果我们发现公司的销售额增长率偏离了预测值，我们可以重新调整模型并进行更新，回归分析是一种统计学方法，它基于历史数据与一些假设来进行预测。因此，在使用回归分析进行预测时，我们需要谨慎地考虑这些假设，以及历史数据是否足够可靠和全面。

四、线性回归的实验步骤

1、数据预处理
（1）数据收集：首先，你需要收集与问题相关的数据集，这些数据集应该包含自变量（特征）和因变量（目标）。
（2）数据清洗：清洗数据可以去除噪声、缺失值、异常值等。对于缺失值，你可以选择删除、填充或插值等方法进行处理。
（3）特征工程：根据需要，对数据进行特征转换或创建新的特征。这有助于模型更好地捕捉数据中的模式。
（4）数据划分：将数据集分为训练集、验证集和测试集。通常，我们使用的训练集来训练模型，验证集来调整超参数，测试集来评估模型的性能。
2、模型训练
（1）定义模型：指定线性回归模型的形式，即y=wx+b，其中w是权重，b是偏置项。
（2）初始化参数：为权重w和偏置项b分配初始值。这些初始值通常是随机选择的。
（3）定义损失函数：选择均方误差（MSE）作为损失函数，用于衡量模型预测值与实际值之间的差异。
（4）选择优化算法：选择一种优化算法（如梯度下降、随机梯度下降、Adam等）来预测最小化损失函数。这些算法通过迭代更新权重和偏置项的值来找到最优解。
（5）迭代训练：在训练集上迭代训练模型。在每次迭代中，使用优化算法跟新权重和偏置项的值，并计算损失函数。重复此过程直到满足停止条件（如达到预设1的迭代次数、损失函数低于某个阈值等）
3、模型评估
（1）计算损失函数：在验证集或测试集上计算模型的损失函数值，以评估模型的性能。
（2）计算其他指标：根据需要，计算其他评估指标，如R方值、均方根误差（RMSE）等。这些指标可以提供关于模型性能的更多信息。
4、模型应用
（1）预测新数据：使用训练好的模型对新的数据进行预测。这可以通过将新数据的特征输入到模型中并获取输出值来实现。
（2）解释结果：根据模型的预测结果，解释自变量对因变量的影响。则可以通过查看权重和偏置项的值来实现。

五、使用Python实现线性回归

1、导入必要的库

点击查看代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

2、生成模拟数据

点击查看代码

# 生成一些随机数据
np.random.seed(0)
x = 2 * np.random.rand(100, 1)
y = 4 + 3 * x + np.random.randn(100, 1)

# 可视化数据
plt.scatter(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Generated Data From Runoob')
plt.show()

3、使用Scikit-learn进行线性回归

点击查看代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

# 生成一些随机数据
np.random.seed(0)
x = 2 * np.random.rand(100, 1)
y = 4 + 3 * x + np.random.randn(100, 1)

# 创建线性回归模型
model = LinearRegression()

# 拟合模型
model.fit(x, y)

# 输出模型的参数
print(f"斜率 (w): {model.coef_[0][0]}")
print(f"截距 (b): {model.intercept_[0]}")

# 预测
y_pred = model.predict(x)

# 可视化拟合结果
plt.scatter(x, y)
plt.plot(x, y_pred, color='red')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Linear Regression Fit')
plt.show()

4、手动实现梯度下降法

点击查看代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

# 生成一些随机数据
np.random.seed(0)
x = 2 * np.random.rand(100, 1)
y = 4 + 3 * x + np.random.randn(100, 1)

# 初始化参数
w = 0
b = 0
learning_rate = 0.1
n_iterations = 1000

# 梯度下降
for i in range(n_iterations):
    y_pred = w * x + b
    dw = -(2/len(x)) * np.sum(x * (y - y_pred))
    db = -(2/len(x)) * np.sum(y - y_pred)
    w = w - learning_rate * dw
    b = b - learning_rate * db

# 输出最终参数
print(f"手动实现的斜率 (w): {w}")
print(f"手动实现的截距 (b): {b}")

# 可视化手动实现的拟合结果
y_pred_manual = w * x + b
plt.scatter(x, y)
plt.plot(x, y_pred_manual, color='green')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Manual Gradient Descent Fit')
plt.show()

5、最小二乘法最小二乘法通过最小化残差平方和（RSS）来求解最佳的w和b，其公式为： RSS=Σ(y_i-(w*x_i+b))^2通过对w和b求偏导并令其为0，可以得到解析解。

点击查看代码

import numpy as np
import matplotlib.pyplot as plt
# 样本数据
x = np.array([1, 2, 3, 4, 5], dtype=np.float)
y = np.array([1, 3.0, 2, 3, 5])
# 计算均值
x_mean = np.mean(x)
y_mean = np.mean(y)
# 计算回归系数
num = 0.0
d = 0.0
for x_i, y_i in zip(x, y):
   num += (x_i - x_mean) * (y_i - y_mean)
   d += (x_i - x_mean) ** 2
a = num / d
b = y_mean - a * x_mean
# 预测值
y_hat = a * x + b
# 绘图
plt.scatter(x, y)
plt.plot(x, y_hat, c='r')
plt.show()

六、线性回归的评估

1、评估模型性能的指标
R-Squared (R²)：衡量模型解释方差的比例。
Mean Squared Error (MSE)：衡量预测值与实际值之间的平均平方差。
Mean Absolute Error (MAE)：衡量预测值与实际值之间的平均绝对差。
（1）R-Squared（决定系数）衡量模型解释方差的比例。R-Squared值在0到1之间，值越接近1表示模型解释方差的比例越高。
在sklearn库中，可以通过r2_score函数计算R-Squared值：

点击查看代码

from sklearn.metrics import r2_score

# 计算R-Squared
r2 = r2_score(y_test, y_pred)
print(f"R-Squared: {r2}")

（2）Mean Squared Error（均方误差）衡量预测值与实际值之间的平均平方差。MSE值越小表示模型的预测误差越小。在sklearn库中，可以通过mean_squared_error函数计算MSE值：

点击查看代码

from sklearn.metrics import mean_squared_error

# 计算MSE
mse = mean_squared_error(y_test, y_pred)
print(f"Mean Squared Error: {mse}")

七、线性回归的优化

1、过拟合与欠拟合问题
过拟合和欠拟合是机器学习中常见问题，过拟合指的是模型过于复杂，对训练数据过于拟合，导致泛化能力差，欠拟合指的是模型过于简单，无法充分拟合训练数据，导致泛化能力也差。
解决过拟合的方法：
减少特征数量：选择最重要的特征。
正则化：通过L1或L2正则化减少模型复杂度。
解决欠拟合的方法包括：
增加特征数量：引入更多的特征。
增加模型复杂度：选择更复杂的模型。
2、正则化方法：L1正则与L2正则
正则化是一种减少模型复杂度的方法，通过在损失函数中加入正则化项来惩罚模型参数。两种常见方法包括：
L1正则：也称为Lasso正则化，通过绝对值范数惩罚模型参数。
L2正则：也称为Ridge正则化，通过平方范数惩罚模型参数。
在sklearn库中，可以通过Lasso和Ridge类实现L1和L2正则化：

点击查看代码

from sklearn.linear_model import Lasso, Ridge

# 创建Lasso模型
lasso_model = Lasso(alpha=0.1)

# 创建Ridge模型
ridge_model = Ridge(alpha=0.1)

# 训练模型
lasso_model.fit(X_train, y_train)
ridge_model.fit(X_train, y_train)

# 预测测试集数据
y_lasso_pred = lasso_model.predict(X_test)
y_ridge_pred = ridge_model.predict(X_test)

# 输出结果
print(f"Lasso预测房价: {y_lasso_pred}")
print(f"Ridge预测房价: {y_ridge_pred}")

posted on 2025-11-15 13:36 呦呵嘻嘻阅读(2) 评论(0) 收藏举报

刷新页面返回顶部

dyt-0812

公告

View Post

机器学习之线性回归模型