<数据结构><基础>几种平衡树————AVL trees,2-3trees,B-trees,B+-trees
1.AVL树
AVL树,是1962年由G. M. Adelson-Velsky和E. M. Landis共同提出的一种数据结构。AVL是作者名字的缩写。在二叉搜索树的基础上加上平衡的限制便是AVL树,所以AVL树也可以叫BBST,balanced binary search tree。因此,可以与有序序列对应是AVL树的基本性质。
——AVL树的单旋:(插入删除操作时)
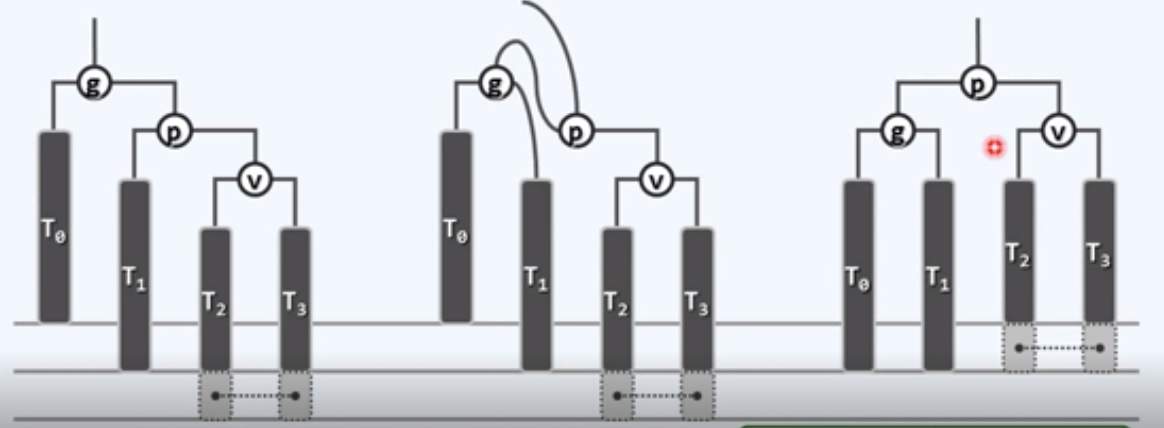
——AVL树的双旋:(插入删除操作时)
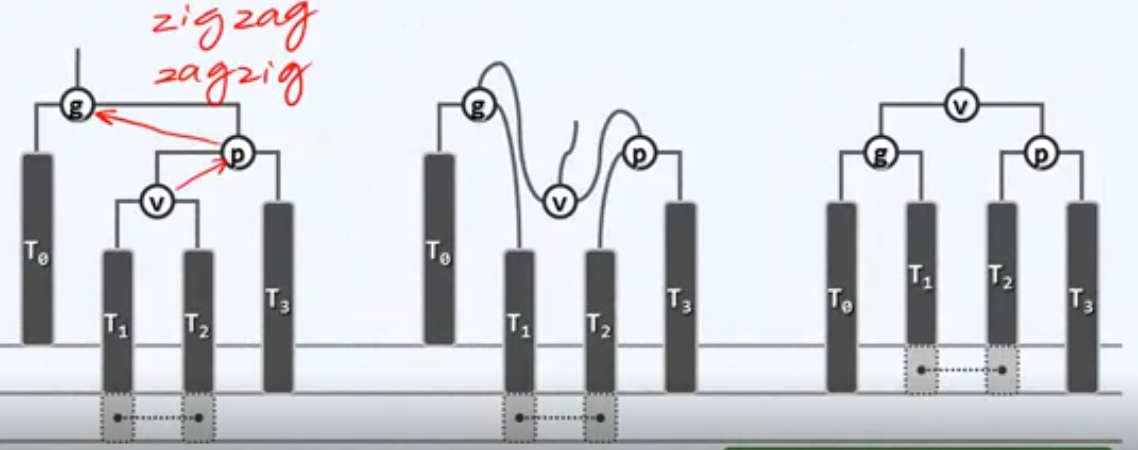
2.2-3树
2-3树的定义:
2-3树是一种naive的数据结构,是平衡树的一种,也是查找树的一种。
一棵由以下节点组成的树称为2-3树。
————2-节点:含有一个key和两条边,左边指向的2-3树中key都小于该节点,右边指向的2-3树中的key都大于该节点。
————3-节点:含有两个key和三条边,左边指向的2-3树中key都小于该节点,右边指向的2-3树中的key都大于该节点。
for example————————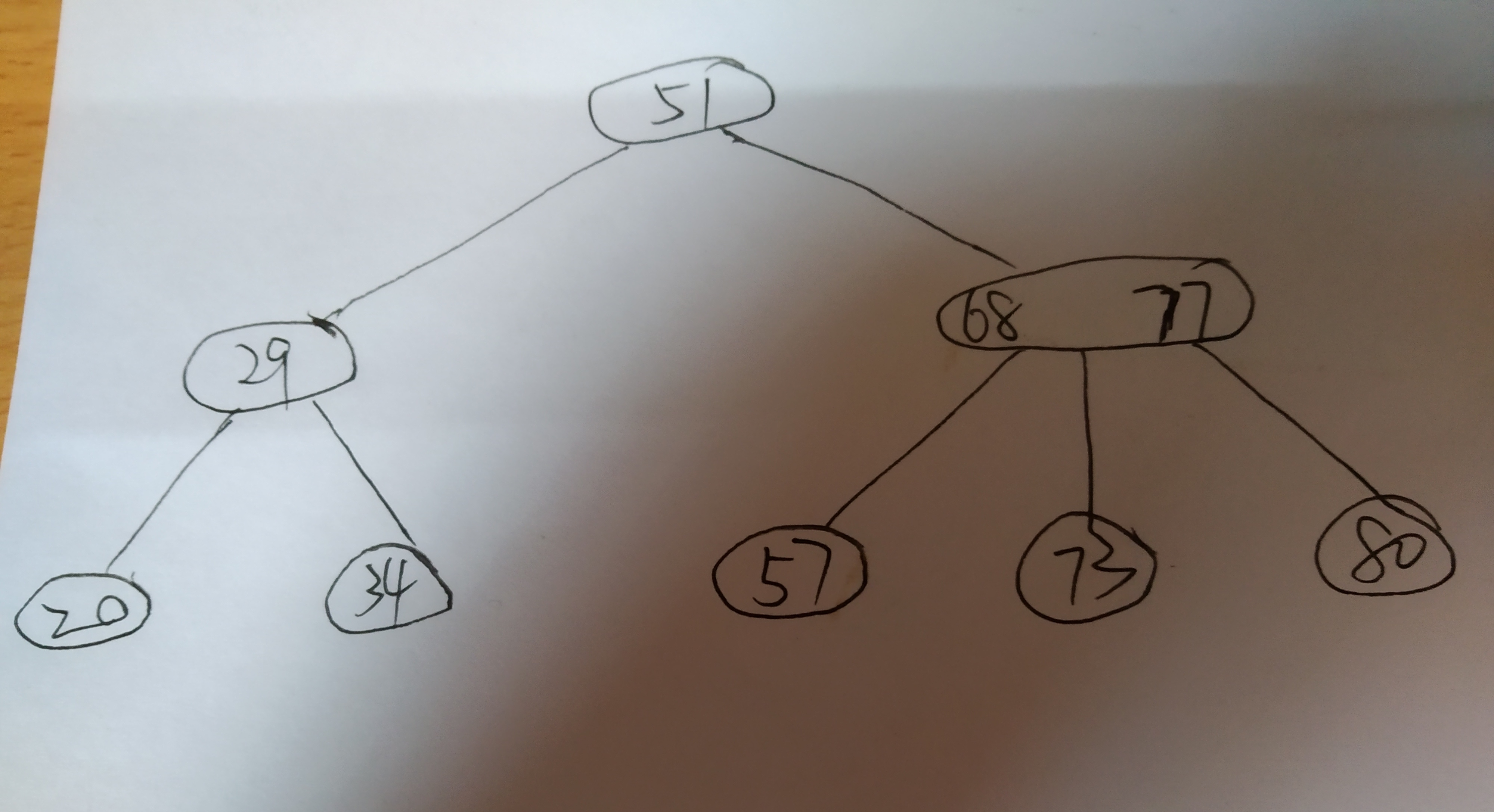
3.B-tree
B-tree从BBST平衡二叉搜索树发展而来。1970年R.Bayer和E.McCreight提出了一种平衡的多路搜索树结构,称为B-Tree。
这两位前辈试着将BST的每两代合并,如下:
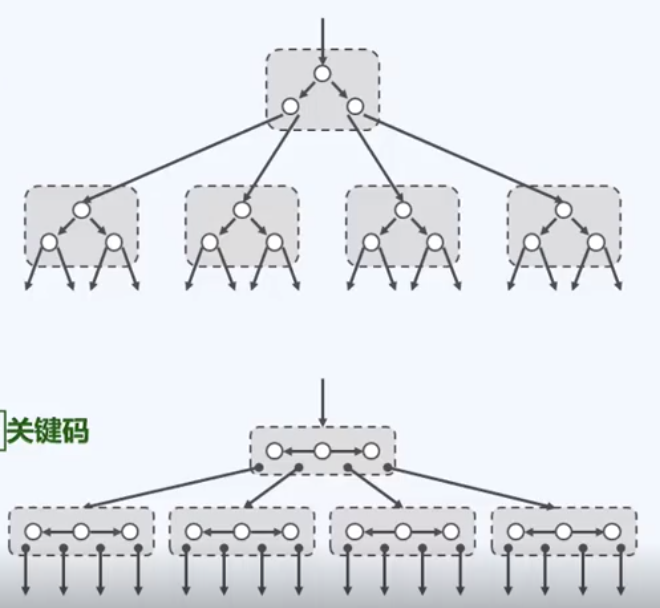
改完之后每个节点都有三个key,四个分支,可以叫这里的节点为超级节点。这是B-tree的由来。
同理,每3代合并,则7个key,8路;.......;每d代合并,则m-1个key,2d 路。
为什么AVL树不够用还弄个B-tree出来?这就是存储系统的问题了。多级存储系统中使用B-tree,可以针对外部查找大大减少I/O次数。AVL树每个节点只有一个key,而多路合并之后的B-tree每个节点含有一组key。如果有n=1G个记录,每次查找需要log(2,10^9)=30次I/O操作,AVL每次只读一个key得不偿失。B-tree的超级节点能批量访问,每次读一组。
从root到叶节点称为internal nodes(内部节点),所以internal nodes的底部是叶节点,叶节点的孩子称为external nodes(外部节点)。B树的高度是相对于外部节点而言的。

至此,对于一棵m路的B-tree:
每个内部节点的key个数在[m/2,m-1]之间。
root节点有2~m个分支,其他内部节点分支数在[ m/2,m ]之间。
e.g.:在一个5阶b树中,每个节点最多有4个key,最少有2个key。
在声明一个m阶B树时,对于每个非根非叶的内部节点,分配m个指针和m-1个key的空间。
for example————————

这棵b树的内部节点最多有4个,所以它是一棵5阶的b树。进而有以下限制————>每个内部节点的key数在[ m/2,m -1],每个非根非叶内部节点下面分支的数量不超过m。
B-tree的查找操作没必要再写了,只说一下B-tree的插入删除操作、
如果插入后节点key数超过m了,则认为出现了"上溢";插入——上溢——分裂
如果删除后节点key数小于m/2了(root节点是2),则认为出现了"下溢"。删除——下溢——旋转 /合并
B-tree的插入操作:(将k插入到树中)
1、首先作查找,如果k不存在于树中,则比较大小寻找插入位置,在叶子节点处结束,然后在叶子节点中插入该元素到有序位置。end。如果发生“上溢”则作步骤2的“分裂”。
2、将一半数量的keys分裂到新的其相邻右节点中,中间的key上溢到父节点中(如果父节点满了就递归“分裂”),end。如果根结点满了,则作步骤3
3、原来的根结点的中间的key向上移动到新的根结点中。
B-tree的删除操作:(删除树中的k)
1、首先作查找,找到k位于节点v中。如果v不是叶子节点,那就到k的右分支中一路沿着最左分支向下,如此最终抵达的节点u必然是k的直接后继,交换节点u和v的位置,现在v位于底部叶子层。删除节点v中的关键码k。如果发生”下溢“则进行2.中的旋转或合并操作。
2A、如果节点v恰好包含m/2-1个关键码和m/2-1个分支,则需要作旋转操作。
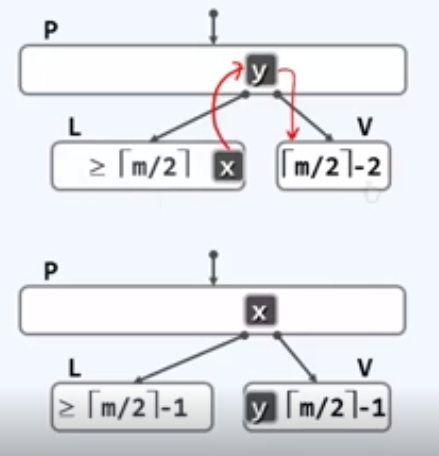
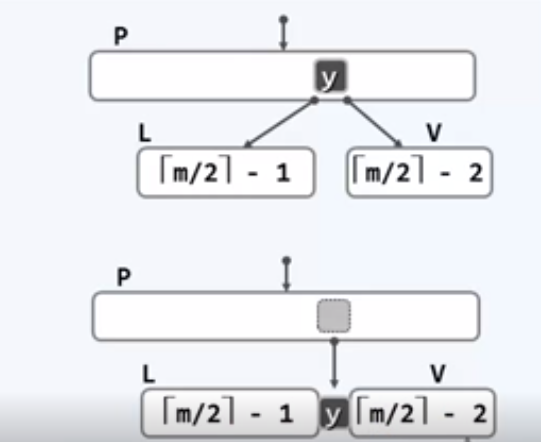
2B、如果L和R必有其一恰好含m/2-1个关键码(图示以L为例),则做合并操作。
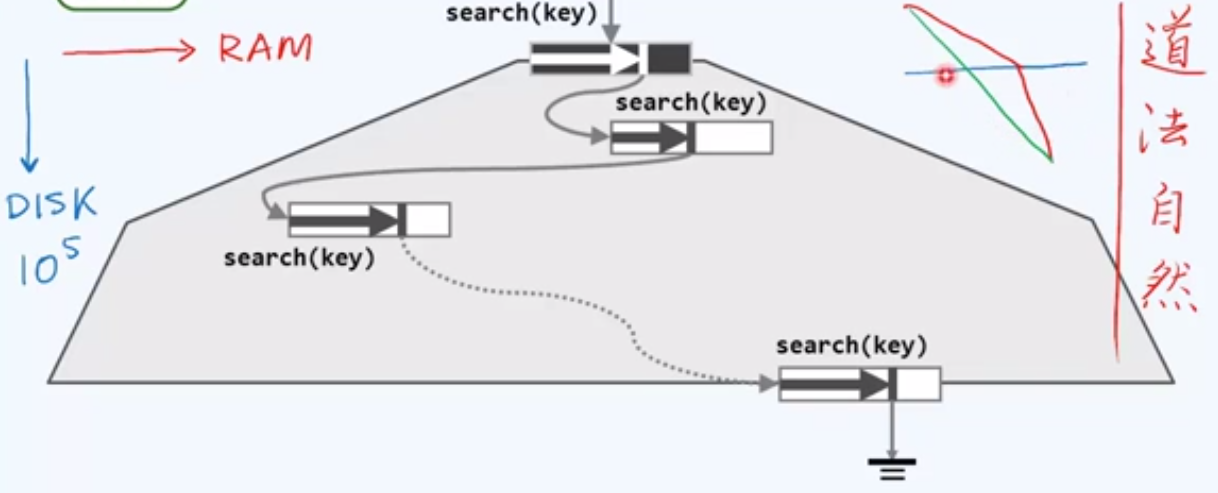
B树结构上体现的“道法自然”理念:
观察可见,B树有着又宽又矮的形状。这种设计是“道”。在存储系统中,RAM的I/O极快,而DISK的I/O较慢,两者可以差出5个数量级。这是“自然”。对B树内部节点内key的I/O类比RAM读写,而节点间的访问类比DISK读写。此之谓“道法自然”。
4.B+-tree
B+-tree的特点:
1.非叶子节点只存储键值信息
2.所有叶子节点之间都有一个链指针
3.数据记录都存放在叶子节点中
详细讲解:https://www.jianshu.com/p/71700a464e97
for example————————




 浙公网安备 33010602011771号
浙公网安备 33010602011771号