<反向传播(backprop)>梯度下降法gradient descent的发展历史与各版本
梯度下降法作为一种反向传播算法最早在上世纪由geoffrey hinton等人提出并被广泛接受。最早GD由很多研究团队各自独立提出来，可大都无人问津，而hinton做的研究完整表述了GD方法，同时hinton为自己的研究多次走动人际关系使得其论文出现在了当时的《nature》上，因此GD得到了第一次面向大规模受众的介绍。这为后面各种改进版GD的出现与21世纪深度学习的大爆发奠定了最重要的基础。
PART1：original版的梯度下降法
（下面关于梯度下降法的论述，我将使用直白浅显的语言）
首先已经有了 对weights和bias初始化过的神经网络计算图，也有一套训练集。
然后补充一下 具体training set 是如何投进去的：
如果我们训练集总共就几千个或者说不到几千个样本，那直接把它喂给神经网络就行（让m等于training set总样本数）。
但往往training set样本数是几万上百万的，这时一口气全部喂进去就太累了，我们往往采取分batch的方法投放数据集，即把数据集分成一撮撮（类比分治算法，类比一大堆草要剁，我把草分成一捆捆放到铡刀上）：
记每堆数据有m个样本，training set总样本数为M
当m=1时，也就是一次GD训练走一个样本，有点奢侈哈哈哈，称为随机(stochastic)梯度下降法。
此时cost function J(w,b,.......)=LOSS(y^,y)+正则化项
当m=M时，也就是一次GD训练走全部样本，称为batch梯度下降法。
此时cost function J(w,b,.......)=1/M * (全部Loss(y^(i),y(i))求和)+正则化项
当m介于两者之间时，称为minibatch梯度下降法。
这三种方法是最基础的梯度下降法，随机GD缺点是会失去向量化带来的加速，导致整体下来速度慢(当然它是单次训练最快的哈哈哈)，而且会跳上来跳下去的，不太喜欢它，在训练接近尾声时，它的结果并非完全收敛，而是波动的，这一点可通过动态增大减小learningrate来调节，另外随机GD可以用作在线学习，这算一个特色吧。batchGD缺点是训练总样本大时单次迭代时间太长导致整个训练过程耗时久，机子卡死，坑爹啊。所以一般我们都用minibatch法来跑GD，这样可以手动(也有自动调每个batch的m大小的，我就不在这写了)控制我们的GD。
可阅读1986年的经典之作：Learning internal representations by error-propagation， by David Rumelhart，GeoffreyHinton
PART2：进阶版GD--momentum动量梯度下降法
////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
在正式讲它之前，我们先介绍一种表示平均值的数学概念------滑动平均，也叫指数加权移动平均（Exponentially Weighted Moving Average）
现在有一组数据，需要找一个数来代表这组数据的平均水平，那么大多数人肯定想都不用想，所有数加起来然后除以数的个数,也可以叫做求期望。但是这种方法在计算机中并不友好。首先它需要一定的存储空间来保存这组数据，另外还要进行一次运算来算得平均数，如果数据量很大那么计算也会略有延时。为了克服这些问题，我们采用了一种新方法来表示一组数据的平均水平，即指数加权移动平均。
这里引入了一个新变量v与人设参数β。核心公式为 vt=β * vt-1 + (1-β) * θ t ，θ t 是当前第t个原始数据，以vt代表前t个数据的平均水平，vt-1 表示前t-1个数据的平均水平，β为更新参数，由人为指定。当β趋于1时v的走势趋于直线，跟原始数据的相关性弱；当β趋于0时v的走势趋于原始数据走势，跟原始数据的相关性强。如果有看过吴恩达cousera深度学习课程的同学肯定见过他举的气温变化例子的折线图，这里就不列出来了。 一般v0设置为0。
这一概念不仅在反向传播中有应用，RL领域中MC方法和TD方法更新Q(s,a)和V(s)的公式也是以EMA为基础提出的。可以说EMA在CS中应用广泛。
////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
使用PART1中的梯度下降法，必然会遇到一个问题：迭代的时候老是震荡，不能尽快收敛到最优点（如下图）。然而通过更改学习率a不能很好的解决这个问题。为了找到更牛逼的反向传播方法，开始有人把EMA用到GD迭代上，从而诞生了GD的改进版本---动量梯度下降法。
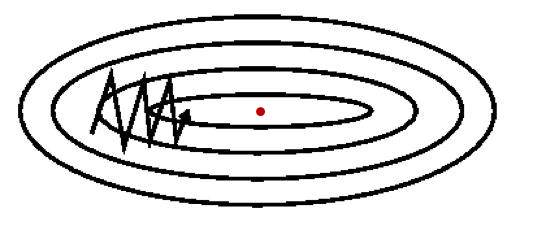
下面是momentumGD的参数更新方法：
vt = β * vt-1 + (1-β) * dwt
vt = β * vt-1 + (1-β) * dbt
w = w - a * vt
b = b - a * vt
这样通过引入动量v来预示最优点和当前位置的相对方向，便有效地遏制了之前更新过程中的震动，降低了整体优化耗时。（见下图）
温馨提示：momentum与SGD搭配使用更酸爽哦
PART3：momentum的改进版---NAG(Nesterov accelerated gradient)
这名字听起来逼格很高有没有。其实也没啥厉害的，就是在momentum基础上改动了一下，但是它确实加速了收敛。
下面是NAG的迭代公式：
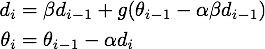
进一步推导，得到：
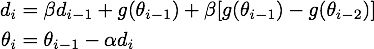
（其中d相当于momentum的v，θ则是要更新的参数，a是学习率）
从等价形式看，NAG在momentum基础上多了一个 β [ g(θi-1) - g(θ i-2 ) ] 。意义已经很明显了：如果这次梯度比上次梯度变大了，那么有理由相信它会继续大下去，如果这次梯度比上次梯度变小了，那么有理由相信它会继续小下去。是不是想起来了牛顿法？？没错，用的都是二阶导的思想。通过这一改动无疑成功加速了收敛。
下面这张图来自hinton的课程ppt，可以帮助理解，其中蓝线是momentum，绿线是NAG。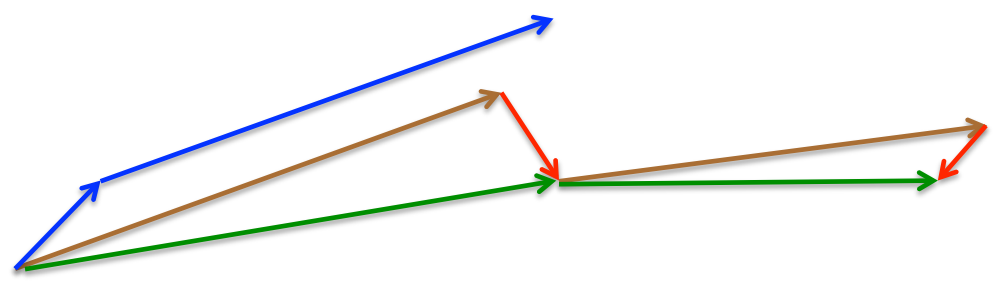
从全局收敛的视角对比momentum和NAG：（上面为momentum，下面为NAG）
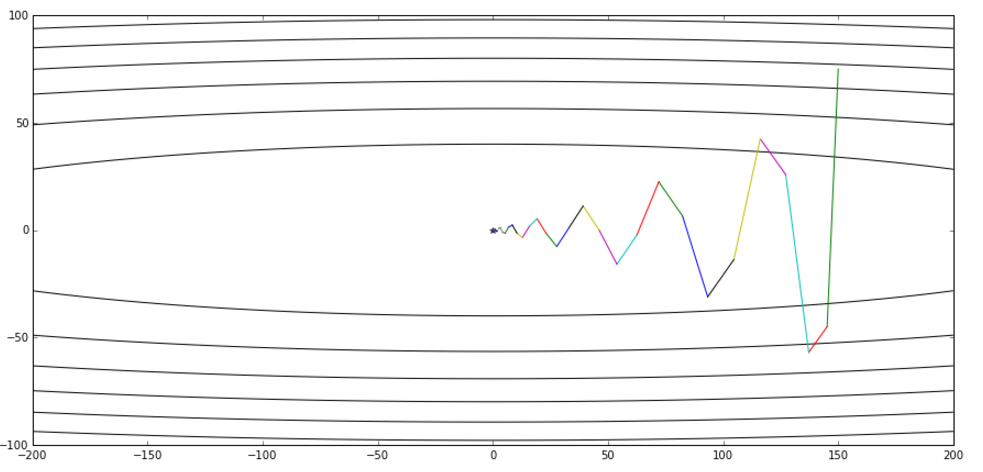
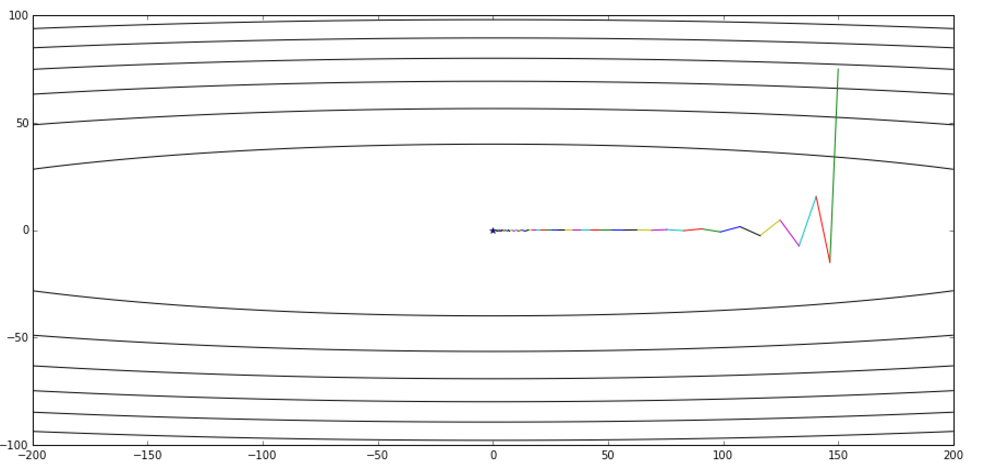
PART4：Adagrad与Adadelta
前面两个算法是在梯度更新上做了改动，下面要说的Adagrad与Adadelta则是在学习率上做了改动。Adagrad能自适应地为各个参数分配不同学习率，解决了不同参数应该使用不同更新速率的问题。
下面是Adagrad的更新公式：
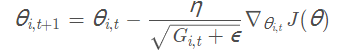
其中θ i,t 表示第i个参数第t次迭代时的值，η是人设学习率，Gi,t 是第i个参数到第t次迭代时的梯度累加量，Gi,t =Gi,t-1 + h * hT (其中h为当前参数的梯度向量)。ε是人为设定的辅助值，用来防止G为0时程序报错。
通过用
来代替之前静态的学习率a，我们达到了随迭代次数增加学习率减小的效果。Adagrad 在数据分布稀疏的场景能更好利用稀疏梯度的信息，相比 SGD能更有效地收敛。而它的缺点也十分明显，随着时间的增加，它的分母项越来越大，最终导致学习率收缩到太小无法进行有效更新。
在Adagra基础上，google的研究人员做了一些改进从而得到了Adadelta。
其对参数的更新方法如下：
下图是四种方法在mnist数据集上的对比图：
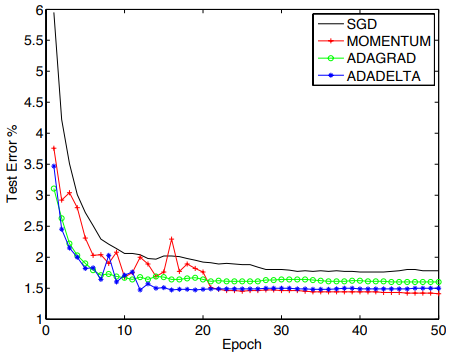
如果想进一步了解adadelta，可在此处查看原作：ADADELTA: An Adaptive Learning Rate Method
PART5：均方根传播(RMSprop)
RMSprop是hinton在他的课程中讲述的一种方法，跟上面说的Adadelta基本相似，
每次迭代中，针对待优化参数θ：
1、计算其梯度dθ ；
2、计算Sdθ =β * Sdθ + (1-β) * dθ2 ；
3、进行优化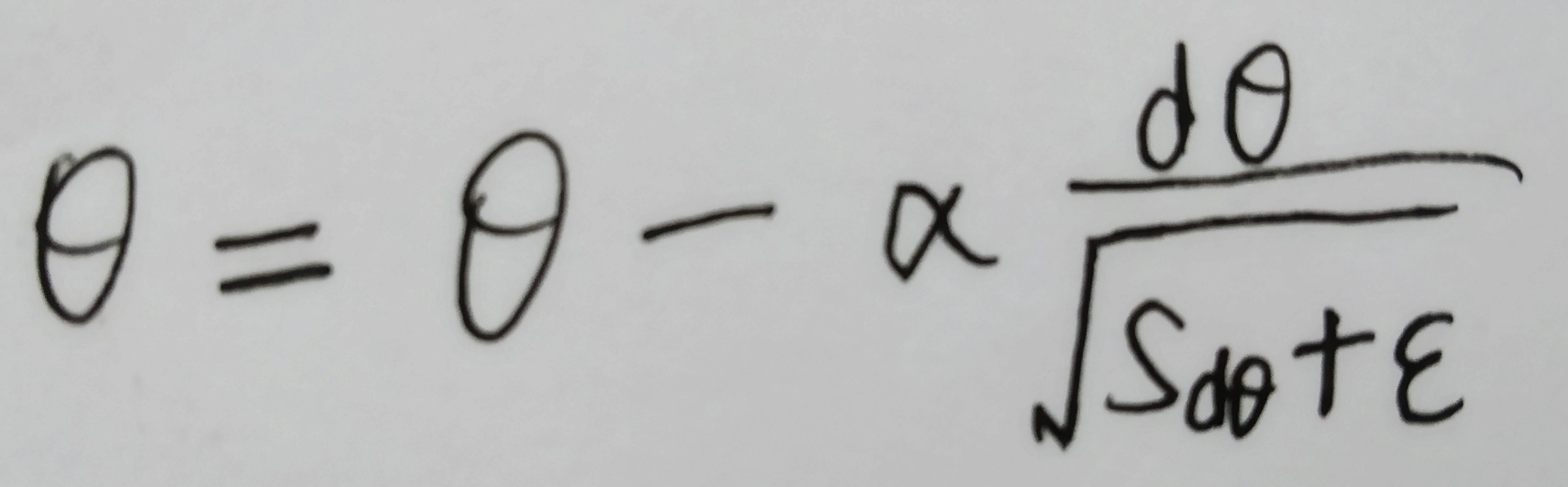
通过使用梯度平方的指数衰减学习率，RMSprop也对不同参数采用了不同更新速率。Hinton本人建议设置β为0.9，设置起始学习率a为0.001。
PART6：Adam
把RMSprop和momentum结合到一起，便得到了强大的‘、目前最常用的Adam优化方法。该方法由OpenAI 的 Diederik Kingma 和多伦多大学的 Jimmy Ba 在2015年提交到ICLR的论文Adam：a method for stochastic optimation 提出，相较于以上其他算法，该方法还有着很好的稀疏梯度和噪声问题处理能力。
算法实现步骤：
Adam 的默认超参数配置：
Adam的一大优点就是不怎么需要调参，此处只是对超参作一个简单说明和推荐设置。
- a：学习率或步长，它控制了权重的更新比率（如 0.001）。较大的值（如 0.3）在学习率更新前会有更快的初始学习，而较小的值（如 1.0E-5）会令训练收敛到更好的性能。
- β1：一阶矩估计的指数衰减率（如 0.9）。
- β2：二阶矩估计的指数衰减率（如 0.999）。该超参数在稀疏梯度（如在 NLP 或计算机视觉任务中）中应该设置为接近 1 的数。
- ε：最不重要但也不可或缺的超参数，其为了防止在实现中除以零（如 10E-8）。
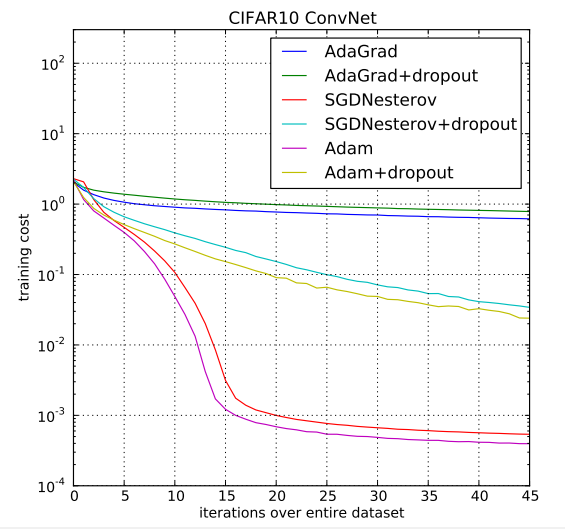
在CIFAR10数据集上，Adam和其他算法的表现：
PART7：AdaMAX
这是Adam的拓展版本。
在Adam中，单个参数的更新规则是将其梯度与当前和过去梯度的L2范数成反比例缩放。把这里的L2范数泛化到Lp范数也不是不可，尽管这里的变体会因为p值的变大而在数值上变得不稳定，但在特例中令p趋于无穷便得到了一个稳定又简单的算法。此时时间 t 时的步长和 vt^(1/p) 成反比例变化。
算法实现步骤：
AdaMax 参数更新的量级要比 Adam 更简单，|∆t| ≤ α。
=========================================================================
=========================================================================
最后放一个十分直观的汇总比较，该图像由Sebastian Ruder制作：
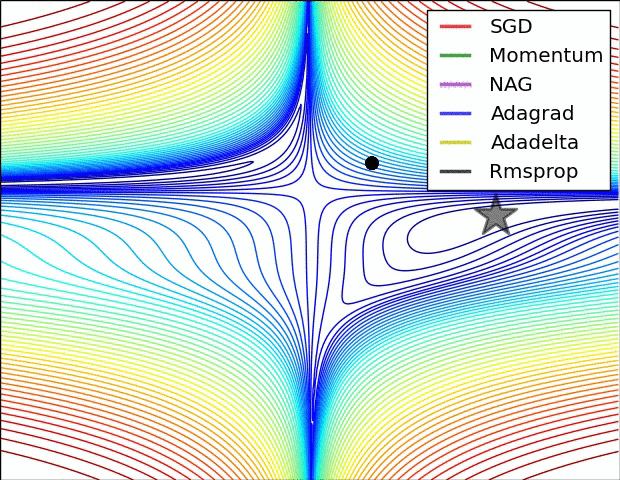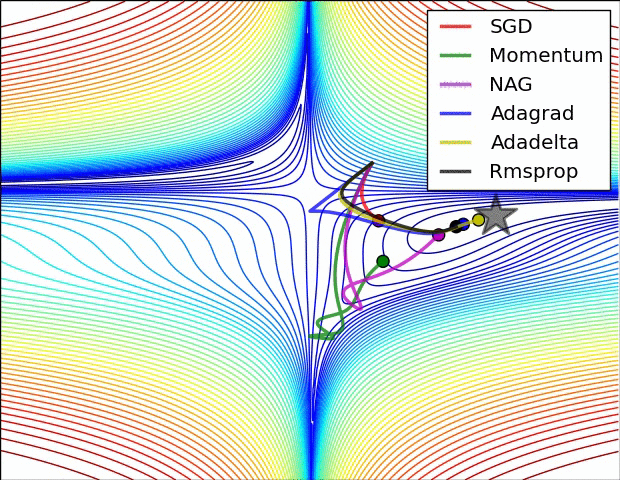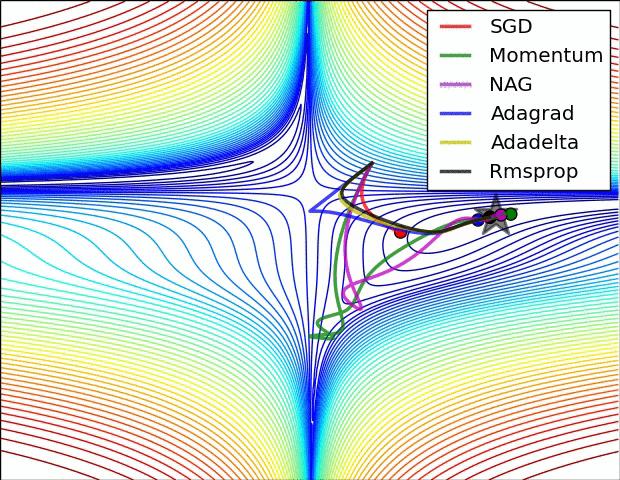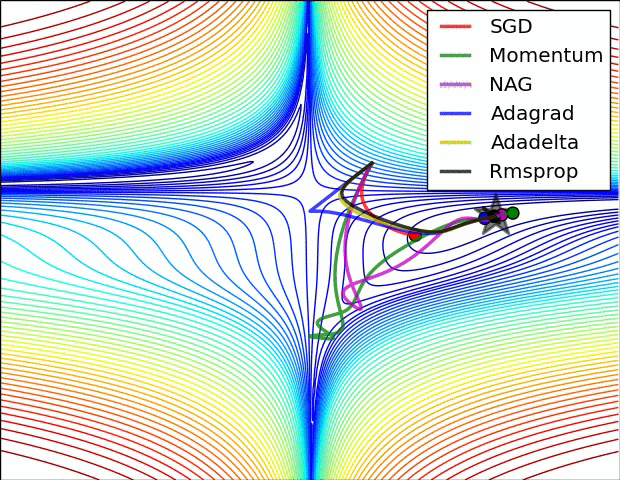
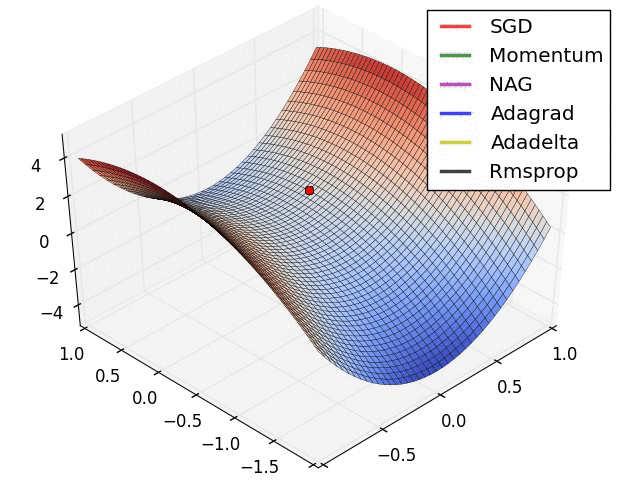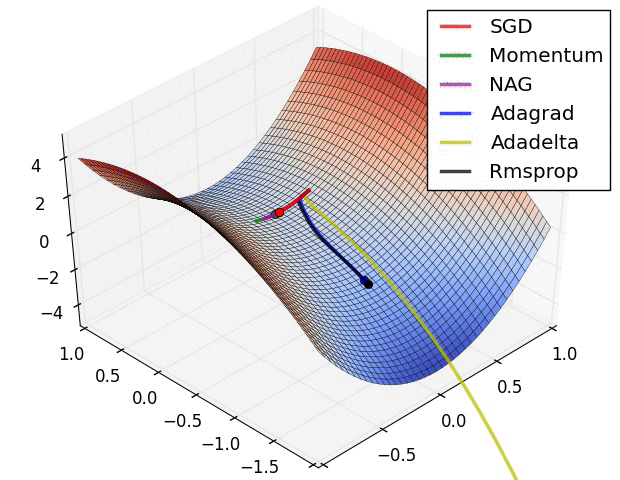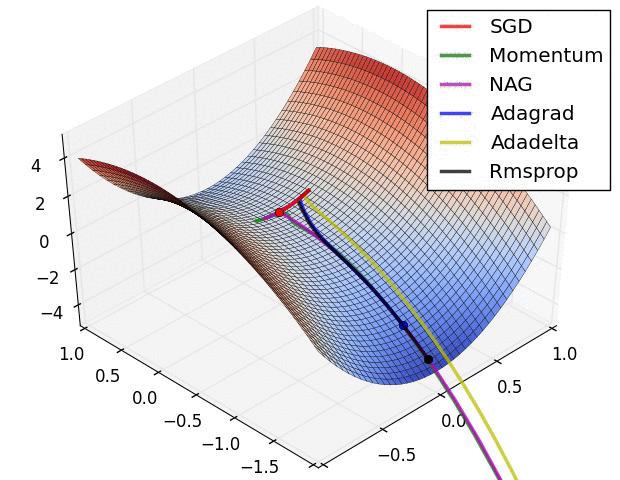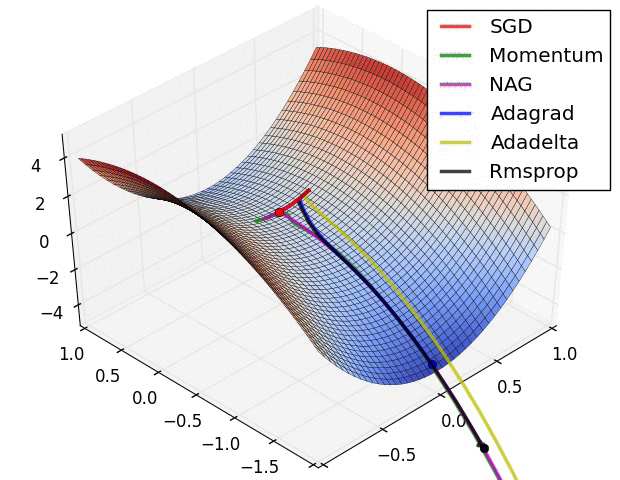
两幅图片来自Sebastian Ruder—An overview of gradient descent optimization algorithms
