[数学基础]奇异值分解SVD
之前看到过很多次奇异值分解这个概念,但我确实没有学过。大学线性代数课教的就是坨屎,我也没怎么去上课,后来查了点资料算是搞清楚了,现在写点东西总结一下。
奇异值分解,就是把一个矩阵拆成一组矩阵之和。在数学里面,因式分解,泰勒展开,傅里叶展开,特征值分解,奇异值分解都是这个路数。就是把当前数据表示成一组某种意义下互相独立的数据叠加的形式。目的在于简化计算处理或舍弃次要信息。
数学表达: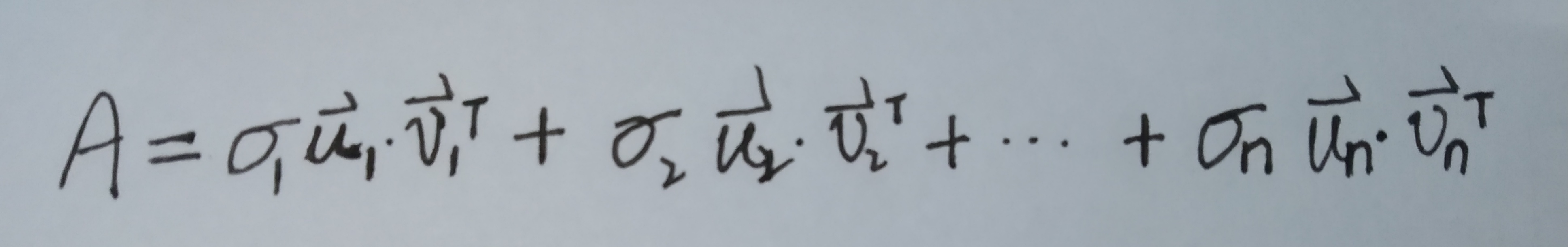 或
或
其中系数是每一项的奇异值,u,v是列向量,可以发现每一项的
都是秩为一的矩阵,我们人为假定
。跟矩阵特征值分解在形式上还是有很大相似之处的。
每个矩阵都可以表示成多个秩为一的矩阵的和,而每一项前的系数也就是奇异值的大小反映了这一项相对于A的权重大小。
然后说一下SVD的物理应用,主要举例图像压缩与图像去噪。
图像压缩,即适当降低图像精度,假设矩阵A表示了目标图片,对A作SVD分解,那么我们把A的分解式末端权重较小的部分舍弃(或者说只保留前面权重大的若干项),那么这张图片所需存储量便大大降低了,进而达到了图像压缩。
图像去噪,如果一副图像包含噪声,我们有理由相信那些较小的奇异值就是由噪声引起的。例如图像矩阵A奇异值分解后得到的奇异值为:15.29,7.33,5.23,4.16,0.24,0.03。最后两项相对于前面几项权重太小了,把它们舍掉,便直观地看出图像噪声减少了。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号