堆排序

堆排序是一种树形选择排序方法，它的特点是：在排序过程中，将 L[1...n] 看成一颗完全二叉树的顺序存储结构，利用完全二叉树的双亲结点和孩子结点之间的内在关系，在当前无序区中，选择关键字最大或最小元素。

堆的定义：

大根堆：一棵完全二叉树，满足任一节点都比其孩子节点大，即 L(i)=<L(2i) 且 L(i) =<L(2i+1)；
小根堆：一棵完全二叉树，满足任一节点都比其孩子节点小，即 L(i)>=L(2i) 且 L(i) >=L(2i+1) 。   　　（1=< i =<n/2）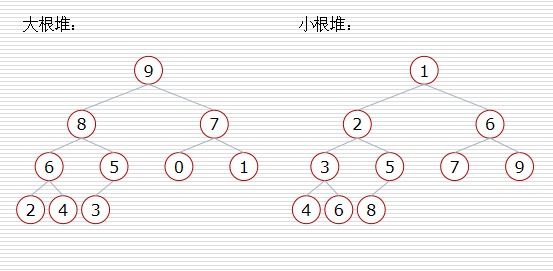

堆排序过程：

1、建立堆

2、得到堆顶元素，为最大元素

3、去掉堆顶，将堆最后一个元素放到堆顶，此时可通过一次调整重新使堆有序。
4、堆顶元素为第二大元素。

5、重复步骤3，直到堆变空。

 

 

自下往上逐步调整为大根堆：

 

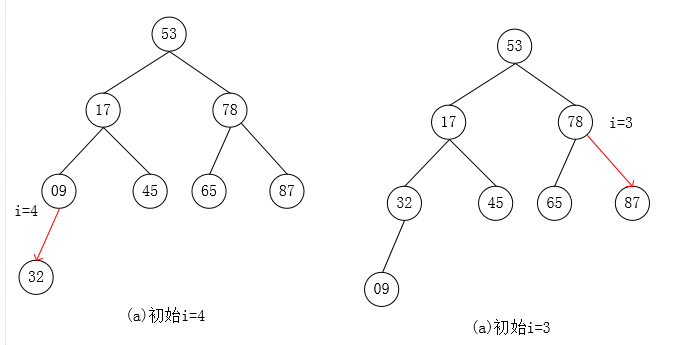
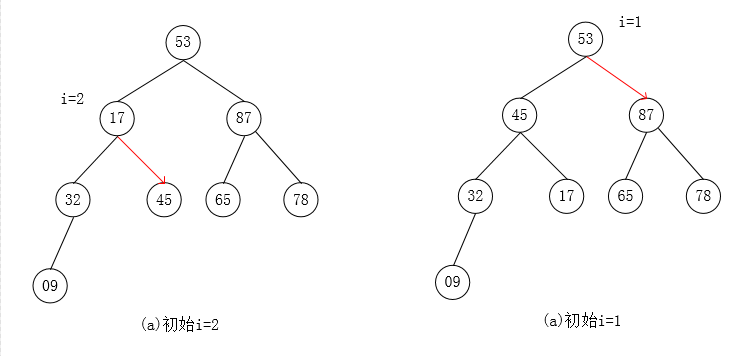
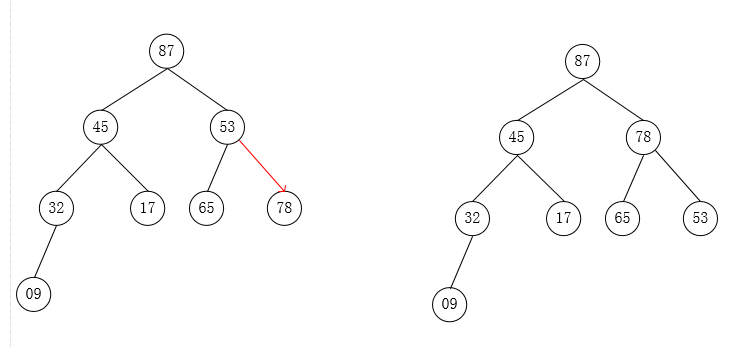
堆排序代码：

 

def sift(data, low, high):
    i = low
    j = 2 * i + 1
    tmp = data[i]
    while j <= high:    #孩子在堆里
        if j + 1 <= high and data[j] < data[j+1]:   #如果有右孩子且比左孩子大
            j += 1  #j指向右孩子
        if data[j] > tmp:   #孩子比最高领导大
            data[i] = data[j]   #孩子填到父亲的空位上
            i = j               #孩子成为新父亲
            j = 2 * i +1        #新孩子
        else:
            break
    data[i] = tmp           #最高领导放到父亲位置


def heap_sort(data):
    n = len(data)
    for i in range(n // 2 - 1, -1, -1):
        sift(data, i, n - 1)
    #堆建好了
    for i in range(n-1, -1, -1):            #i指向堆的最后
        data[0], data[i] = data[i], data[0] #领导退休，刁民上位
        sift(data, 0, i - 1)                #调整出新领导