D57 树的直径 树形DP+栈 P6118 [JOI 2019 Final] 独特的城市

D57 树的直径 树形DP+栈 P6118 [JOI 2019 Final] 独特的城市_哔哩哔哩_bilibili

 

P6118 [JOI 2019 Final] 独特的城市 / Unique Cities - 洛谷

给了一颗边权为 1 且节点有颜色（特产编号）的无根树。对于树上的每个节点，统计与该节点的距离唯一的点（友好点），且友好点中颜色不同的个数。

思路

直径性质：树上距离最远的点必然都在直径的端点上。

观察可知：到节点 x 的距离唯一的点（友好点），一定在 从 x 出发的最长路上。

如图，到节点 6 的距离唯一的点（友好点）是 4 和 1，5 被 7 毙掉，3、2 被 8、9 毙掉。

                                             

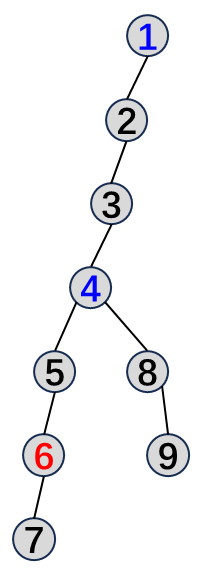
我们先找出一条直径的两个端点，把直径的一端提起做树根。我们先求每个点到树根的路径上有多少点是友好点。

我们看到一个点下面挂着的最长链和次长链对友好点的统计起决定作用。例如，节点 4 的次长链会毙掉 其长儿子的若干友好点，节点 4 的最长链会毙掉 4 的若干友好点。

我们先树形DP，预处理出每个点的最长链、次长链、长儿子、深度。

我们再从根遍历，计算答案的流程如下：

1. 加入 x 的父节点.
2. 把到当前点 x 的距离 $≤$ 次长链的点毙掉，这些点就不会给 x 的长儿子贡献答案.
3. 先遍历长儿子.
4. 把到当前点 x 的距离 $≤$ 最长链的点毙掉，这些点就不会给当前点 x 贡献答案.
5. 后遍历短儿子.
6. 更新答案.
7. 删除 x 的父节点，恢复现场.

我们把直径的左端提起做根，计算一遍答案。再把直径的右端提起做根，计算一遍答案。两遍的答案取最大。
如图，节点旁边的数字表示本次遍历完成后其友好点的个数。因为自顶向底算，所以需要正反两遍。

                                                  

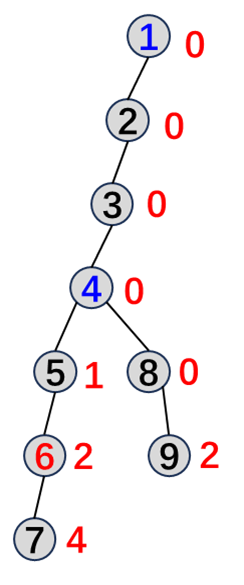
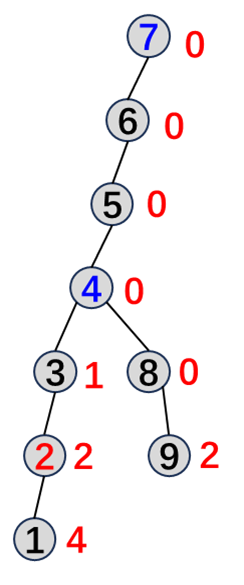
我们用栈维护友好点的个数，同时，用桶维护友好点的颜色。如果该节点颜色是第一次出现，答案个数 $+1$；如果该节点颜色消失，答案个数 $-1$。

// 树的直径 树形DP+栈 O(n)
#include<bits/stdc++.h>
using namespace std;

const int N=200010;
int n,m,c[N];
int h[N],to[N<<1],ne[N<<1],idx;
void adde(int x,int y){
  to[++idx]=y,ne[idx]=h[x],h[x]=idx;
}

int d[N],p,l,r;
void dfs1(int x,int fa){
  if(d[x]>d[p]) p=x;
  for(int i=h[x];i;i=ne[i]){
    int y=to[i];
    if(y!=fa){
      d[y]=d[x]+1; //记录从根到y的距离
      dfs1(y,x);
    }
  }
}
int dep[N],d1[N],d2[N],son[N];
void dfs2(int x,int fa){ //树形DP
  dep[x]=dep[fa]+1,d1[x]=d2[x]=0,son[x]=0;
  for(int i=h[x];i;i=ne[i]){
    int y=to[i];
    if(y!=fa){
      dfs2(y,x);
      if(d1[x]<d1[y]+1) d2[x]=d1[x],d1[x]=d1[y]+1,son[x]=y;
      else if(d2[x]<d1[y]+1) d2[x]=d1[y]+1;
    }
  }
}
int stk[N],top,num[N],res,ans[N];
void add(int x){++num[c[x]]; if((num[c[x]])==1)res++;} //加入点的贡献
void del(int x){--num[c[x]]; if((num[c[x]])==0)res--;} //删除点的贡献
void dfs3(int x,int fa){
  if(fa) add(stk[++top]=fa); //加入父节点
  while(top && dep[x]-dep[stk[top]]<=d2[x]) del(stk[top--]); //删除上面长度≤次长链的节点
  if(son[x]) dfs3(son[x],x); //先遍历长儿子
  while(top && dep[x]-dep[stk[top]]<=d1[x]) del(stk[top--]); //删除上面长度≤最长链的节点
  for(int i=h[x];i;i=ne[i]){ //后遍历短儿子
    int y=to[i];
    if(y!=fa&&y!=son[x]) dfs3(y,x);
  }
  ans[x]=max(ans[x],res); //更新答案
  if(stk[top]==fa) del(stk[top--]); //删除父节点，恢复现场
}
int main(){
  cin>>n>>m;
  for(int i=1,x,y;i<n;i++){
    cin>>x>>y;
    adde(x,y),adde(y,x);
  }
  for(int i=1;i<=n;i++) cin>>c[i];
  
  dfs1(1,0); l=p; d[p]=0;
  dfs1(p,0); r=p; //记录直径端点
  
  dfs2(l,0); //左端进入，记录深度、最长链、次长链、长儿子
  dfs3(l,0); //计算答案
  memset(num,0,sizeof(num)); //清空桶
  top=res=0; //清空栈
  dfs2(r,0); //右端进入，记录深度、最长链、次长链、长儿子
  dfs3(r,0); //计算答案
  for(int i=1;i<=n;i++) cout<<ans[i]<<"\n";
}