D54 树的直径 三次DFS P4408 [NOI2003] 逃学的小孩

D54 树的直径 三次DFS P4408 [NOI2003] 逃学的小孩_哔哩哔哩_bilibili

 

P4408 [NOI2003] 逃学的小孩 - 洛谷

在一棵无根树上，找 A,B,C 三个点，从 C 点出发，走 min(CA,CB)+AB 这样的路径。问最坏情况下，路径长度的最大值。

思路

既然 AB 是必走的一条路径，我们贪心地取树的直径。然后统计 max(min(CA,CB)) 即可。

                                

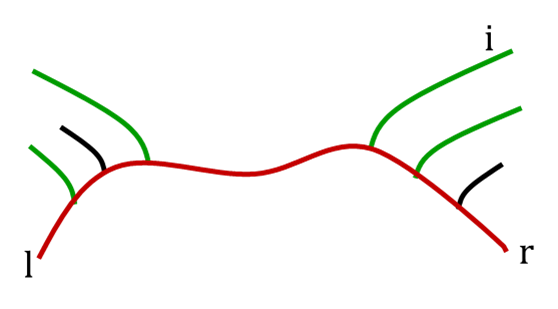
先两次 DFS 求出 d1为直径，p为直径的右端点。此时 d 数组记录了各点到直径左端点的距离。 

用 dd 数组复制一遍 d 数组，保存各点到直径左端点的距离。

再跑一遍 DFS，此时 d 数组记录了各点到直径右端点的距离。

最后枚举一遍各点到直径两端点的最小值的最大值，用 d2=max(d2,min(dd[i],d[i])) 记录。

答案当然是 d1+d2。

// 树的直径 三次DFS O(n)
#include<bits/stdc++.h>
#define int long long
using namespace std;

const int N=200010;
int h[N],idx;
struct edge{int to,w,ne;} e[N<<1];
void add(int x,int y,int z){
  e[++idx]={y,z,h[x]}; h[x]=idx;
}
int n,m,d[N],dd[N],p,d1,d2;

void dfs(int x,int fa){
  if(d[p]<d[x]) p=x;
  for(int i=h[x];i;i=e[i].ne){
    int y=e[i].to;
    if(y!=fa){
      d[y]=d[x]+e[i].w;
      dfs(y,x);
    }
  }
}
signed main(){
  scanf("%lld%lld",&n,&m);
  for(int i=1,x,y,z;i<=m;i++){
    scanf("%lld%lld%lld",&x,&y,&z);
    add(x,y,z);add(y,x,z);
  }
  dfs(1,0); d[p]=0;
  dfs(p,0); d1=d[p]; //d1为直径，p为直径的右端点
  for(int i=1;i<=n;i++) dd[i]=d[i]; //dd保存各点到直径左端的距离
  d[p]=0; dfs(p,0);  //d记录各点到直径右端的距离
  for(int i=1;i<=n;i++) d2=max(d2,min(d[i],dd[i])); //更新距离两端点最小值的最大值
  printf("%lld\n",d1+d2);
}