D56 树的直径 两次DFS+双指针 P3761 [TJOI2017] 城市

D56 树的直径 两次DFS+双指针 P3761 [TJOI2017] 城市_哔哩哔哩_bilibili

 

P3761 [TJOI2017] 城市 - 洛谷

给了一颗 n 个点的带边权的无根树，你选择一条边删除，再用一条等权边连接两颗树，使得新树的直径最小。输出该直径。

思路

因为 n=5000，O(n²) 的做法不难想。

我们可以暴力枚举断边，然后 DFS 出两颗树的直径。

• 当通过在两棵树 $x,y$ 间连一条边以合并为一棵树时，连接两棵树的中心可以使新树的直径最小。
• 新树的直径 $=max(x 的半径+y的半径+1，x 的直径，y的直径)$。

每次更新答案，取最小值。

可以参考：E34 树形DP 树的中心 - 董晓 - 博客园

// 树的直径 树形DP 暴力 O(n^2)
#include<bits/stdc++.h>
using namespace std;

const int N=5010;
int h[N],idx=1;
struct edge{int to,w,ne;} e[N<<1];
void add(int x,int y,int w){
  e[++idx]={y,w,h[x]}; h[x]=idx;
}
int n,d1[N],d2[N],son[N],up[N],mxd,ans=1e9;
bool col[N<<1];

void dfs1(int x,int fa){ //树形DP 求直径
  for(int i=h[x];i;i=e[i].ne){
    int y=e[i].to,w=e[i].w;
    if(y!=fa&&!col[i]){
      dfs1(y,x);
      if(d1[x]<d1[y]+w) d2[x]=d1[x],d1[x]=d1[y]+w,son[x]=y; //x下挂的最长链、次长链，x最长链的儿子
      else if(d2[x]<d1[y]+w) d2[x]=d1[y]+w;
    }
  }
  mxd=max(mxd,d1[x]+d2[x]); //直径=最长链+次长链
}
void dfs2(int x,int fa){ //类似树的中心求法 求半径
  for(int i=h[x];i;i=e[i].ne){
    int y=e[i].to,w=e[i].w;
    if(y!=fa&&!col[i]){
      if(son[x]==y) up[y]=max(up[x],d2[x])+w; //y上方的最长距离=max(x上方的最长距离+w(x,y)，x的次长链+w(x,y))
      else up[y]=max(up[x],d1[x])+w; //y上方的最长距离=x的最长链+w(x,y)
      dfs2(y,x);
    }
  }
  mxd=min(mxd,max(up[x],d1[x])); //半径=min{max{x上方的最长距离,x的最长链}}
}
int main(){
  scanf("%d",&n);
  for(int i=1,x,y,w;i<n;i++){
    scanf("%d%d%d",&x,&y,&w);
    add(x,y,w);add(y,x,w);
  }
  for(int i=2,zjx,zjy,bjx,bjy;i<=idx;i+=2){ //枚举边
    memset(d1,0,sizeof d1);
    memset(d2,0,sizeof d2);
    memset(up,0,sizeof up);
    memset(son,0,sizeof son);        
    int x=e[i].to,y=e[i^1].to,w=e[i].w;
    col[i]=col[i^1]=1; //断边染色
    mxd=0; dfs1(x,0); zjx=mxd;
    mxd=0; dfs1(y,0); zjy=mxd;
    mxd=1e9; dfs2(x,0); bjx=mxd;
    mxd=1e9; dfs2(y,0); bjy=mxd;
    ans=min(ans,max(max(zjx,zjy),bjx+bjy+w)); //最大直径的最小值
    col[i]=col[i^1]=0; //断边去色
  }
  printf("%d",ans);
}

 

优化

我们可以利用直径的性质和问题的单调性，配合双指针优化为 $O(n)$。

我们一定选直径上的一条边删除，才能使得连边后的新树的直径更短。

删除直径上的一条边，得到左右两颗树 A 和 B。原树直径的端点仍然是分割后树 A 和 树 B 的直径的一端。

如图，绿色为直径。我们沿着原直径，先从左向右搜索，

我们发现直径长度和半径长度都是单调不减的，子树直径的中心也必然在原直径上，且单调右移。

我们用快指针 $i$ 枚举原直径上的点，慢指针 $c$ 枚举中心点的移动。

指针 $i$ 走到第 3 个点时，左树的直径为 13，中心 $c$ 在第 2 个点上，半径为 10。

指针 $i$ 走到第 4 个点时，左树的直径为 25，中心 $c$ 在第 4 个点上，半径为 13。

为了避免重复搜索，可以对搜过的子树打上标记。

           

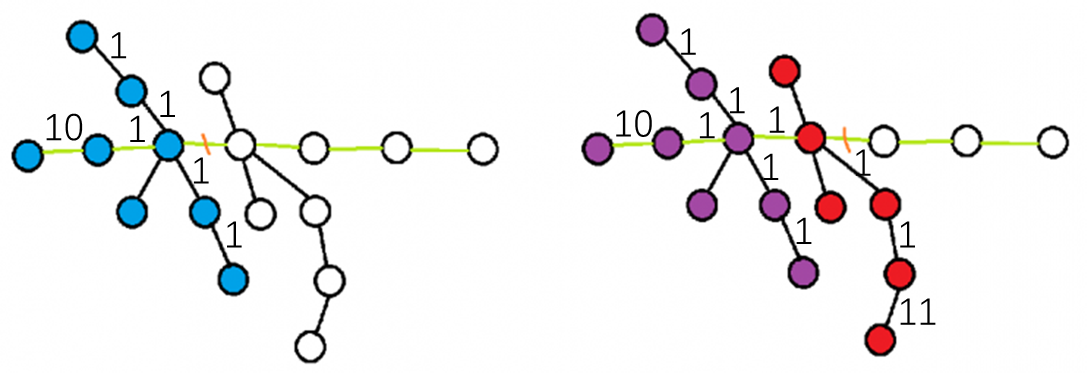
再从右向左搜索，记录以直径上的点为根的子树的直径和半径。最后通过左右两颗树的直径和半径拼凑答案。

// 树的直径 树形DP+双指针 O(n)
#include<bits/stdc++.h>
using namespace std;

const int N=5005;
int h[N],idx;
struct edge{int to,w,ne;}e[N<<1];
void add(int x,int y,int z){
  e[++idx]={y,z,h[x]}; h[x]=idx;
}

int n,d[N],pre[N],col[N],p,cnt;
int zv[N],zw[N]; //直径上的点和边权
struct Tree{
  int d,r;       //子树的直径和半径
}T1[N],T2[N];

void dfs1(int u,int fa){
  if(d[p]<d[u]) p=u; //更新端点
  pre[u]=fa;
  for(int i=h[u];i;i=e[i].ne){
    int v=e[i].to;
    if(v!=fa){
      d[v]=d[u]+e[i].w; //记录根到v的距离
      dfs1(v,u);
    }
  }
}
void dfs2(int u,int fa){
  for(int i=h[u];i;i=e[i].ne){
    int v=e[i].to,w=e[i].w;
    if(v!=fa && col[v]){
      zv[++cnt]=v; //记录直径上的点
      zw[cnt]=w;   //记录直径上的边权
      dfs2(v,u);
    }
  }
}
void dfs3(int u,int &s){
  s=max(s,d[u]);
  for(int i=h[u];i;i=e[i].ne){
    int v=e[i].to,w=e[i].w;
    if(!col[v]){ //只能走直径之外没遍历的点
      col[v]=1;
      d[v]=d[u]+w; //直径端点到v的距离
      dfs3(v,s);
    }
  }
}
int main(){
  scanf("%d",&n);
  for(int i=1,x,y,z;i<n;i++){
    scanf("%d%d%d",&x,&y,&z);
    add(x,y,z); add(y,x,z);
  }
  dfs1(1,0); d[p]=0;
  dfs1(p,0); //记录直径的端点p
  
  for(int i=p;i;i=pre[i]) col[i]=1; //标记直径的点
  zv[++cnt]=p; //记录直径的起点
  dfs2(p,0);   //记录直径上的点和边权
  
  memset(d,0,sizeof(d));
  int c=1;
  for(int i=2;i<=cnt;i++){ //考虑左子树
    d[zv[i]]=d[zv[i-1]]+zw[i]; //从端点l到i的距离
    int s=0;
    dfs3(zv[i],s);    //s=从端点l到i再到i的最长支路的距离
    if(s<=T1[zv[i-1]].d) T1[zv[i]]=T1[zv[i-1]]; //s小，就继承
    else{
      T1[zv[i]].d=s; //用 s 更新直径
      while(c<i&&max(d[zv[c]],s-d[zv[c]])>max(d[zv[c+1]],s-d[zv[c+1]])) c++; //中心在原直径上，只要偏沉就右移
      T1[zv[i]].r=max(d[zv[c]],s-d[zv[c]]); //用端点l到新中心的距离d和s-d，更新半径
    }
  }

  memset(col,0,sizeof(col));
  for(int i=p;i;i=pre[i]) col[i]=1; //标记直径的点    
  memset(d,0,sizeof(d));
  c=cnt;
  for(int i=cnt-1;i>=1;i--){ //考虑右子树
    d[zv[i]]=d[zv[i+1]]+zw[i+1];
    int s=0; 
    dfs3(zv[i],s);
    if(s<=T2[zv[i+1]].d) T2[zv[i]]=T2[zv[i+1]];
    else{
      T2[zv[i]].d=s;
      while(c>i&&max(d[zv[c]],s-d[zv[c]])>max(d[zv[c-1]],s-d[zv[c-1]])) c--;
      T2[zv[i]].r=max(d[zv[c]],s-d[zv[c]]);
    }
  }
  
  int ans=1e9;
  for(int i=1;i<cnt;i++) ans=min(ans,max(T1[zv[i]].r+T2[zv[i+1]].r+zw[i+1], max(T1[zv[i]].d,T2[zv[i+1]].d)));
  printf("%d",ans);
}