D53 树的直径 建图技巧+两次DFS P2610 [ZJOI2012] 旅游

D53 树的直径 建图技巧+两次DFS P2610 [ZJOI2012] 旅游_哔哩哔哩_bilibili

 

P2610 [ZJOI2012] 旅游 - 洛谷

一个凸 n 边形，划分成为三角剖分。不能走周围边，只能走中间的剖分边。问走完一条简单路径，最多有多少个三角形，其边在路径上。

思路

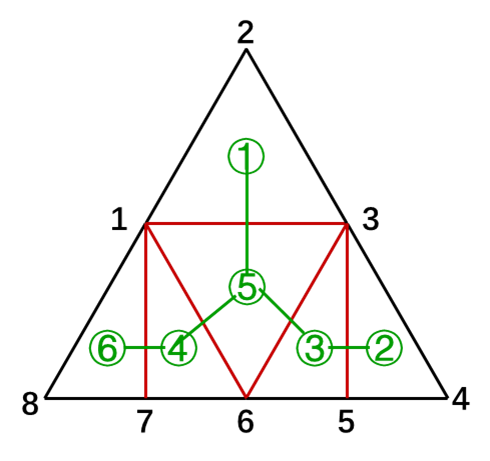
如图，是一个凸 8 边形（我只是省事，没有让各点外凸，不影响看图）。红色边是相邻三角形的邻边，是可走边。

如果把每个三角形缩成一个点，相邻的点连边，显然构成一颗树，树边与红色边一一对应。

所走红边的最长路径等于树的直径。

答案是直径上的点数 $=$ 边数 $+1$。

                                      

建图技巧

枚举三角形的编号，编号做树的节点。

三角形顶点 ${p,q,r}$  升序排列，免去判重。

然后依次枚举三角形的三条边，
如果当前边未遍历，则用当前三角形的编号标记。
如果当前边已遍历，说明当前三角形与已遍历过的三角形相邻，则把两三角形的编号用树边相连。

// 树的直径 建图技巧+两次DFS O(n)
#include<bits/stdc++.h>
using namespace std;

const int N=200005;
int h[N],to[N<<1],ne[N<<1],idx;
void add(int a,int b){
  to[++idx]=b; ne[idx]=h[a]; h[a]=idx;
  to[++idx]=a; ne[idx]=h[b]; h[b]=idx;
}
int n,d[N],p,ans;
map<pair<int,int>,int> mp;

void dfs(int x,int f){
  if(d[x]>d[p]) p=x; //记录直径的端点
  for(int i=h[x];i;i=ne[i]){
    int y=to[i];
    if(y!=f){
      d[y]=d[x]+1;   //记录从根到y的距离
      dfs(y,x);
    }
  }
}
int main(){
  ios::sync_with_stdio(0);cin.tie(0);
  cin>>n;
  for(int i=1,p,q,r;i<=n-2;++i){ //枚举三角形的编号，编号做树的节点
    cin>>p>>q>>r;
    if(p>q) swap(p,q);
    if(p>r) swap(p,r);
    if(q>r) swap(q,r);          //三角形顶点{p,q,r}升序排列，免去判重
    if(!mp[{p,q}]) mp[{p,q}]=i; //若当前边未遍历，则用当前三角形的编号标记
    else add(i,mp[{p,q}]);      //若当前边已遍历，说明当前三角形与已遍历过的三角形相邻，则把两三角形的编号用树边相连
    if(!mp[{p,r}]) mp[{p,r}]=i;
    else add(i,mp[{p,r}]);
    if(!mp[{q,r}]) mp[{q,r}]=i;
    else add(i,mp[{q,r}]);
  }
  dfs(1,0); d[p]=0;
  dfs(p,0); ans=d[p]+1; //答案是直径上的点数=边数+1
  cout<<ans;
}