E100 区间DP+拉插优化 P5469 [NOI2019] 机器人

视频链接：

 

 

 

 

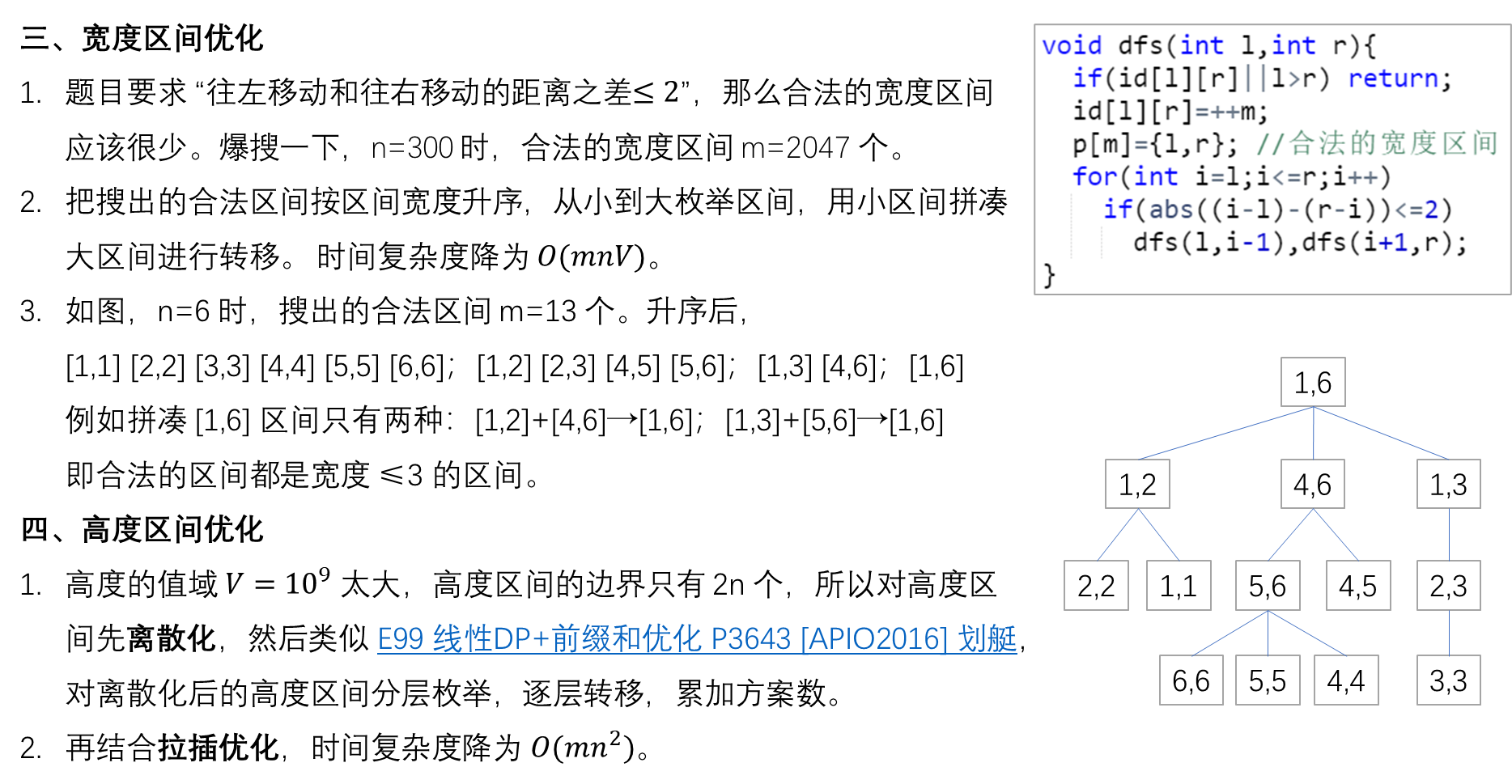
参考：E99 线性DP+前缀和优化 P3643 [APIO2016] 划艇 - 董晓 - 博客园

参考：G75 拉插 CF622F The Sum of the k-th Powers - 董晓 - 博客园

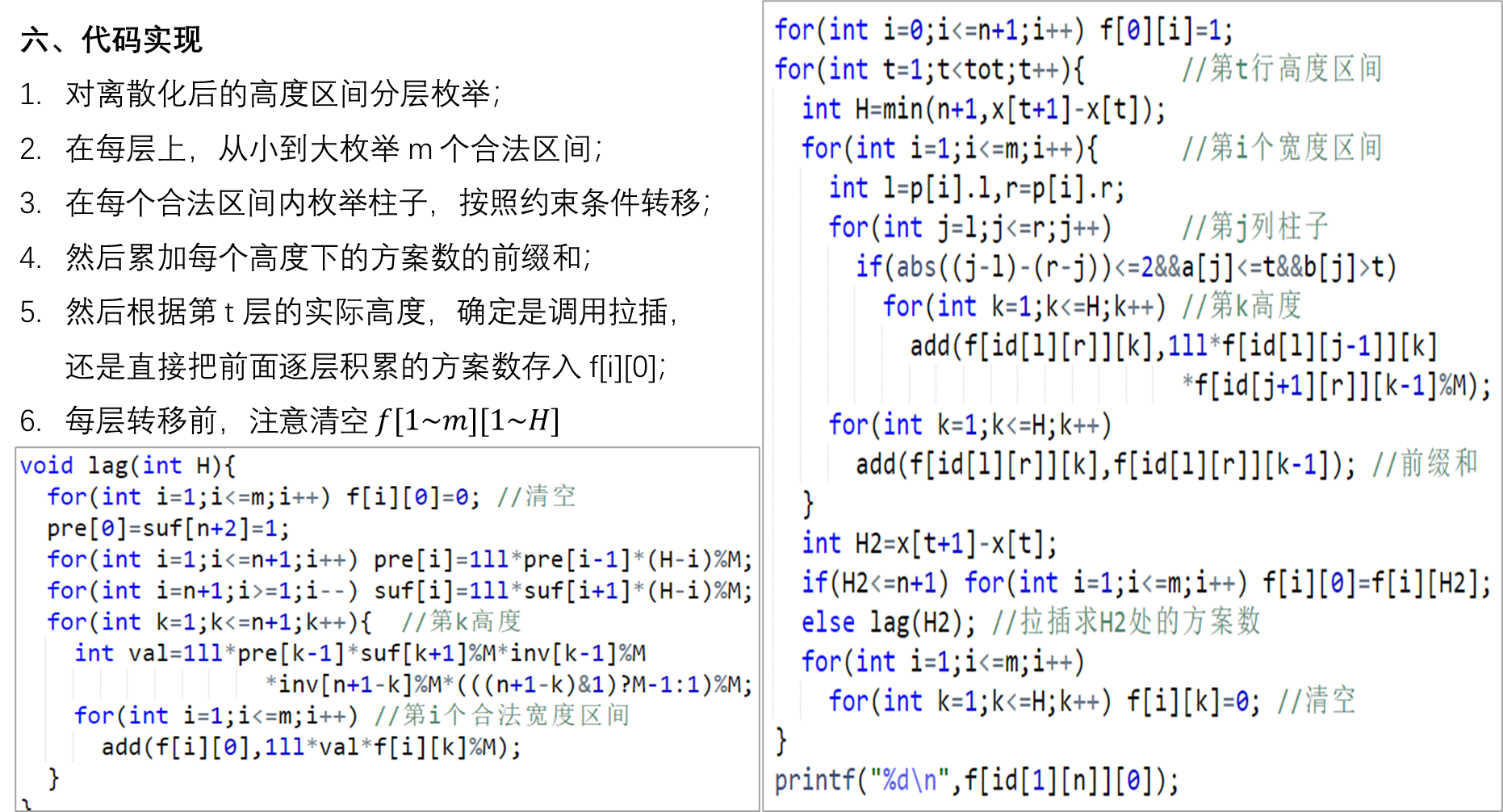
P5469 [NOI2019] 机器人 - 洛谷 | 计算机科学教育新生态

// 区间DP+拉插优化 O(n*n*m)
#include<bits/stdc++.h>
using namespace std;

inline int read(){
  int s=0,f=1; char ch=getchar();
  while(!isdigit(ch)) ch=='-'?-1:1,ch=getchar();
  while(isdigit(ch)) s=s*10+(ch^'0'),ch=getchar();
  return f*s;
}
const int N=605,M=1000000007;
struct node{
  int l,r;
  bool operator<(const node &t)const{return r-l<t.r-t.l;}
}p[3000];
int n,m,tot,id[N][N],a[N],b[N],x[N];
int f[3000][N],fac[N],inv[N],pre[N],suf[N];

int ksm(int a,int b){
  int s=1;
  while(b){
    if(b&1) s=1ll*s*a%M;
    a=1ll*a*a%M;
    b>>=1;
  }
  return s;
}
void dfs(int l,int r){
  if(id[l][r]||l>r) return;
  id[l][r]=++m; 
  p[m]={l,r}; //合法的宽度区间
  for(int i=l;i<=r;i++)
    if(abs((i-l)-(r-i))<=2)
      dfs(l,i-1),dfs(i+1,r);
}
void add(int &a,int b){ //常数优化
  a+=b;
  if(a>=M) a-=M;
}
void lag(int H){
  for(int i=1;i<=m;i++) f[i][0]=0; //清空
  pre[0]=suf[n+2]=1;
  for(int i=1;i<=n+1;i++) pre[i]=1ll*pre[i-1]*(H-i)%M;
  for(int i=n+1;i>=1;i--) suf[i]=1ll*suf[i+1]*(H-i)%M;
  for(int k=1;k<=n+1;k++){  //第k高度
    int val=1ll*pre[k-1]*suf[k+1]%M*inv[k-1]%M*inv[n+1-k]%M*(((n+1-k)&1)?M-1:1)%M;
    for(int i=1;i<=m;i++) //第i个合法宽度区间
      add(f[i][0],1ll*val*f[i][k]%M);
  }
}
int main(){
  n=read();
  fac[0]=inv[0]=1;
  for(int i=1;i<=n;i++) fac[i]=1ll*fac[i-1]*i%M; //阶乘
  inv[n]=ksm(fac[n],M-2);
  for(int i=n-1;i>=1;i--) inv[i]=1ll*inv[i+1]*(i+1)%M; //逆元
  
  dfs(1,n); //搜出所有合法的宽度区间
  sort(p+1,p+m+1); //按宽度升序
  
  for(int i=1;i<=n;i++){
    x[++tot]=a[i]=read();
    x[++tot]=b[i]=read()+1; //高度区间
  }
  sort(x+1,x+tot+1);
  tot=unique(x+1,x+tot+1)-x-1;
  for(int i=1;i<=n;i++){
    a[i]=lower_bound(x+1,x+tot+1,a[i])-x;
    b[i]=lower_bound(x+1,x+tot+1,b[i])-x; //高度区间离散化
  }
  
  for(int i=0;i<=n+1;i++) f[0][i]=1;
  for(int t=1;t<tot;t++){       //第t行高度区间
    int H=min(n+1,x[t+1]-x[t]);
    for(int i=1;i<=m;i++){      //第i个宽度区间
      int l=p[i].l,r=p[i].r;
      for(int j=l;j<=r;j++)     //第j列柱子
        if(abs((j-l)-(r-j))<=2&&a[j]<=t&&b[j]>t)
          for(int k=1;k<=H;k++) //第k高度
            add(f[id[l][r]][k],1ll*f[id[l][j-1]][k]*f[id[j+1][r]][k-1]%M);
      for(int k=1;k<=H;k++) 
        add(f[id[l][r]][k],f[id[l][r]][k-1]); //前缀和
    }
    int H2=x[t+1]-x[t];
    if(H2<=n+1) for(int i=1;i<=m;i++) f[i][0]=f[i][H2];
    else lag(H2); //拉插求H2处的方案数
    for(int i=1;i<=m;i++)
      for(int k=1;k<=H;k++) f[i][k]=0; //清空
  }
  printf("%d\n",f[id[1][n]][0]);
}