[LuoguP3374]树状数组1

链接:https://www.luogu.com.cn/problem/P3374
discription:
已知一个数列，你需要进行下面两种操作：
将某一个数加上 x
求出某区间每一个数的和
input:
1 x k 含义：将第 x 个数加上 k
2 x y 含义：输出区间 [x,y] 内每个数的和
output:
所有2操作的结果.
solution:
引入lowbit运算:例如\(44\ =\ (101100)_2\), 其lowbit即为最低位的\(1\)及其后(可能)的\(0\), 即\((100)_2\)即4.
应该如何计算呢? 考虑简单的位运算:\(lowbit(x)=x\&\sim x+1, 即(101100)_2 \rightarrow(010011)_2\rightarrow (010100)_2\rightarrow (000100)_2\)
也就是\(4\). 在计算机中整数存储的方式就是二进制, 所以根据补码, 取反加一就是取负号. 所以有如下实现:
inline int lowbit(const int& x){return x&-x;}
建立t数组, 初始化为: \(t[x]=\sum_{x-lowbit(x)+1}^{x}arr[x]\)
(图源B站视频截图)

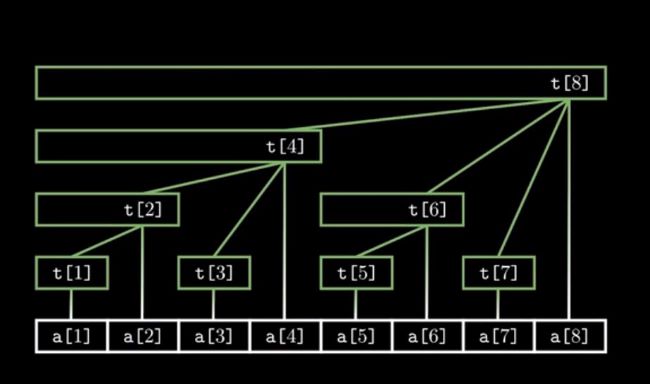
\(Prop1:t[x]节点的段长度为lowbit(x).\)
\(Prop2:t[x]的father为t[x+lowbit(x)]\)
\(Prop3:Treedepth=\lceil{log_2n}\rceil+1\)
\(Prop4:lowbit(lowbit(x))=lowbit(x)\)
代码中实现了:
单点修改
递归寻找下标为\(x以及x+lowbit(x)的所有段和t[i]都要修改\)
区间查询
前缀和\(S=\sum_{x\geqslant t\geqslant 1}t[x] [x\leftarrow x-lowbit(x)]\)
code:

#include<cstdio>
class binarray {
public:
	binarray(int n = 0) :size(n) { arr = new int[n + 1], t = new int[n + 1]; }
	~binarray() { delete[] arr, delete[] t; }
	inline int lowbit(const int& x) const{ return x & -x; }
	void in() {
		for (int i =1 ; i <= size; ++i) {
			t[i] = 0;
			scanf("%d", arr+i);
			for (int j = i - lowbit(i) + 1; j <= i; ++j) t[i] += arr[j];
		}
	}
	inline void add(int x, const int& k) {
		arr[x] += k;
		for (; x <= size; x += lowbit(x))t[x] += k;
	}
	inline int ask(const int& l, const int& r) {
		int ans = 0;
		for (int i = r; i; i -= lowbit(i))ans += t[i];
		for (int i = l - 1; i; i -= lowbit(i))ans -= t[i];
		return ans;
	}
private:
	int* arr;
	int* t;
	int size;
};
int  main() {
	int n, m;
	scanf("%d%d", &n, &m);
	binarray b(n);
	b.in();
	while (m--) {
		int op, x, y;
		scanf("%d%d%d", &op, &x, &y);
		if (op == 1)b.add(x, y);
		else printf("%d\n", b.ask(x, y));
	}
}

binarray是我自己起的名字, 结合了binary和array.