370场leetcode2题题解

100115.找到冠军Ⅰ

​ 一场比赛中共有 n 支队伍，按从 0 到 n - 1 编号。

给你一个下标从 0 开始、大小为 n * n 的二维布尔矩阵 grid 。对于满足 0 <= i, j <= n - 1 且 i != j 的所有 i, j ：如果 grid[i][j] == 1，那么 i 队比 j 队 强 ；否则，j 队比 i 队 强 。

在这场比赛中，如果不存在某支强于 a 队的队伍，则认为 a 队将会是 冠军 。

返回这场比赛中将会成为冠军的队伍。

示例 1：

输入：grid = [[0,1],[0,0]]
输出：0
解释：比赛中有两支队伍。
grid[0][1] == 1 表示 0 队比 1 队强。所以 0 队是冠军。

示例 2：

输入：grid = [[0,0,1],[1,0,1],[0,0,0]]
输出：1
解释：比赛中有三支队伍。
grid[1][0] == 1 表示 1 队比 0 队强。
grid[1][2] == 1 表示 1 队比 2 队强。
所以 1 队是冠军。

​ 读完题目稍微理解一下就是个简单暴力计数体，想明白就简单了。就直接便利寻找谁的1的数量最多即可。

    int findChampion(vector<vector<int>>& grid) {
        int n = grid[0].size();
        
        vector<int> hash(n+1,0);
        
        for(int i=0;i<grid.size();i++)
        {
            for(int j=0;j<n;j++)
            {
                if(grid[i][j]==1)
                {
                    hash[i]++;
                }
            }
        }
        
        int pos=0;
        int num=0;
        for(int i=0;i<hash.size();i++)
        {
            if(num<hash[i])   //几个一
            {
                num=hash[i];
                pos=i;
            }
        }
        
        
        return pos;
    }

100116.找到冠军Ⅱ

​ 一场比赛中共有 n 支队伍，按从 0 到 n - 1 编号。每支队伍也是 有向无环图（DAG） 上的一个节点。

给你一个整数 n 和一个下标从 0 开始、长度为 m 的二维整数数组 edges 表示这个有向无环图，其中 edges[i] = [ui, vi] 表示图中存在一条从 ui 队到 vi 队的有向边。

从 a 队到 b 队的有向边意味着 a 队比 b 队 强 ，也就是 b 队比 a 队 弱 。

在这场比赛中，如果不存在某支强于 a 队的队伍，则认为 a 队将会是 冠军 。

如果这场比赛存在 唯一 一个冠军，则返回将会成为冠军的队伍。否则，返回 -1 。

注意

• 环 是形如 a1, a2, ..., an, an+1 的一个序列，且满足：节点 a1 与节点 an+1 是同一个节点；节点 a1, a2, ..., an 互不相同；对于范围 [1, n] 中的每个 i ，均存在一条从节点 ai 到节点 ai+1 的有向边。
• 有向无环图 是不存在任何环的有向图。

示例 1：

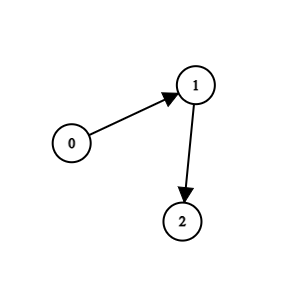
输入：n = 3, edges = [[0,1],[1,2]]
输出：0
解释：1 队比 0 队弱。2 队比 1 队弱。所以冠军是 0 队。

示例 2：

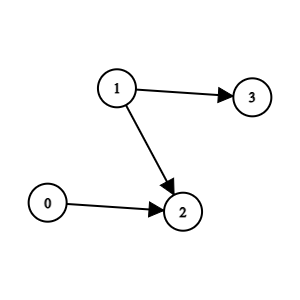
输入：n = 4, edges = [[0,2],[1,3],[1,2]]
输出：-1
解释：2 队比 0 队和 1 队弱。3 队比 1 队弱。但是 1 队和 0 队之间不存在强弱对比。所以答案是 -1 。

​ 对于本题，我们直接寻找入度为0的那个元素，如果有多个入度为0的元素，那么说明有多个队伍无对比，不能确定冠军，返回-1即可，否则返回唯一的入度为0的那个元素即可，本题也是中等题里的简单题，用个hash思想也是简单解决。

    int findChampion(int n, vector<vector<int>>& edges) {
        // 创建入度数组
        vector<int> indegree(n, 0);
        for (auto& edge : edges) {
            int v = edge[1];
            indegree[v]++;
        }

        // 找到入度为0的节点作为冠军
        int winner = -1;
        for (int i = 0; i < n; i++) {
            if (indegree[i] == 0) {
                if (winner != -1) {
                    // 如果存在多个入度为0的节点，则无法确定冠军
                    return -1;
                }
                winner = i;
            }
        }

        return winner;
    }