【数学建模】day14-建立GM(1,1)预测评估模型应用
学习建立GM(1,1)灰色预测评估模型,解决实际问题:
SARS疫情对某些经济指标的影响问题
一、问题的提出
2003 年的 SARS 疫情对中国部分行业的经济发展产生了一定影响,特别是对部分 疫情较严重的省市的相关行业所造成的影响是显著的,经济影响主要分为直接经济影响 和间接影响。直接经济影响涉及商品零售业、旅游业、综合服务等行业。很多方面难以 进行定量的评估,现仅就 SARS 疫情较重的某市商品零售业、旅游业和综合服务业的影 响进行定量的评估分析。
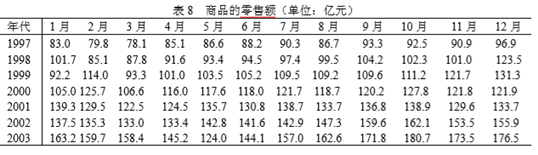
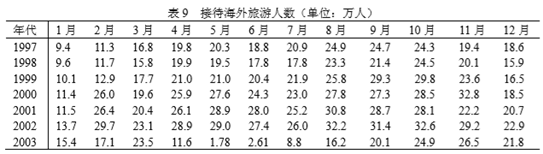
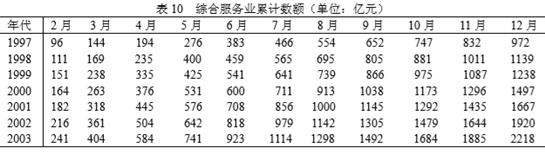
究竟 SARS 疫情对商品零售业、旅游业和综合服务业的影响有多大,已知某市从 1997 年 1 月到 2003 年 12 月的商品零售额、接待旅游人数和综合服务收入的统计数据如下面三表所示。
试根据这些历史数据建立预测评估模型,评估 2003 年 SARS 疫情给该市的商品零 售业、旅游业和综合服务业所造成的影响。
二、模型的分析与假设
模型分析:
根据所掌握的历史统计数据可以看出,在正常情况下,全年的平均值较好地反映了相关指标的变化规律。这样,对于每一个经济指标,考虑从两部分着手建立预测评估模型:
- 利用灰色理论建立GM(1,1)模型,根据1997-2002年的平均值序列,预测2003年的平均值。
- 通过历史数据计算每一个月的指标值与全年总值之间的关系,并将此关系拓展到2003年,进而预测出2003年每一个月的指标值。进而与真实数据值作比较,从而得出结论。
模型假设:
- 假设所有的统计数据真实可靠。
- 假设该市SARS疫情流行期间和结束之后,数据的变化只与SARS疫情的影响有关,不考虑其他随机因素的影响。
三、建立灰色预测模型GM(1,1)
由已知数据,对于1997-2002年的某项指标记为A= (aij)6*12,计算每年的平均值作为初始数列。记为:
式中:
取x(1)的加权均值序列:
式中,α是确定参数。
从而,GM(1,1)的白化微分方程模型为:
其中a是发展灰度,b 是内生控制灰度。
相应的灰微分方程为:
或记为:
这样,我们就得到了微分方程的解。
根据解式,我们可以求出2003年的平均值x拔,从而得到2003年的全年总值Z。
另一方面,根据历史数据,得到第i个月指标值占全年总值的比重为:
此比重拓展到2003年,可以得到2003 年每一个月的指标值V =zu 。
四、模型的求解
对三项指标建立的微分方程模型分别求解如下:
(1)商品零售额
第一指标的数据保存han1.txt,数据如下:
83.0 79.8 78.1 85.1 86.6 88.2 90.3 86.7 93.3 92.5 90.9 96.9 101.7 85.1 87.8 91.6 93.4 94.5 97.4 99.5 104.2 102.3 101.0 123.5 92.2 114.0 93.3 101.0 103.5 105.2 109.5 109.2 109.6 111.2 121.7 131.3 105.0 125.7 106.6 116.0 117.6 118.0 121.7 118.7 120.2 127.8 121.8 121.9 139.3 129.5 122.5 124.5 135.7 130.8 138.7 133.7 136.8 138.9 129.6 133.7 137.5 135.3 133.0 133.4 142.8 141.6 142.9 147.3 159.6 162.1 153.5 155.9 163.2 159.7 158.4 145.2 124.0 144.1 157.0 162.6 171.8 180.7 173.5 176.5
计算的matlab程序如下:1 clc,clear 2 load han1.txt 3 han1(end,:) = []; %删除最后一行,即2003年的值 4 m = size(han1,2); %矩阵列数 5 x0 = mean(han1,2); %矩阵每一行均值 6 x1 = cumsum(x0); %1-AGO序列 7 alpha = 0.4; 8 n = length(x0); 9 z1 = alpha*x1(2:n) +(1-alpha) * x1(1:n-1); %邻值生成值 10 Y = x0(2:n); 11 B = [-z1,ones(n-1,1)]; 12 ab = B\Y %最小二乘拟合参数 13 %下面求年平均值的预测值,取n=6预测下一年度 14 x_hat = (x0(1) - ab(2)/ab(1)) *(exp(-ab(1)*n)-exp(-ab(1)*(n-1))) 15 z = m*x_hat %全年预测值 16 u =sum(han1)/sum(sum(han1)) %根据历史数据计算每个月的比例值 17 v = z*u %计算每个月的预测值
结果:ab =
-0.0993
85.5985
x_hat =162.8793
z =1.9546e+03
u =1 至 6 列
0.0794 0.0807 0.0749 0.0786 0.0819 0.0818
7 至 12 列
0.0845 0.0838 0.0872 0.0886 0.0866 0.0920
v =1 至 6 列
155.2152 157.7365 146.4023 153.5421 160.1400 159.8337
7 至 12 列
165.0649 163.7924 170.5317 173.1473 169.3064 179.8394
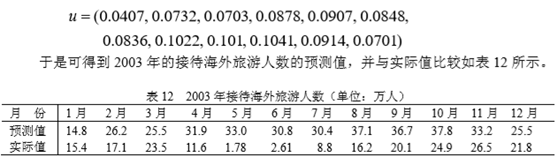
(2)接待海外旅游人数
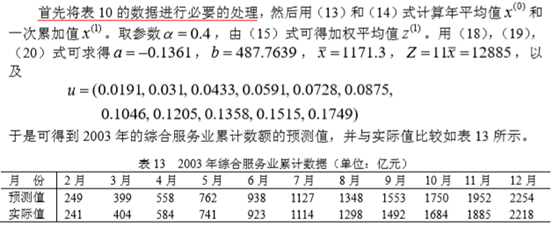
(3)综合服务业累计数据
五、模型的结果与分析
根据该市的统计报告显示,2003 年 4、 5、 6 三个月的实际商品零售额分别为 145.2、 124、144.1 亿元。在这之前,根据统计部门的估计 4、5、6 三个月份 SARS 疫情对该市 的商品零售业的影响为严重,这三个月估计大约损失 62 亿元左右。从我们的模型预 测结果来计算,4、5、6 三个月的损失为 60.1 亿元,这个数基本与专家的估计值相符, 8 月基本恢复正常,这也说明了模型的正确性和可靠性。
对于旅游业来说是受影响严重的行业之一,严重的 4、5、6、7 四个月就损失 100 多万人,按新统计数据,平均每人消费 1002 美元计算,大约损失 10 亿美元。全 年大约损失 162 万人,约合 16.2 亿美元,到年底基本恢复正常。
对于综合服务业中的部分行业影响较大,如航空交通运输、宾馆餐饮等,但有些 行业影响不大,如电信、通讯等,总平均来看,影响还不算太大,5、6、7、8 四个月 大约损失 70 亿元。
该模型虽是就某经济指标的发展规律进行评估预测而建立的,但类似地也适用于 其它方面的一些数据规律的评估预测问题,即该模型具有很广泛的应用性。
不足之处:此处并没有做GM(1,1)的模型检验。



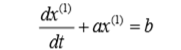

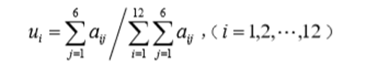



 浙公网安备 33010602011771号
浙公网安备 33010602011771号