【数学建模】day07-数理统计II
方差分析和回归分析。
用数理统计分析试验结果、鉴别各因素对结果影响程度的方法称为方差分析(Analysis Of Variance),记作 ANOVA。
比如:从用不同工艺制作成的灯泡中,各自抽取了若干个测量寿命,腿短这几种工艺制成的灯泡是否有显著差异;用几种化肥和几种小麦品种种子在若干试验田里种植小麦,腿短不同的化肥和小麦品种对产量有无显著影响。
简而言之,就是对影响指标(实验的结果)的诸多因素进行分析,找出有显著影响的因素。不同的因素叫做一个水平。比如,用化肥1、品种1就是因素处于一个水平,达到指标1(产量),用方差分析的方法得到的是某个因素对指标的影响是不是显著的,比如用化肥1还是2这个因素对产量影响是否是显著的。
单因素方差分析 只考虑一个因素 A对所关心的指标的影响, A取几个水平,在每个水平上作若干 个试验,试验过程中除 A外其它影响指标的因素都保持不变(只有随机因素存在),我 们的任务是从试验结果推断,因素 A对指标有无显著影响,即当 A取不同水平时指标 有无显著差别。
方差分析的理论推导(建模写作必备)见《数学建模算法与应用》。
MATLAB实现:
1. 单因素方差分析
1)均衡数据(单因素A的每个水平取样数相同)
p = anoval(x)
param:
x:m*r的矩阵,m是每个水平取样数,r是A因素的水平数。即,x的一列是一个水平的取样数据。
return:
p是一个概率,当p>α(α默认0.05)时接受H0,否则拒绝H0。接受H0说明A因素对于指标没有显著影响,也即没有差异;拒绝H0说明是有显著影响的。
此外,还输出一个方差表和Box图。
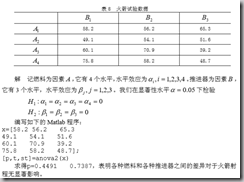
注意:接受H0 ,是将 5 名工人的生产率作为一个整体进行假设检验的结果,并不表 明取其中 2 个工人的生产率作两总体的均值检验时,也一定接受均值相等的假设。
例子:
2) 非均衡数据(单因素的各个水平取样数不同)
p = anoval(x,group);
param:
x :为向量,从第 1 组到第r 组数据依次排列;
group: 为与 x 同长度的向量,标志 x 中数据的组别(在与 x 第i组数据相对应的位置处输入整数 ) 。也就是group向量的每一个数说明x的一个数是属于哪个组。
例子:
2. 双因素方差分析
统计工具箱中用 anova2 作双因素方差分析。命令为
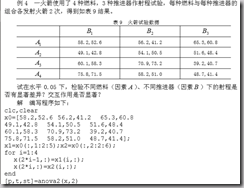
p=anova2(x,reps)
param:
x :不同列的数据表示单一因素的变化情况,不同行中的数据表示另一因素的变化情 况。
如果每种行—列对(“单元”)有不止一个的观测值,则用参数 reps 来表明每个“单 元”多个观测值的不同标号,即 reps 给出重复试验的次数t。
例子:
2. 回归分析
回归分析与曲线拟合区分。
曲线拟合是,根据得到的若干有关变量的一组数据,寻找因变量与(一个或几个)自变量之间的一个函数,使这个函数对那组数据拟合得好。通常,函数的形式可以由经验、先验知识或对数据的直观观察决定,要 作的工作是由数据用小二乘法计算函数中的待定系数。
但是,从数理统计的观点看,这里涉及的都是随机变量,我们根据一个样本计算出的那些系数,只是它们的一个(点)估计,应该对它们作区间估计或假设检验,如果置信区间太大,甚至包含了零点,那么系数的估计值是没有多大意义的。可以用方差分析 方法对模型的误差进行分析,对拟合的优劣给出评价。
简而言之:回归分析就是对拟合问题作的统计分析。
1)必备的知识(重点)
数理统计样本方差,样本均值、期望、方差、k阶矩、k阶中心距的概念。
数据的标准化处理:
2)一元线性回归
1. 用最小二乘法求出回归系数(即回归方程的待定系数)。
2. 拟合效果分析
看以下几个标度:
a. 残差的样本方差(标准差)
拟合方程求出的y与真实的y之差叫残差。求这个残差的方差。越小越精确。
b. 判定系数(拟合优度)
建立一元线性回归模型的目的, 就是试图以x 的线性函数来解释 y 的变异。
->求样本的y的方差,记做SST:
->求回归方程求出的y估的方差,记做SSR:
->SSE = SST - SSR,即为残差平方和:
->可以看到: SSE = SST - SSR; dfT = dfR + dfE;
从上式可以看出,y 的变异是由两方面的原因引起的;一是由于x 的取值不同,而 给 y 带来的系统性变异;另一个是由除 x以外的其它因素的影响。
也就是说:
从而,可以指定判定如下:
定义一个测量标准来说明回归方程对原始数据的拟合程度,这就是所谓 的判定系数,有些文献上也称之为拟合优度。
3. 显著性检验
一元线性回归,我们假设的是y和x是线性关系,但这个线性关系的假定是否靠谱,还要进行显著性检验。
换句话说,β1系数就是线性程度,若β1趋向0,则线性关系不显著。
假设检验:
H0:β1 = 0;
H1:β1 ≠ 0;
传统检验,若接受H0,则线性关系不显著。
4. 回归系数的显著性检验
回归参数的检验是考察每一个自变量对因变量的影响是否显著。换句话说,就是要 检验每一个总体参数是否显著不为零。
也就是说,若某一个回归系数接近0,那么这个对应的变量对y的影响就是不显著的。我们对每一个回归系数进行是否等于0的假设检验,得到显著性分析。
对于每一个βi,检验:
H0:βi = 0;
H1:βi ≠ 0;
决策为:
5. 利用回归方程进行预测
这里有点估计、区间估计。
点预测代数即可。
区间预测比较复杂,用到需要查阅。
===
多元线性回归的步骤与上述类似,回归系数更多,检验统计量不同,用到的时候查阅即可。而且,某些判定标准也有出入,用到需要仔细研读《数学建模算法与应用》。
接下来要继续的:
MATLAB中的多元线性回归:(记忆的)
(多项式的,一次的,二次的。。。)
偏相关系数。
逐次回归(重要)。
岭估计(岭回归)。
主成分估计。










 浙公网安备 33010602011771号
浙公网安备 33010602011771号