逻辑回归简介

　　在学习中我们所涉及到的线性模型因变量往往是连续的。但是实际工作中，人们常常碰到非连续型因变量。然后首先考虑的因变量数据类型是0-1型数据。

　　在日常生活中我们常面临无数的决策，而决策就是一个0-1型的选择问题。如果想要研究、理解并优化我们的选择和决策，就需要构建以0-1型Y为目标的回归 分析模型。

　　Logistic回归虽然名字里带回归，但实际是一种分类算法，主要用于二分类问题，利用了sigmoid函数，即

import numpy as np
from matplotlib import pyplot as plt

x = np.arange(-5,5,0.01)
y = 1/(1+np.exp(-x))

plt.plot(x,y)
plt.xlabel('z')
plt.ylabel('y')
plt.grid()
plt.show()

 

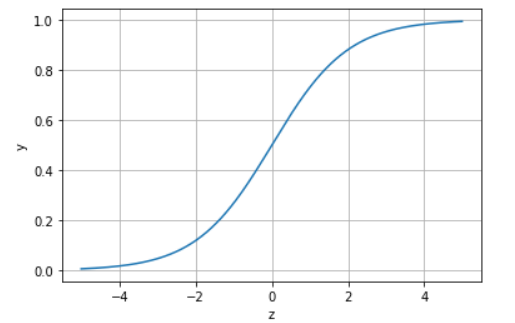
　　sigmoid函数能将线性回归的结果映射到0~1，当结果大于0.5，分类为1，当结果小于0.5，分类为0。其得出的值便可以看做类别1的概率预测值。

　　逻辑回归的优点：1.对分类的可能性进行建模，无需事先假设数据满足某种分布类型；2.不仅可以预测出样本，还可以得到预测为某类别的近似概率。

　　逻辑回归的缺点：线性模型只能做线性分类，不适合处理非线性的情况，一般需要结合较多的人工特征处理使用。

　　时间原因暂时写到此处，后面将继续补充Python逻辑回归实例。