moe笔记
moe(混合专家模型)
作为一种基于 Transformer 架构的模型,混合专家模型主要由两个关键部分组成:
- 稀疏 MoE 层: 这些层代替了传统 Transformer 模型中的前馈网络 (FFN) 层。MoE 层包含若干“专家”(例如 8 个),每个专家本身是一个独立的神经网络。在实际应用中,这些专家通常是前馈网络 (FFN),但它们也可以是更复杂的网络结构,甚至可以是 MoE 层本身,从而形成层级式的 MoE 结构。
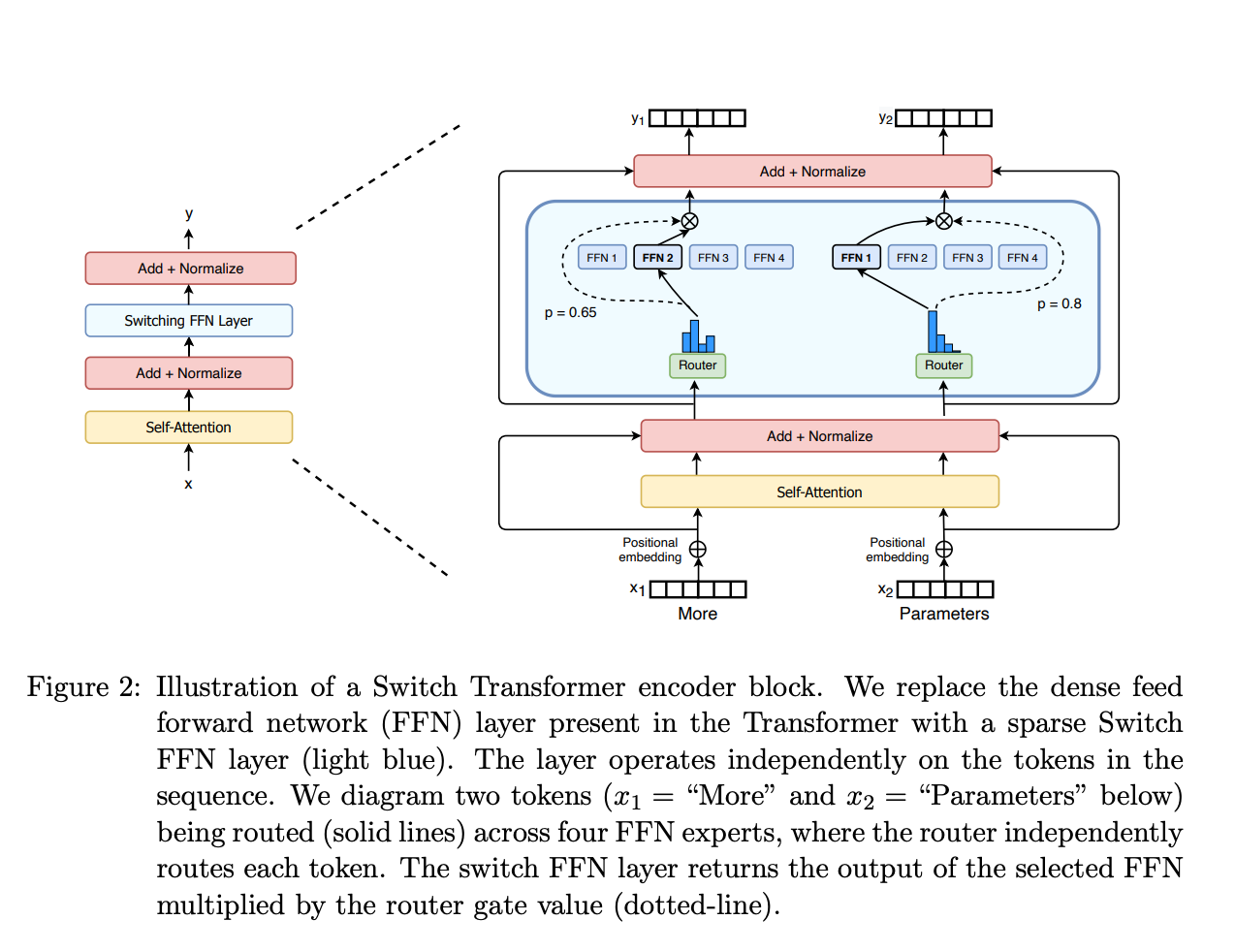
- 门控网络或路由: 这个部分用于决定哪些令牌 (token) 被发送到哪个专家。例如,在下图中,“More”这个令牌可能被发送到第二个专家,而“Parameters”这个令牌被发送到第一个专家。有时,一个令牌甚至可以被发送到多个专家。令牌的路由方式是 MoE 使用中的一个关键点,因为路由器由学习的参数组成,并且与网络的其他部分一同进行预训练。
moe 架构图:
moe参数计算
一、先理清Mixtral 8x7B的参数构成:为什么是47B而非56B?
MoE模型的参数并非“所有部分都独立拆分”,而是“共享基础层 + 独立专家层(FFN) ”的混合结构,这是理解参数总量的关键:
- 核心定义:Mixtral 8x7B的“8x7B”是“8个专家,每个专家的参数规模等效7B稠密模型”,但仅FFN层(前馈神经网络层) 是8个专家独立拥有的,其他层(如注意力层、归一化层、嵌入层)是所有专家共享的。
- 参数计算逻辑:
- 先看7B稠密模型的参数分布:7B参数中,FFN层占比约60%-70%(行业常规比例,以60%为例),即7B×60%≈4.2B/专家;
- 8个专家的独立FFN参数:8×4.2B≈33.6B;
- 共享层参数(非FFN部分):7B - 4.2B≈2.8B(这部分不随专家数量增加而增加);
- 总参数≈33.6B(独立FFN)+ 2.8B(共享层)≈36.4B?——不对,实际Mixtral 8x7B的等效稠密参数是47B,本质是“7B专家的FFN占比更高”(约77%):
7B×77%≈5.39B/专家 → 8×5.39B≈43.1B(独立FFN)+(7B-5.39B)≈3.61B(共享层)≈46.7B,四舍五入为47B。
- 关键结论:MoE的“总参数”不是“专家数×单专家参数”的简单乘积,而是“独立专家层参数 + 共享层参数”,因此Mixtral 8x7B是47B而非56B。
二、推理速度:为什么等效12B稠密模型,而非14B?
MoE推理速度快的核心是“每个令牌只激活部分专家”,Mixtral的规则是“每个令牌激活2个专家”,但需注意“共享层不重复计算”:
- 稠密模型的计算逻辑:推理时,所有层(注意力、FFN、归一化)都要对每个令牌计算,比如12B稠密模型,每个令牌要完成12B参数对应的所有FLOPs(浮点运算次数)。
- MoE的计算逻辑:
- 共享层:注意力、归一化等共享层,对每个令牌只计算1次(和7B稠密模型的共享层计算量一致,因为共享层参数是7B的非FFN部分);
- 专家层(FFN):每个令牌只激活2个专家的FFN层,即计算“2个专家的FFN参数”(而非8个)——2×(7B中的FFN参数≈5.39B)≈10.78B;
- 总计算量等效:共享层(≈3.61B)+ 激活的FFN层(≈10.78B)≈14.39B?——但实际等效12B,原因是“FFN层的计算占比更高,且共享层的计算量可被优化抵消”:
稠密模型中FFN层是计算密集型核心(占总FLOPs的70%以上),MoE的计算量主要由“激活的FFN”决定:2个专家的FFN计算量≈2×(7B稠密模型的FFN FLOPs),而7B稠密模型的FFN FLOPs≈7B×0.7(占比)≈4.9B,2×4.9B≈9.8B;再加上共享层的少量计算(≈7B×0.3≈2.1B),总FLOPs≈11.9B,接近12B,因此说“推理速度类似12B稠密模型”。
- 关键结论:MoE推理速度由“激活的专家数×单专家FFN计算量 + 共享层计算量”决定,而非总参数;Mixtral因“激活2个专家+共享层优化”,计算量等效12B稠密模型,比47B总参数的稠密模型快得多。
三、内存需求:为什么需要容纳47B参数的VRAM?
这是MoE推理的核心挑战——“参数全加载,不管用不用”:
- 内存的作用:推理时,模型的所有参数必须先加载到VRAM(显存)中,才能进行计算(CPU内存速度太慢,无法支撑大模型实时推理);
- MoE的参数加载逻辑:虽然推理时只激活2个专家,但8个专家的所有FFN参数(≈43.1B)+ 共享层参数(≈3.61B)= 47B参数,必须全部加载到VRAM中——因为模型需要“随时选择激活哪2个专家”,无法提前预判并只加载部分专家参数(否则会因“参数缺失”导致推理错误);
- 对比稠密模型:如果是47B的稠密模型,推理时也需要加载47B参数到VRAM;但MoE的优势是“加载47B参数,却只做12B的计算量”,而稠密模型“加载47B参数,要做47B的计算量”——因此MoE在“相同内存占用下,速度更快”,但代价是“内存占用必须达到总参数规模(47B)”。
- 关键结论:MoE的“内存需求”由“总参数(共享层+所有专家层)”决定,而非“激活的参数”,因此Mixtral 8x7B需要能容纳47B参数的VRAM(约需100GB+ VRAM,因参数需存储为FP16/FP8格式,1个FP16参数占2字节,47B×2≈94GB)。
四、总结:MoE推理的“矛盾与平衡”
| 维度 | MoE(Mixtral 8x7B) | 同参数稠密模型(47B) | 同计算量稠密模型(12B) |
|---|---|---|---|
| 参数总量 | 47B(共享层+8个专家FFN) | 47B(全层稠密) | 12B(全层稠密) |
| 推理内存需求 | 高(需加载47B参数) | 高(需加载47B参数) | 低(仅需加载12B参数) |
| 推理计算量(FLOPs) | 低(等效12B) | 高(等效47B) | 低(等效12B) |
| 推理速度 | 快(计算量低) | 慢(计算量高) | 快(计算量低) |
核心结论:MoE通过“参数全加载(高内存)换计算量减少(快速度) ”,解决了“大参数模型推理慢”的问题,但代价是“对VRAM的需求极高”——这也是当前MoE落地的主要瓶颈(需高显存GPU或分布式显存技术)。
moe gate
一、MoE门控的核心逻辑:用“加权选择”减少专家计算
MoE模型的输出是门控网络(G)对多个专家(E)的输出做加权求和,公式是:
- 门控网络(G)的作用:决定“哪些专家参与计算”——如果G(x)的某一项为0,对应的专家就不用计算,从而节省资源。
二、典型门控机制:Softmax+Top-K+噪声
门控网络不是简单的“选专家”,而是通过3步实现“稀疏激活+负载均衡”:
-
基础门控:Softmax网络
门控网络是一个带Softmax的简单网络,学习给不同专家分配权重:\[G_\sigma(x) = \text{Softmax}(x \cdot W_g) \] -
优化门控:带噪声的Top-K门控(Noisy Top-K Gating)
为了更高效地稀疏激活、同时避免专家“忙闲不均”,引入了3步操作:- 加噪声:给门控输出加随机噪声,避免少数专家被过度选择(负载均衡):\[H(x)_i = (x \cdot W_g)_i + \text{StandardNormal}() \cdot \text{Softplus}((x \cdot W_{\text{noise}})_i) \]
- 选Top-K:只保留权重前K个的专家(其他设为-∞,后续Softmax后权重接近0),实现“只激活少数专家”:\[\text{KeepTopK}(v,k)_i = \begin{cases} v_i & \text{if } v_i \text{是} v \text{的前}k\text{个元素} \\ -\infty & \text{否则} \end{cases} \]
- 再Softmax:对Top-K后的结果做Softmax,得到最终专家权重:\[G(x) = \text{Softmax}(\text{KeepTopK}(H(x),k)) \]
- 加噪声:给门控输出加随机噪声,避免少数专家被过度选择(负载均衡):
三、关键特性与作用
- 省计算:选小K值(比如1-2),只激活少数专家,训练/推理速度比激活所有专家快很多;
- 负载均衡:加噪声避免“少数专家被频繁调用、多数闲置”;
- 路由有效性:至少选2个专家,让门控网络学会更合理的“输入-专家”匹配(Switch Transformers验证了这一点)。
简单说:MoE用“门控+Top-K+噪声”,既实现了“少算专家省资源”,又解决了“专家忙闲不均”的问题,是大模型提升性能同时控制成本的核心思路之一。
我把GShard中“辅助损失+负载均衡+推理逻辑”的核心概念整理成了清晰的逻辑清单,方便你快速串联所有要点:
GShard-MoE 中的负载均衡机制
一、负载均衡:“软约束+硬限制+随机化”的组合拳
| 方法 | 核心逻辑 | 作用 | 与辅助损失的关系 |
|---|---|---|---|
| 辅助损失 | 给门控网络加损失项,强制门控给所有专家分配的权重更平均 | 软约束:让门控“倾向”公平分配样本 | 基础约束,避免门控天然偏好少数专家 |
| 随机路由 | 第1专家选Top1,第2专家按权重比例随机选(非固定Top2) | 强化公平:用随机性打破“固定Top2”的倾斜 | 补充辅助损失的“软约束”,增加分配的随机性 |
| 专家容量 | 给每个专家设“最大令牌数阈值”,超容量的令牌溢出/丢弃 | 硬限制:适配静态计算+限制单专家负载 | 从资源上限角度,配合辅助损失实现“软硬均衡” |
二、推理效率:“共享层+部分激活”实现“大参数低资源运行”
- 共享计算:自注意力层是所有专家共用的(参数只加载+计算一次);
- 专家计算:Top-2门控仅激活2个专家的FFN层(47B模型中,2个专家的FFN参数≈10B);
- 最终效果:47B总参数的MoE模型,推理时实际计算量仅等效12B稠密模型(共享层≈2B + 激活专家FFN≈10B)。
三、关键结论
GShard通过“辅助损失(软约束)+ 随机路由(随机化)+ 专家容量(硬限制)”解决了MoE的负载不均问题,同时用“共享层+部分激活”实现了“大参数模型用小资源高效推理”,是MoE落地的核心工程方案之一。
Switch Transformers:解决MoE“稳定性+效率”的升级版方案
它是MoE模型的工程化优化版本,核心是用“单专家路由+混合精度+动态容量”,既提升训练效率,又解决MoE的训练不稳定问题。
一、核心创新:“单专家路由”替代Top-2,大幅降本提效
- 对比GShard的Top-2路由:GShard选2个专家,而Switch Transformers只选1个专家(“Switch”即“二选一”的开关逻辑)。
- 带来的优势:
- 降计算负担:门控网络只需选1个专家,计算量比Top-2少一半;
- 减通信成本:激活的专家数从2个变1个,多设备间传输的张量数据量减少;
- 提批量效率:每个专家的令牌批量至少能翻倍(因为1个专家承接更多样本),计算硬件的利用率更高。
- 关键前提:单专家路由没有降低模型质量——这是Switch Transformers最核心的突破(之前普遍认为“至少选2个专家才能保证性能”)。
二、负载均衡:简化辅助损失+动态专家容量
- 简化辅助损失:
不再用复杂的约束项,而是给每个Switch层加一个“轻量辅助损失”,直接鼓励门控把样本均匀分配给所有专家(超参数可调权重),既实现负载均衡,又避免损失函数过于复杂导致训练不稳定。 - 动态专家容量:
容量公式为专家容量 = (每批次令牌数/专家数) × 容量因子,且容量因子可以动态调整(根据训练/推理的计算资源灵活变):- 低容量因子(1~1.25):减少设备间通信成本,适配小资源场景;
- 动态调整:训练时根据计算负载调大/调小,平衡效率与稳定性。
三、混合精度训练:平衡“速度”与“稳定性”
- 矛盾点:用低精度(如bfloat16)能减内存/通信成本,但门控的Softmax等操作对精度敏感,容易训练崩溃。
- 解决方案:“专家用低精度,路由用全精度”:
- 专家的FFN层用bfloat16训练(降成本);
- 门控的路由计算用全精度(保证Softmax等操作的稳定性)。
- 效果:既实现了训练加速,又避免了低精度导致的不稳定,且模型质量没有下降。
四、价值总结
Switch Transformers是MoE落地的关键里程碑:
- 用“单专家路由”打破了“多专家才能保性能”的认知,大幅降低MoE的训练/推理成本;
- 用“简化辅助损失+混合精度”解决了MoE的训练不稳定问题;
- 最终实现“1.6万亿参数模型用更低资源训练/运行”,推动大模型向“大参数+高效能”方向发展。
专家的数量对预训练有何影响?
增加更多专家可以提升处理样本的效率和加速模型的运算速度,但这些优势随着专家数量的增加而递减 (尤其是当专家数量达到 256 或 512 之后更为明显)。同时,这也意味着在推理过程中,需要更多的显存来加载整个模型。值得注意的是,Switch Transformers 的研究表明,其在大规模模型中的特性在小规模模型下也同样适用,即便是每层仅包含 2、4 或 8 个专家。
MoE模型微调
一、核心结论:MoE微调的“特殊性”(对比稠密模型)
1. 过拟合:稀疏模型更“娇气”,正则化要更狠
- 稠密模型过拟合可通过常规dropout、权重衰减解决;
- MoE模型因“专家层稀疏激活”,数据分布更集中(少数专家承接大量样本),更容易过拟合→需针对性优化:
✅ 给稀疏层(专家FFN层)设更高的dropout率(稠密层用低dropout);
✅ 令牌丢弃(训练中主动丢部分令牌)也是一种正则化,即使丢11%令牌,模型性能也不会明显下降。
2. 辅助损失:不是“可有可无”,而是“场景化使用”
- ST-MoE作者发现:预训练/简单微调时关辅助损失影响小(令牌丢弃可替代其正则化作用);
- 指令微调时:开辅助损失能有效防止过拟合,且MoE从辅助损失中获益比稠密模型更多。
3. 任务适配:MoE“挑任务、挑数据量”
- 小任务/小数据集:MoE过拟合严重,验证集表现远差于稠密模型;
- 大任务/大数据集:MoE优势拉满(尤其是知识密集型任务如TriviaQA);
- 任务类型:重理解任务(如SuperGLUE)稠密模型更稳,知识型任务MoE更优。
二、实操策略:MoE微调的“避坑指南”
1. 参数冻结:别冻非专家层,冻MoE层更划算
- 错误做法:冻结非专家层(注意力/嵌入层)→MoE层占模型参数90%以上,仅训专家层会导致性能暴跌;
- 正确做法:冻结MoE层(专家FFN层),只训非专家层→效果几乎和全参数微调一致,且:
✅ 显存需求降一半(不用更新海量专家参数);
✅ 训练速度大幅提升(计算量仅集中在共享层)。
2. 超参数:和稠密模型“反着来”
| 维度 | 稠密模型 | MoE模型 |
|---|---|---|
| 批量大小 | 偏大(如64/128) | 偏小(如16/32) |
| 学习率 | 偏低(如1e-5) | 偏高(如5e-5) |
| → 核心逻辑:MoE专家层激活稀疏,小批量+高学习率能让梯度更新更“聚焦”,避免专家层参数更新过慢/过稳。 |
3. 指令微调:MoE的“性能放大器”(关键突破)
- 普通微调:MoE性能不如同量级稠密模型(如T5);
- 指令微调(尤其是多任务指令微调):
✅ Flan-MoE(MoE的指令微调版本)性能远超原始MoE;
✅ MoE从指令微调中获益的幅度,比Flan-T5(稠密指令微调)远超原始T5的幅度更大→指令微调是MoE发挥优势的关键。
三、场景选择:稀疏VS稠密,怎么选?
| 维度 | MoE模型(稀疏) | 稠密模型 |
|---|---|---|
| 硬件条件 | 多机器、高显存、高吞吐量需求 | 单卡/低显存、低吞吐量 |
| 计算资源 | 固定预训练算力下,效果更优 | 微调算力有限时更易落地 |
| 任务规模 | 大任务、大数据集、知识密集型 | 小任务、小数据集、重理解 |
| 参数量对比 | 无意义(计算逻辑不同) | 参数量可直接对标性能 |
四、总结:MoE微调的核心逻辑
MoE不是“稠密模型的简单扩容版”,而是“针对性适配的稀疏架构”:
- 微调时要抓住「强正则化+冻专家层+小批量高学习率+指令微调」四个关键点;
- 辅助损失要“按需开关”(小任务关、指令微调开);
- 场景上“扬长避短”:大算力、大任务、知识型场景用MoE,小算力、小任务、理解型场景用稠密模型。
moe 高效落地
一、核心痛点:MoE为啥“先天低效”?
原始MoE的分支结构(多专家独立计算)和GPU架构不匹配:
- 硬件适配差:GPU擅长规整的批量计算,但MoE令牌分配不均(专家间令牌数差异大),导致算力利用率低;
- 通信瓶颈:令牌需跨节点传输到对应专家,网络带宽成为性能天花板;
- 显存浪费:所有专家参数都要加载,且激活值存储需求随容量因子升高而暴涨。
二、第一步:并行计算——选对“专家并行”,打牢效率基础
MoE的效率提升,核心是“把专家和数据放到合适的节点上”,先理清四种并行的差异:
| 并行类型 | 核心逻辑 | 适配场景 | MoE关键价值 |
|---|---|---|---|
| 数据并行 | 权重全复制,数据拆分成批次 | 小模型/单专家 | 无(MoE用数据并行会浪费显存) |
| 模型并行 | 模型拆层,数据全复制 | 超大单模型(如千亿稠密) | 无(MoE层内专家拆分不适用) |
| 模型+数据并行 | 层拆到节点,数据拆批次 | 超大规模稠密模型 | 适配性差(专家层无法拆层) |
| 专家并行 | 专家分节点,数据拆批次 | MoE专属(核心!) | 1. 每个节点只存部分专家参数; 2. 令牌只传给对应专家节点,减少通信 |
✅ MoE最优并行策略:专家并行+数据并行结合
- 非MoE层(注意力/嵌入):用数据并行(和稠密模型一致);
- MoE层(专家FFN):用专家并行(每个节点放1个专家,数据拆批次分给节点);
- 效果:既避免专家参数重复存储,又减少跨节点令牌传输量。
三、第二步:成本平衡——容量因子(CF)是“效率调节阀”
容量因子(专家能处理的最大令牌数/理论平均令牌数)是MoE性能与成本的核心权衡点:
- 容量因子越高:
✅ 优点:令牌丢弃少,模型性能好(ST-MoE验证丢11%令牌不影响,但更高丢弃会降效);
❌ 缺点:显存占用暴增(要存更多激活值)、跨节点通信量上升(更多令牌需传输); - 容量因子越低:
✅ 优点:通信/显存成本低,适配带宽有限的硬件;
❌ 缺点:令牌丢弃多,性能可能下降; - 实操初始配置:Top-2路由 + CF=1.25 + 单节点1个专家
- 先按这个基线跑,再根据“通信延迟/显存占用/模型性能”三角平衡调整:
- 带宽够、显存足→调升CF(如1.5);
- 带宽窄、显存紧→调降CF(如1.0)。
- 先按这个基线跑,再根据“通信延迟/显存占用/模型性能”三角平衡调整:
四、第三步:部署提速——把大MoE“变小”,适配落地场景
针对MoE参数规模大、部署难的问题,三种核心技术直接降低落地成本:
| 部署技术 | 核心逻辑 | 效果 | 适用场景 |
|---|---|---|---|
| 预先蒸馏 | 把MoE知识蒸馏到同架构稠密模型 | 保留30-40%稀疏性增益,模型体积大幅缩小 | 本地部署/低显存场景 |
| 任务级别路由 | 路由器直接把整句/任务分给1个专家 | 提取“子网络”(仅保留任务相关专家),简化结构 | 单任务推理(如专属问答) |
| 专家网络聚合 | 合并多个专家的权重 | 推理参数量减少,无需加载所有专家 | 通用推理/吞吐量要求高的场景 |
✅ 实操优先级:预先蒸馏 > 专家聚合 > 任务路由(蒸馏性价比最高,适配绝大多数场景)。
五、第四步:训练加速——从“硬件适配”到“算法重构”
两大核心方案解决MoE训练的“动态性”和“低效计算”问题:
1. FasterMoE(系统级优化):榨干硬件性能
- 核心创新:
① 细粒度通信调度:让令牌传输和计算重叠(边算边传,不浪费时间);
② 拓扑感知门控:根据节点间网络延迟选专家(优先选延迟低的节点的专家); - 效果:训练速度提升17倍(从“硬件等数据”变成“数据追硬件”)。
2. Megablocks(算法级重构):适配GPU的稀疏计算
- 核心痛点:传统MoE用批量矩阵乘法,要求所有专家处理的令牌数相同,令牌分配不均时算力浪费严重;
- 解决方案:把MoE层重构为“块稀疏矩阵乘”:
✅ 不丢弃任何令牌,按令牌实际分布拆成“块”,每个块分配给对应专家;
✅ 适配GPU的块稀疏计算架构,即使专家间令牌数差异大,也能高效计算; - 效果:彻底解决令牌分配不均的低效问题,稀疏预训练效率大幅提升。
六、总结:让MoE“起飞”的核心逻辑
MoE的效率提升不是“单点优化”,而是“并行架构打底 + 容量因子平衡成本 + 部署技术降规模 + 训练技术适配硬件”的组合拳:
- 基础层:用专家并行+数据并行,解决通信和显存的先天瓶颈;
- 平衡层:调优容量因子,在性能和成本间找最优解;
- 落地层:用蒸馏/聚合缩小模型,适配实际部署场景;
- 加速层:用FasterMoE/Megablocks解决训练的硬件适配问题。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号