动态求连续区间和 树状数组 线段树 java

🌹 参考链接

树状数组

⭐ 图解（奇数存本身，偶数存 lowbit 个数的前缀和）

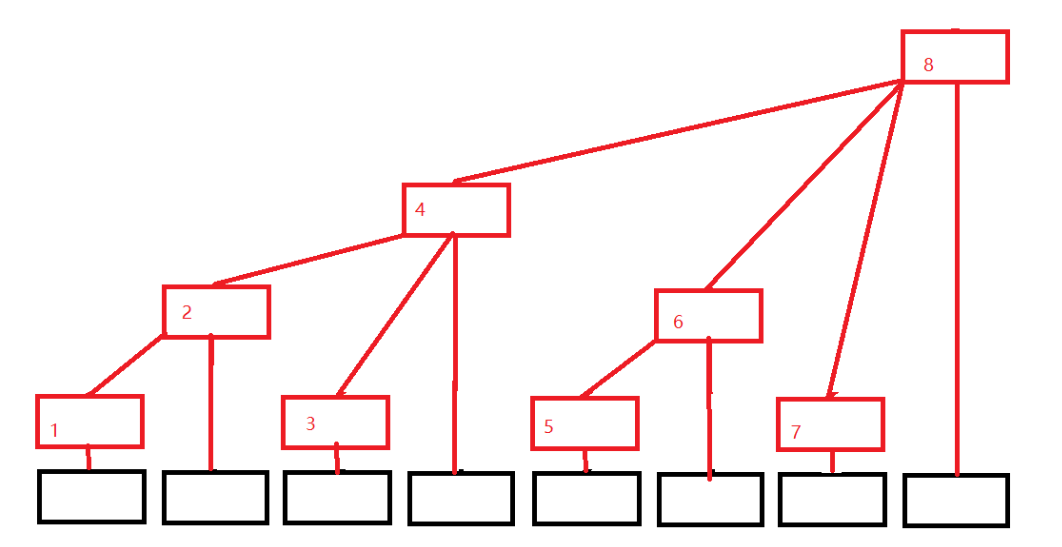
⭐ 支持动态 修改的前缀和
⭐ O（log n）
⭐ 支持的操作：

① 单点修改：在某个位置上加一个数
② 区间查询 ：求某一个前缀和

⭐ 树状数组 本树

static int lowbit(int x)
	{
		return x & -x;
	}

	/* 在 x 的位置上加上 v */
	static void add(int x, int v)
	{
		for (int i = x; i <= n; i += lowbit(i))
			tr[i] += v;
	}

//	查询 x 位置的前缀和
	static int query(int x)
	{
		int res = 0;
		for (int i = x; i != 0; i -= lowbit(i))
		{
			res += tr[i];
		}
		return res;
	}

🤠 例题：动态求连续区间和

10 5
1 2 3 4 5 6 7 8 9 10
1 1 5
0 1 3
0 4 8
1 7 5
0 4 8

输出案例

11
30
35

import java.io.*;

public class Main
{
	static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
	static BufferedWriter out = new BufferedWriter(new OutputStreamWriter(System.out));

	static int N = 100010, n;
	static int[] a = new int[N];
	static int[] tr = new int[N];

	static int lowbit(int x)
	{
		return x & -x;
	}

	/* 在 x 的位置上加上 v */
	static void add(int x, int v)
	{
		for (int i = x; i <= n; i += lowbit(i))
			tr[i] += v;
	}

//	查询 x 位置的前缀和
	static int query(int x)
	{
		int res = 0;
		for (int i = x; i != 0; i -= lowbit(i))
		{
			res += tr[i];
		}
		return res;
	}

	public static void main(String[] args) throws IOException
	{
		String[] ss = in.readLine().split(" ");
		n = Integer.parseInt(ss[0]);
		int m = Integer.parseInt(ss[1]);

		ss = in.readLine().split(" ");
		for (int i = 1; i <= n; i++)
		{
			a[i] = Integer.valueOf((ss[i - 1]));
			add(i, a[i]);
		}

		while (m-- != 0)
		{
			String[] sss = in.readLine().split(" ");
			int k = Integer.parseInt(sss[0]);
			int x = Integer.parseInt(sss[1]);
			int y = Integer.parseInt(sss[2]);
			if (k == 0)
				System.out.println(query(y) - query(x - 1));
			else
			{
				add(x, y);
			}
		}
//		for (int i = 1; i <= n; i++)
//			System.out.print(tr[i] + " ");
	}
}

线段树

⭐ 核心操作

🌹 pushup：用子节点信息更新当前节点信息
🌹 build：在一段区间上初始化线段树
🌹 modify：修改
🌹 query：查询 

⭐ O(log n)

import java.io.*;
import java.util.*;

public class Main
{
	static int N = 100010;
	static int[] w = new int[N];
	static Node[] tr = new Node[N * 4];

	static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
	static BufferedWriter out = new BufferedWriter(new OutputStreamWriter(System.out));

	static class Node
	{
		int l, r;
		int sum;

		public Node(int l, int r, int sum)
		{
			this.l = l;
			this.r = r;
			this.sum = sum;
		}
	}

//	用子节点的sum值更新父节点的sum值
	static void pushup(int u)
	{
		tr[u].sum = tr[u * 2].sum + tr[u * 2 + 1].sum;
	}

	static void build(int u, int l, int r)
	{
		if (l == r)// 叶子节点，sum 值就是本身
		{
			tr[u] = new Node(l, r, w[r]);
		} else
		{
			tr[u] = new Node(l, r, 0);// 非叶子节点的 sum 值在 pushup 上计算
			int mid = l + r >> 1;
			build(u << 1, l, mid);
			build(u << 1 | 1, mid + 1, r);// 细节 | 1 ：相当于先 * 2 再 +1，注意运算符优先级
			pushup(u);// 前边递归完所有节点的边界，后边从下往上计算节点的 sum 值
		}
	}

	static int query(int u, int l, int r)
	{
		if (tr[u].l >= l && tr[u].r <= r)// 求解的区间 包含 当前区间
			return tr[u].sum;

		int mid = tr[u].l + tr[u].r >> 1;
		int sum = 0;
//		递归求 sum
		if (l <= mid)// 递归左儿子
			sum += query(u << 1, l, r);
		if (r > mid)// 递归右儿子
			sum += query(u << 1 | 1, l, r);
		return sum;
	}

	static void modify(int u, int x, int v)
	{
		if (tr[u].l == tr[u].r)
			tr[u].sum += v;
		else
		{
			int mid = tr[u].l + tr[u].r >> 1;
//			直接二分找到要修改的叶子节点
			if (x <= mid)
				modify(u << 1, x, v);
			else
				modify(u << 1 | 1, x, v);
//			记得子节点有改动的区间都要重新 pushup 修改 sum 值
			pushup(u);
		}

	}

	public static void main(String[] args) throws IOException
	{
		String[] ss = in.readLine().split(" ");
		int n = Integer.parseInt(ss[0]);
		int m = Integer.parseInt(ss[1]);
		ss = in.readLine().split(" ");
		for (int i = 1; i <= n; i++)
		{
			w[i] = Integer.parseInt(ss[i - 1]);
		}

//		初始化线段树
		build(1, 1, n);

		while (m-- > 0)
		{
			ss = in.readLine().split(" ");
			int k = Integer.parseInt(ss[0]);
			int a = Integer.parseInt(ss[1]);
			int b = Integer.parseInt(ss[2]);
			if (k == 0)
				System.out.println(query(1, a, b));
			else
			{
				modify(1, a, b);
			}
|  |  |
|--|--|
|  |  |

		}
	}
}

⭐ 本题：线段树比树状数组要慢 1/3 没必要