PID算法理解

在整个控制系统中，pid算法的作用就是稳准快地到达我们需要的目标值，我们通过举例，对一个简单的温度控制系统来定量分析

位式控制算法

在介绍pid控制算法之前，我们先来看一下最简单的位式控制算法

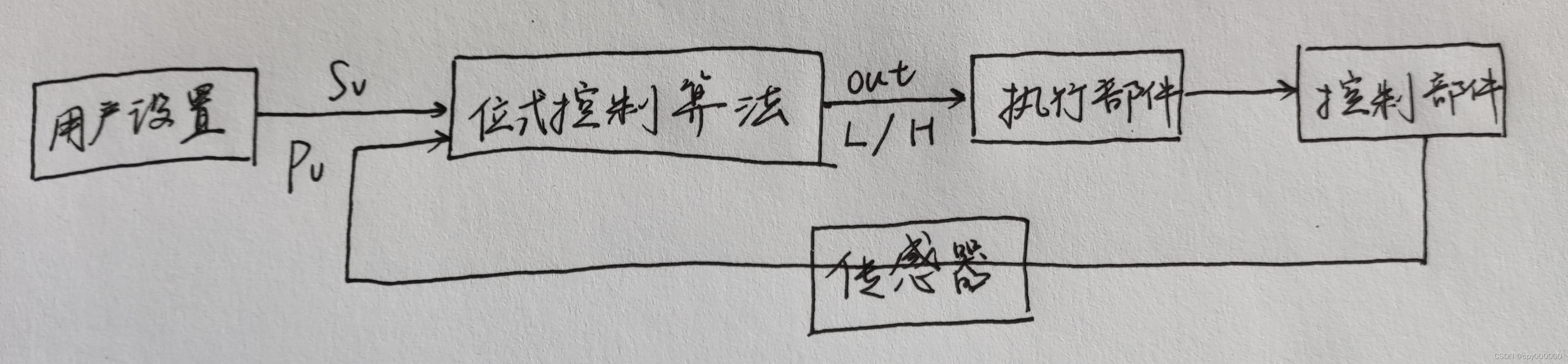
位式控制算法特点：
只能输出低电平和高电平，即开和关两种状态

在温度控制系统中，如果我的目标温度值设置的是100°c，而通过温度传感器得到的当前温度是70°c，那么我的开关闭合，进行加热；反之，温度超过100°c，开关断开或者启动其他制冷装置，进行降温。

这样的一个带有反馈装置的温度控制系统其实已经能满足我们的需求了，但是它存在这几个问题：

1. 加热元件具有惯性作用，即使在我温度到达了100°c停止加热，由于惯性的作用，温度其实还会上升，这就造成了温度的波动
2. 加热的速度由加热元件决定，我们只能控制开关的通断，所以加热的速度是不会变化的。而我们更希望是一个灵活，平滑的控制，比如温度偏差大的时候加热更快，偏差小的时候加热减慢
3. 在考虑有外部干扰时（浇一盆冷水），系统不能进行及时的反馈

pid控制算法

pid算法的提出就是为了解决上面这些问题

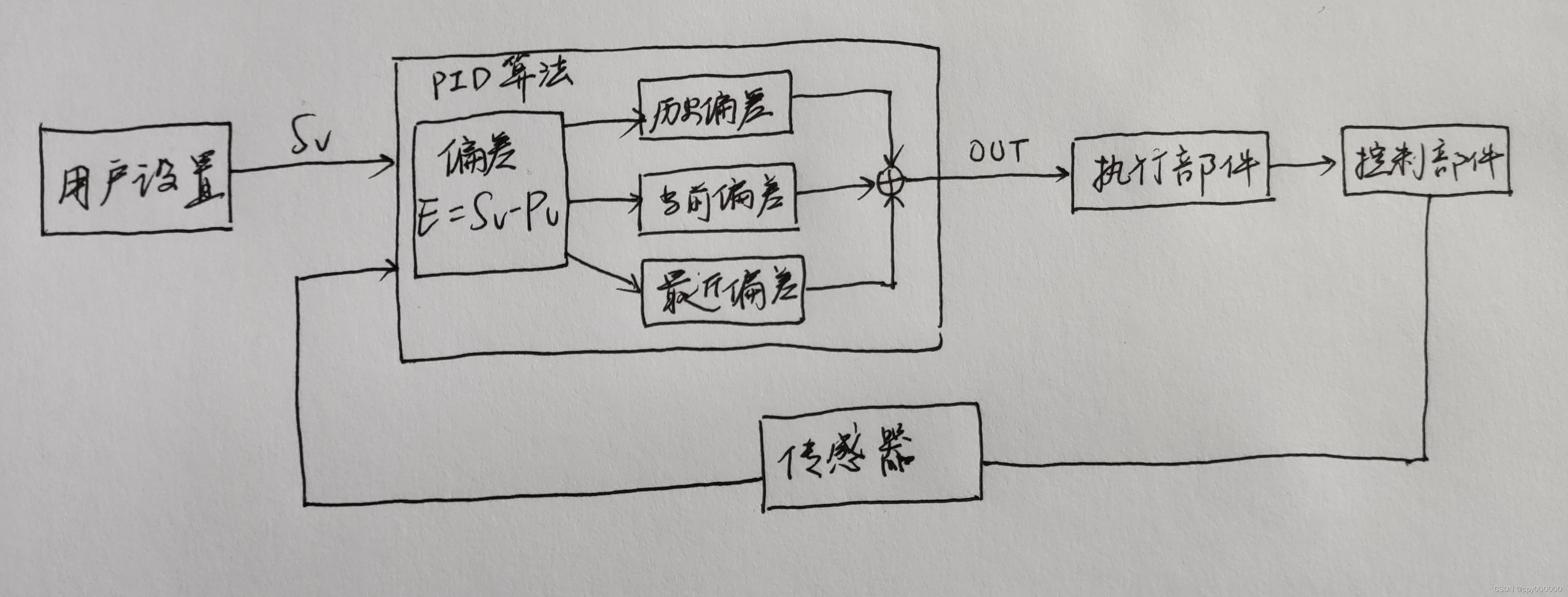
首先，为了解决输出不平滑的问题，我们通常采用pwm输出（本质就是不断地通断开关），相当于现在我们可以控制输出的大小，加热的大小现在是可以变化的。

之后的pid算法得出的结果就是去改变pwm输出的值。我们把比例部分，积分部分，微分部分计算的结果线性叠加，把最后的结果作输出

比例控制部分

我们要把期望值Sv与实际值Pv的差值用起来，记误差e(k) = Pv-Sv，整个pid算法就是在误差e(k)上做文章。

比例部分利用Kp*e(k)作为输入，这样就能让我们的输出随输入线性变化。温度偏差越大，输出的值就越大，加热速度就更快；反之越慢。

这样我们的偏差在刚出现或变化的瞬间，系统会根据偏差量作出及时反应，输出更加平滑，误差减小的速度更快，但在到达期望值，e(k)=0的情况下，输出=0，系统会失去控制作用，并且还会出现超调或者振荡，以及不能消除静态误差的问题。

积分控制部分

积分的存在主要是为了消除静态误差。下面是对静态误差的一个形象解释。
假设现在要往杯里加100ml水，只考虑比例项的作用，在加到80ml的时候，比例部分的计算结果Kp*e(k)使得下次加10ml的水，我们正在离目标值越来越近。但是杯口下刚好有一个缺口，每次漏10ml的水，刚好抵消，我们将永远不会到达目标值。

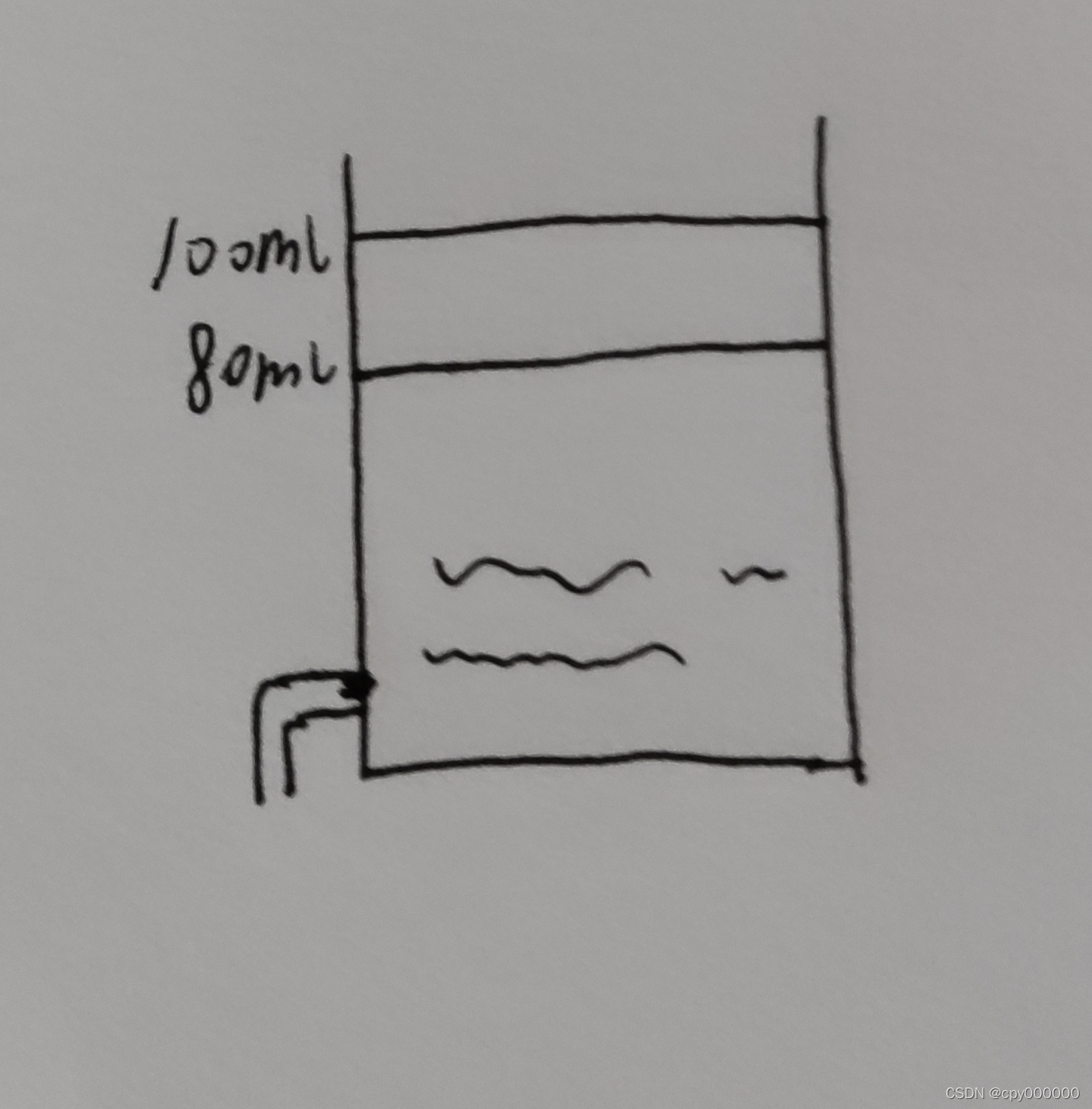
杯子的缺口可以视为系统的干扰。在只有比例部分作用的情况下，我们无法消除静态误差。所以我们加入积分部分Ki *Σe(i)，对过去的误差进行一个累计。换句话说，只要有偏差，积分部分就会起作用。在上面的注水系统中，即使比例项抵消了，因为还有偏差存在，积分项就会不断起作用，系统存在的静态误差随之消除。

同时，因为积分项对过去误差的累计，偏差为0或者很小的时候，比例项会失去对系统的控制，这时就要靠积分项维持输出。(大误差靠比例部分，小误差靠积分部分)

但是，由于积分项是所有误差累积的原因，系统在第一次到达期望值的时候，会有一个很大的误差累积，这会产生一个很大的超调甚至振荡，所以在实际应用中，我每次会在误差累积很大的时候减弱甚至消除积分项的作用。

这样，我们的系统功能又进一步完善。有偏差能快速响应，有静态误差能及时弥补。

微分控制部分

我们的温度控制系统已经有了比例和积分部分来控制。假设现在我们有以下两种情况：一是正常加热，从70°c加热到100°c；二是我们浇了一盆冷水后，在温度骤降的时候将温度从70°c加热到100°c。在只有比例项和积分项的作用时，因为我们只关注当前误差Kp*e(k)和历史累计误差Ki *Σe(i)，无法对温度下降的速度进行反馈，所以从70°c加热到100°c的调节时间显然是后者更长，这不是我们所期望的结果。我们希望的是系统能及时对外界的干扰做出调节，而微分部分刚好就能满足这一需要。

微分Kd *(e(k)-e(k-1))，又可写作Td *((e(k)-e(k-1))/T)，将最近两次的误差作差，再除以采样周期T，就得到了上面提到的一个量–速度。有了温度下降的速度，我们就可以通过这个速度量对系统的输出再进行一次调节。系统检测到温度突然下降，即温度下降速度过快，他不会像原来那样不作为，而是增大输出，提高加热速度；在系统加热速度过快，马上就要超过100°c的时候，他又会减小输出，防止超调。

所以，微分部分能根据偏差量的变化趋势(速度)提前给出较大的控制作用，将偏差消灭在萌芽阶段，这样可以大大减小系统的动态偏差和调节时间，减小超调，克服振荡，使系统的动态调节品质得以改善。

但是，微分作用一个很大的缺陷是容易引入高频噪声，高频率的干扰让微分的输出持续增大，干扰信号严重的情况下微分部分的作用适得其反。

最后，pid控制能大大简化控制系统的设计。因为在调节温度的过程中，从调节温度的旋钮到温度变化，这中间是很复杂的过程，包含动力学还有热力学等等。引入pid就不需要建立这个复杂的数学模型。