迪杰特斯拉算法

一. 迪杰特斯拉算法

迪杰斯特拉算法的基本思路

迪杰斯特拉算法的基本思路:

找出最便宜的顶点，即距离出发顶点距离最近的顶点，作为新的出发顶点
更新该顶点的邻居的开销
重复（1）（2）步骤，直到对每个顶点都做了此操作
计算最终路径

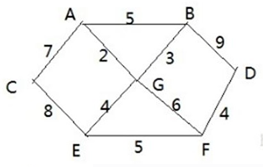
如何对下面的图使用迪杰斯特拉算法

每条边上标识的数字都表示，两个顶点之间的距离。

二. 算法详解

假设要求从 A 到 D 的最短路径,步骤如下：

准备工作：

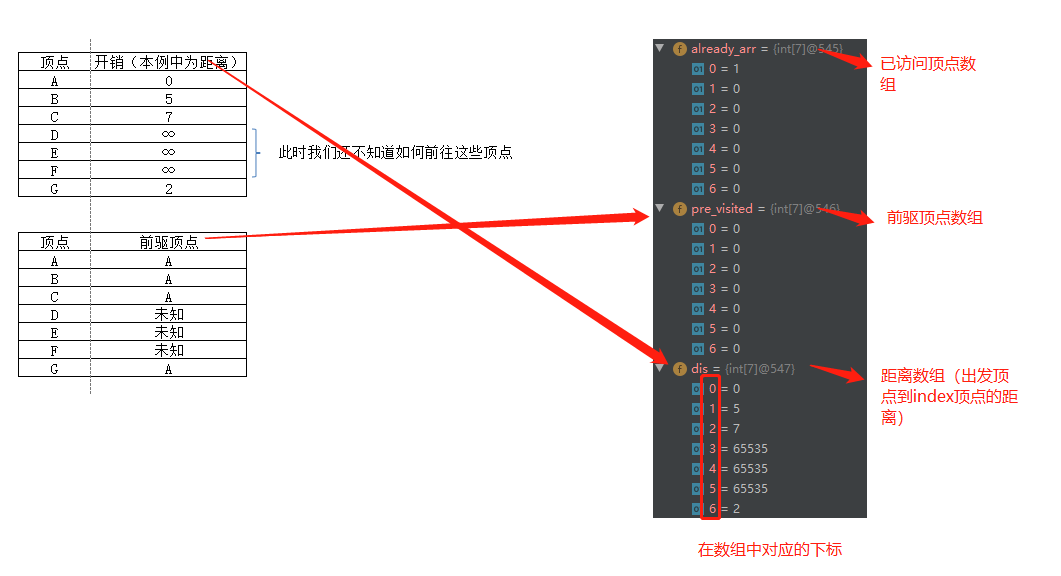
在计算前，需要做一些准备工作，列出每个节点的开销：
在执行迪杰斯特拉算法的过程中，将不断的更新这个表。为了计算最终路径，还需要在表中添加表示父顶点（前驱顶点）的列

第一步：找出最便宜的顶点，作为新的出发顶点（红色标识表示该顶点已经被访问过，选择新的出发顶点是不再考虑该顶点）
站在出发顶点A，与A直连的顶点有：

C(A到C的距离为7)
B(A到B的距离为5)
G(A到G的距离为2)

显然，A到G的距离最近，则G为最便宜的顶点。
此时，由于你还不知道从A出发到其它非直连的顶点的距离是多少，因此，我们都将他们暂时设为无穷大

第二步：更新顶点G的邻居的开销

计算从出发顶点A出发，经过G顶点，到G的各个邻居（与G直连的顶点）的开销

G顶点的邻居有：

顶点A（A被访问过）
顶点B（G到B的距离为3）
顶点E（G到E的距离为4）
顶点F（G到F的距离为6）

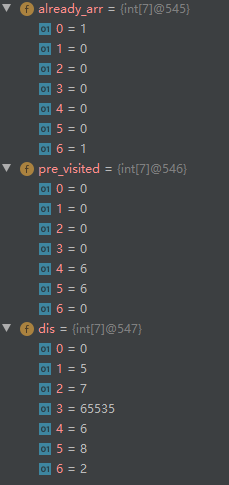
再执行
第一步：下一个最便宜的顶点是B

第二步：更新顶点B的邻居的开销
B顶点的邻居有：
- 顶点A （A被访问过）
- 顶点G（G被访问过）
- 顶点D （B到D的距离为9）

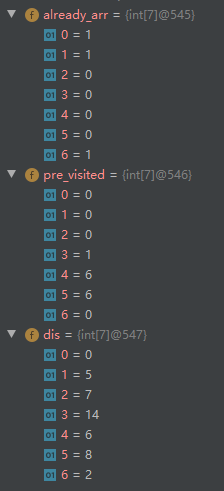
再执行
第一步：下一个最便宜的顶点是E

第二步：更新顶点E的邻居的开销
E顶点的邻居有：
- 顶点C（E到C的距离为8）
- 顶点G（G被访问过）
- 顶点F （E到F的距离为5）

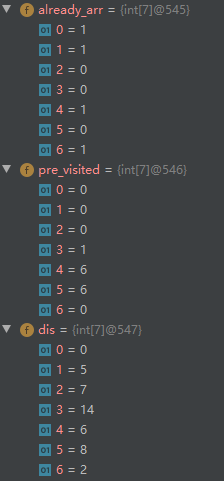
再执行
第一步：下一个最便宜的顶点是C

第二步：更新顶点C的邻居的开销
C顶点的邻居有：
- 顶点A（A被访问过）
- 顶点E（G被访问过）

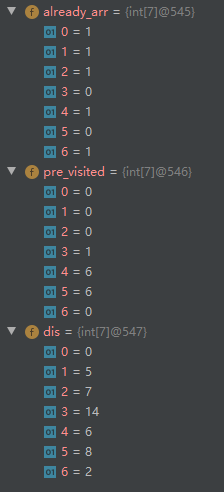
再执行
第一步：下一个最便宜的顶点是F

第二步：更新顶点F的邻居的开销
F顶点的邻居有：
- 顶点E（E被访问过）
- 顶点G（G被访问过）
- 顶点D（F到D的距离为4）

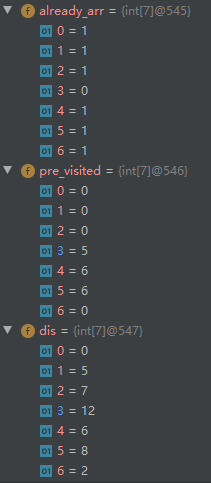
再执行
第一步：下一个最便宜的顶点是D

第二步：更新顶点D的邻居的开销
D顶点的邻居有：
- 顶点B（B被访问过）
- 顶点F（F被访问过）

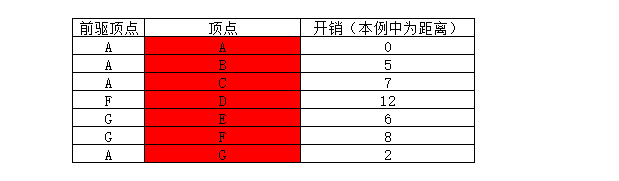
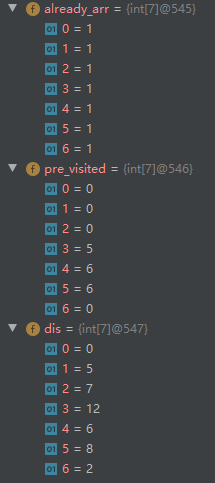
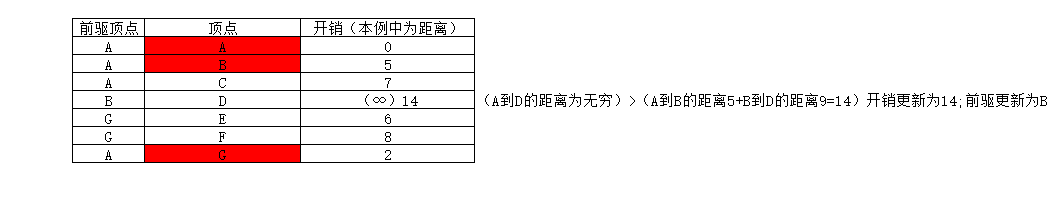
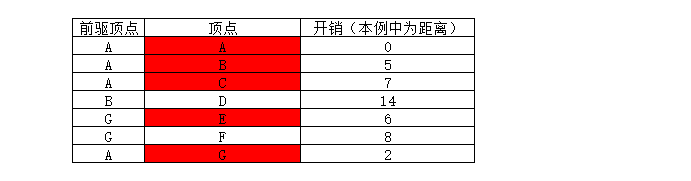
三. 计算最终路径(求从 A 到 D 的最短路径)

过程如下：
顶点D的前驱顶点为F
顶点F的前驱顶点为G
顶点G的前驱顶点为A（A为出发顶点，至此得出最短路径）

所以：
A到D的最短路径长度为12；
最短路径为：A——>G——>F——>D

代码

`package com.dyt.algorithmdemo.dijkstra;

import java.util.*;

/**

迪杰特斯拉算法
*/
public class DijkstraAlgorithm {

public static void main(String[] args) {
//顶点数组
String[] vertex = {"A", "B", "C", "D", "E", "F", "G"};
//邻接矩阵
int[][] matrix = new int[vertex.length][vertex.length];

 final int N = 65535;   //表示不可连接,没有路

 //初始化邻接矩阵
 matrix[0] = new int[]{N, 5, 7, N, N, N, 2};
 matrix[1] = new int[]{5, N, N, 9, N, N, 3};
 matrix[2] = new int[]{7, N, N, N, 8, N, N};
 matrix[3] = new int[]{N, 9, N, N, N, 4, N};
 matrix[4] = new int[]{N, N, 8, N, N, 5, 4};
 matrix[5] = new int[]{N, N, N, 4, 5, N, 6};
 matrix[6] = new int[]{2, 3, N, N, 4, 6, N};

 //创建图对象
 Graph graph = new Graph(vertex, matrix);
 graph.showGraph();

 graph.djs(0);
 graph.showDijkstra();
 //输出路径
 graph.printPath(0, 3);

}

/**

图
*/
class Graph {

//顶点数组
private String[] vertex;
//邻接矩阵
private int[][] matrix;
//访问过的顶点
private VisitedVertex visitedVertex;

public Graph(String[] vertex, int[][] matrix) {
this.vertex = vertex;
this.matrix = matrix;
}

//显示图
public void showGraph() {
for (int[] link : matrix) {
System.out.println(Arrays.toString(link));
}
}

/**
- 迪杰特斯拉算法核心代码
- @param index
  */
  public void djs(int index) {
  visitedVertex = new VisitedVertex(vertex.length, index);
  update(index); //更新index顶点到周围顶点的距离和前驱顶点
  for (int j = 1; j < vertex.length; j++) {
  index = visitedVertex.updateArr();//选择并返回新的访问顶点
  update(index);// 更新index顶点到周围顶点的距离和前驱顶点
  }
  }
//更新index下标顶点到周围顶点的距离和周围顶点的前驱顶点
public void update(int index) {
int len = 0;
//遍历我们的邻接矩阵matrix[index]行
for (int j = 0; j < matrix[index].length; j++) {
//len : 出发顶点到index顶点的距离 + 从index顶点到j顶点距离的和
len = visitedVertex.getDis(index) + matrix[index][j];
//如果j顶点没有被访问过 && 距离小于从出发顶点到j点的距离
if (!visitedVertex.in(j) && len < visitedVertex.getDis(j)) {
visitedVertex.updatePre(j, index);//更新j顶点的前驱为index顶点
visitedVertex.updateDis(j, len); //更新出发点到顶点j的距离
}
}
}

/**
- 输出路径
- @param startIndex 起点索引
- @param endIndex 终点索引
  */
  public void printPath(int startIndex, int endIndex) {
  int[] dis = visitedVertex.getDis();
  int[] pre_visited = visitedVertex.getPre_visited();
  
  String startVertex = this.vertex[startIndex];
  String endVertex = this.vertex[endIndex];
  
  //距离
  System.out.println(startVertex + "到" + endVertex + "的最短距离为：" + dis[endIndex]);
  
  //路径
  List path = new ArrayList<>();
  path.add(vertex[endIndex]);
  while (true) {
  endIndex = pre_visited[endIndex];
  path.add(vertex[endIndex]);
  if (endIndex == startIndex) {
  break;
  }
  }
  Collections.reverse(path);
  String pathInfo = "";
  for (int i = 0; i < path.size(); i++) {
  pathInfo = path.get(i);
  if (i != path.size() - 1) {
  pathInfo = pathInfo + "——>";
  }
  System.out.print(pathInfo);
  }
  System.out.println();
  }
public void showDijkstra() {
visitedVertex.show();
}

}

/**

已访问过的顶点
*/
class VisitedVertex {

//记录各个顶点是否访问过。1,表示访问过；0，表示未访问过
public int[] already_arr;
//每个下标对应的值为前一个顶点的下标
public int[] pre_visited;
//记录出发点到其他所有顶点的距离，如G点为出发点，就会记录G到其他顶点的距离
public int[] dis;

public int[] getPre_visited() {
return pre_visited;
}

public int[] getDis() {
return dis;
}

/**
- @param length 顶点个数
- @param index 出发节点索引
  */
  public VisitedVertex(int length, int index) {
  this.already_arr = new int[length];
  this.pre_visited = new int[length];
  this.dis = new int[length];
  Arrays.fill(dis, 65535);
  //设置出发节点访问过
  this.already_arr[index] = 1;
  //设置出发顶点的前驱顶点为自己
  this.pre_visited[index] = index;
  //设置出发顶点的访问距离为0
  this.dis[index] = 0;
  }
/**
- 判断index顶点是否被访问过
- @param index
- @return 访问过返回true，否则返回false
  */
  public boolean in(int index) {
  return already_arr[index] == 1;
  }
/**
- 更新出发顶点到index顶点的距离
- @param index
- @param distance
  */
  public void updateDis(int index, int distance) {
  dis[index] = distance;
  }
/**
- 更新index这个顶点的前驱顶点为pre
- @param index
- @param pre
  */
  public void updatePre(int index, int pre) {
  pre_visited[index] = pre;
  }
/**
- 返回出发顶点到index顶点的距离
- @param index
- @return
  */
  public int getDis(int index) {
  return dis[index];
  }
/**
- 继续选择并返回新的访问顶点，比如这里的 G 完后，就是 A 点作为新的访问顶点(注意不是出发顶点)
- @return
  */
  public int updateArr() {
  int min = 65535, index = 0;
  for (int i = 0; i < already_arr.length; i++) {
  //如果顶点i没有被访问过 &&
  if (already_arr[i] == 0 && dis[i] < min) {
  min = dis[i];
  index = i;
  }
  }
  //更新index顶点被访问过
  already_arr[index] = 1;
  return index;
  }
public void show() {
System.out.println("");
//输出已访问顶点already_arr
System.out.println("已访问顶点already_arr");
for (int i : already_arr) {
System.out.print(i + " ");
}
System.out.println();
System.out.println("前驱顶点数组pre_visited");
//输出前驱顶点数组pre_visited
for (int i : pre_visited) {
System.out.print(i + " ");
}
System.out.println();
System.out.println("输出距离数组========");
//输出距离数组
for (int i : dis) {
System.out.print(i + " ");
}
System.out.println();
}

}
`

posted @ 2020-08-19 16:22 &呆呆& 阅读(1198) 评论(0) 收藏举报

刷新页面返回顶部