PTA1-3总结
- 前言
本次博客对pta前三次作业进行多方面总结,对知识点,题量,难度等方面进行分析。第一次作业题量比较多,但大都比较容易,学习了许多基础的方法,除了最后一题因为误差问题卡了一下,其他题目也都顺利完成。还是采用面向过程的思想,第二次作业依旧采用面向过程去写,难度也不是很大,第二题因为自己写了太多自增变量嵌入在for循环当中,导致打印时出错找了很久这个问题,还有就是数组概念也更加清晰。第三次作业难度明显加大了,难度比前两次提升了不少,老师要求采用面向对象去写,前两次都是采用面向过程去写题目,突然要面向对象,一开始真是无从下手,经过自己查阅与询问同学,花费大量时间,再到后来能慢慢去写各个类和方法,创建新对象去调用其他类的方法,花了大量的时间去掌握,虽然还不是特别熟练,但是因此自己的java能力提高了不少。
- 设计与分析
一、
7-6 学号识别
作者 蔡轲
-
单位 南昌航空大学
学校的学号由8位数字组成,前两位是入学年份(省略了20);第3、4位是学院编号,01代表材料学院,02代表机械学院,03代表外语学院,20代表软件学院;第5、6位是学院内部班级编号,最后两位是班级内部学号。如:18011103,入学年份是2018年,材料学院,11班,03号
输入格式:
8位数字组成的学号。例如:18011103
注意:输入学号不是8位或者学院编号不是01、02、03、20其中之一,属于非法输入输出格式:
学号每一项的完整说明。例如:
入学年份:2018年
学院:材料学院
班级:11
学号:03注意:如非法输入,输出“Wrong Format"
import java.util.Scanner; public class Main{ public static void main(String[] args){ // String x; String xn,xy,bj,xh;//分别代表年份,学院编号,学院内部班级编号,班级内部学号 Scanner sc = new Scanner(System.in); String x=sc.next(); int length=x.length(); if(x.length()!=8){ System.out.println("Wrong Format"); return; } else{ xn=x.substring(0,2); xy=x.substring(2,4); bj=x.substring(4,6); xh=x.substring(6,8); } int value = Integer.parseInt(x.substring(2,4)); //System.out.println("入学年份:"+"20"+x.substring(0,2)+"年"); if(value!=01&&value!=02&&value!=03&&value!=20){ System.out.println("Wrong Format"); return; } System.out.println("入学年份:"+"20"+x.substring(0,2)+"年"); if(value==01){ System.out.println("学院:材料学院"); }else if(value==02){ System.out.println("学院:机械学院"); }else if(value==03){ System.out.println("学院:外语学院"); }else if(value==20){ System.out.println("学院:软件学院"); }else{ System.out.println("Wrong Format"); } System.out.println("班级:"+x.substring(4,6)); System.out.print("学号:"+x.substring(6,8)); } }
7-7 判断三角形类型
输入三角形三条边,判断该三角形为什么类型的三角形。
输入格式:
在一行中输入三角形的三条边的值(实型数),可以用一个或多个空格或回车分隔,其中三条边的取值范围均为[1,200]。
输出格式:
(1)如果输入数据非法,则输出“Wrong Format”;
(2)如果输入数据合法,但三条边不能构成三角形,则输出“Not a triangle”;
(3)如果输入数据合法且能够成等边三角形,则输出“Equilateral triangle”;
(3)如果输入数据合法且能够成等腰直角三角形,则输出“Isosceles right-angled triangle”;
(5)如果输入数据合法且能够成等腰三角形,则输出“Isosceles triangle”;
(6)如果输入数据合法且能够成直角三角形,则输出“Right-angled triangle”;
(7)如果输入数据合法且能够成一般三角形,则输出“General triangle”。
import java.util.*;
public class Main{
public static void main(String[] args){
Scanner input = new Scanner(System.in);
double x=input.nextDouble();
double y=input.nextDouble();
double z=input.nextDouble();
if(x<1||x>200||y<1||y>200||z<1||z>200){
System.out.println("Wrong Format");
return;
}else if((x+y<=z)||(x+z<=y)||(y+z<=x))
{
System.out.println("Not a triangle");
return;
}
else if(x==y&&y==z&&x==z){
System.out.println("Equilateral triangle");
return;
}else if(Math.abs(x*x+y*y-z*z)<0.000001){
if(x==y){
System.out.println("Isosceles right-angled triangle");
}
else {
System.out.println("Right-angled triangle");
}
}else if(Math.abs(y*y+z*z-x*x)<0.000001){
if(y==z){
System.out.println("Isosceles right-angled triangle");
}
else {
System.out.println("Right-angled triangle");
}
return;
}else if(Math.abs(x*x+z*z-y*y)<0.000001){
if(x==z){
System.out.println("Isosceles right-angled triangle");}
else {
System.out.println("Right-angled triangle");
}
return;}
else if(x==y||y==z||x==z){
System.out.println("Isosceles triangle");
return;
}
else {
System.out.println("General triangle");
}
}
}
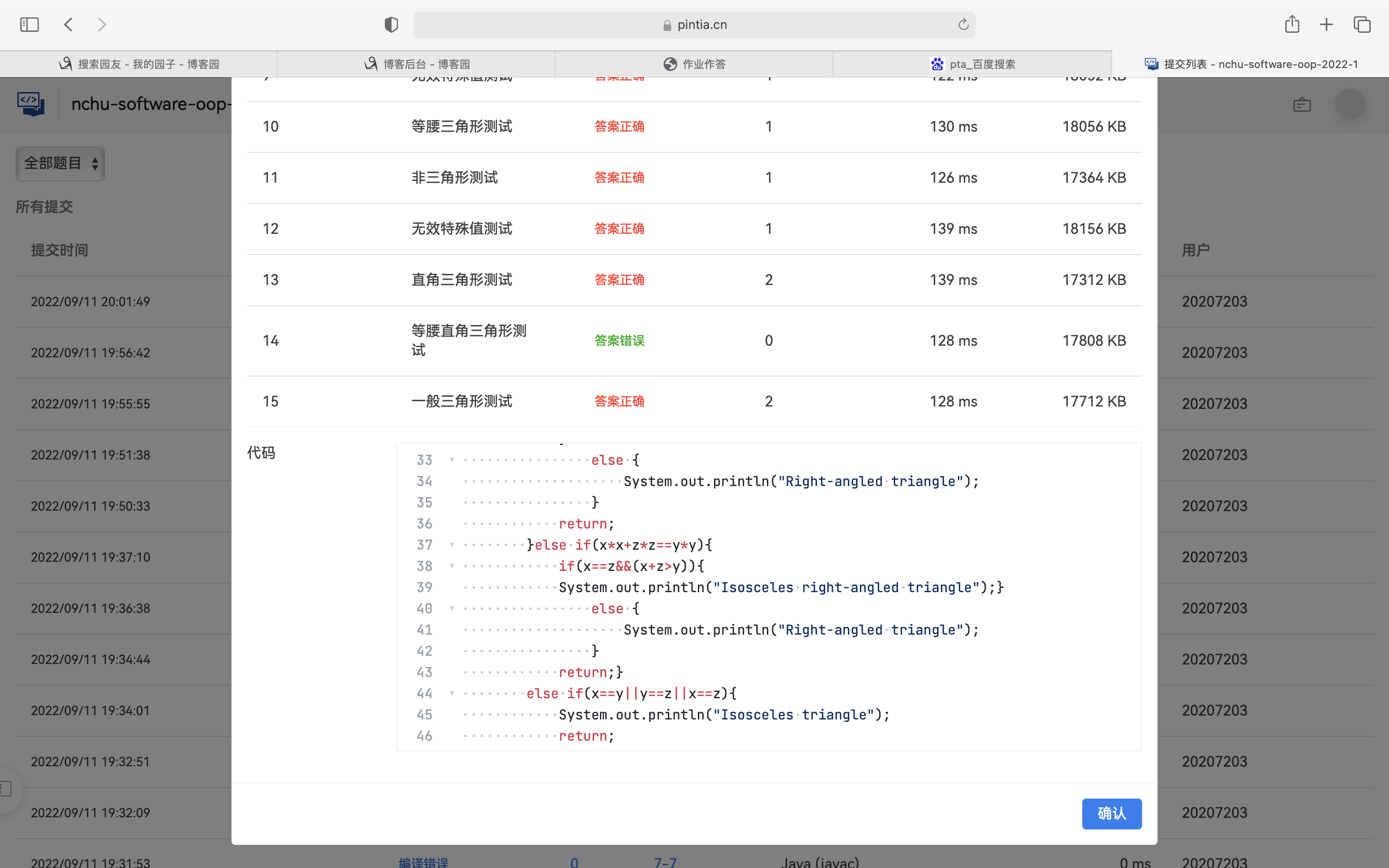
踩坑心得:第一次作业题目偏简单,但是学习了一些比较基础的方法,例如Integer.psrseInt()整型数据类型Integer转换为基本数据类型int和substring()字符串截取方法,主要在 7-6 体现。还有就是注意精度(double和float的使用),以及证明直角三角形存在误差。可以设置一个很小的误差比如0.000001.
pta二、
学校学生学号格式定义如下:
2位年级号+2位学院号+2位班级号+2位序号,如19041103,
编写程序处理用全院学生学号连接起来的长字符串,学院编号为20,包括17、18、19、20四个年级,请从字符串中提取特定两个班级202017班、202061班同学的学号后四位输出,输出编号之间用空格分隔,不换行。
注意:需要排除非法输入。
输入格式:
全院学生学号组成的长字符串(学号之间无分隔)
学号格式定义如下:
2位年级号+2位学院号+2位班级号+2位序号,如19041103,
输出格式:
特定两个班级202017班、202061班同学的学号后四位
如:1701 6103 1704
import java.util.*;
public class Main{
public static void main(String[] args){
String nj,xy,bj,xh;
Scanner sc = new Scanner(System.in);
String s=sc.nextLine();
for(int i=0;i<s.length();i++){
char ch=s.charAt(i);
if(ch<'0'||ch>'9'){
System.out.print("Wrong Format");
return;
}
}
if(s.length()%8!=0){
System.out.print("Wrong Format");
return;
}
int count=0;
for(int i=0;i<s.length();i+=8){
int value=Integer.parseInt(s.substring(i,i+6));
int last=Integer.parseInt(s.substring(i+4,i+8));
if(value==202017||value==202061){
if(count==1){
System.out.print(" ");}
System.out.print(last);
count=1;
}
}
}
}
RS232是串口常用的通信协议,在异步通信模式下,串口可以一次发送5~8位数据,收发双方之间没有数据发送时线路维持高电平,相当于接收方持续收到数据“1”(称为空闲位),发送方有数据发送时,会在有效数据(5~8位,具体位数由通信双方提前设置)前加上1位起始位“0”,在有效数据之后加上1位可选的奇偶校验位和1位结束位“1”。请编写程序,模拟串口接收处理程序,注:假定有效数据是8位,奇偶校验位采用奇校验。
输入格式:
由0、1组成的二进制数据流。例如:11110111010111111001001101111111011111111101111
输出格式:
过滤掉空闲、起始、结束以及奇偶校验位之后的数据,数据之前加上序号和英文冒号。
如有多个数据,每个数据单独一行显示。
若数据不足11位或者输入数据全1没有起始位,则输出"null data",
若某个数据的结束符不为1,则输出“validate error”。
若某个数据奇偶校验错误,则输出“parity check error”。
若数据结束符和奇偶校验均不合格,输出“validate error”。
如:11011或11111111111111111。
例如:
1:11101011
2:01001101
3:validate error
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String a = sc.nextLine();
char[] b=new char[500];
int x=0;
int y=1;
int count=0;
for(int i=0;i<a.length();i++){
b[i]=a.charAt(i); //字符串转化为整型数字
if(b[i]=='1'){
count++;//数据‘1’空闲位自增
}
}if(count==a.length()||a.length()<11){
System.out.print("null data");//数据全为1或者不足11位
}
else {
for(int i=0;i<a.length();i++){
if(b[i]=='0'&&i+10<a.length()){
String str=a.substring(i+1,i+9);//字符串截取
for(int j=i+1;j<i+9;j++)
{
if(b[j]=='1'){
// int x=0;
x++;//记录1的个数进行奇偶校验
}
}
// int y=1;
if(b[i+10]!='1'){
System.out.println(y+":"+"validate error");
y++;
}
else if(x%2!=1&&b[i+9]=='0'){
System.out.println(y+":"+"parity check error");
y++;
}
else if (x%2==1&&b[i+9]=='1')
{
System.out.println(y+":"+"parity check error");
y++;
}
else if(x%2==1&&b[i+9]=='0'&&b[i+10]=='1'){
System.out.println(y+":"+str);
y++;
}else if(x%2==0&&b[i+9]=='1'&&b[i+10]=='1'){
System.out.println(y+":"+str);
y++;
}
i=i+10;//11一个循环
x=0;
}
}
}
}
}
可以看到这次代码最大深度以及平均深度超出了良好范围,一个函数当中包含很多函数语句。
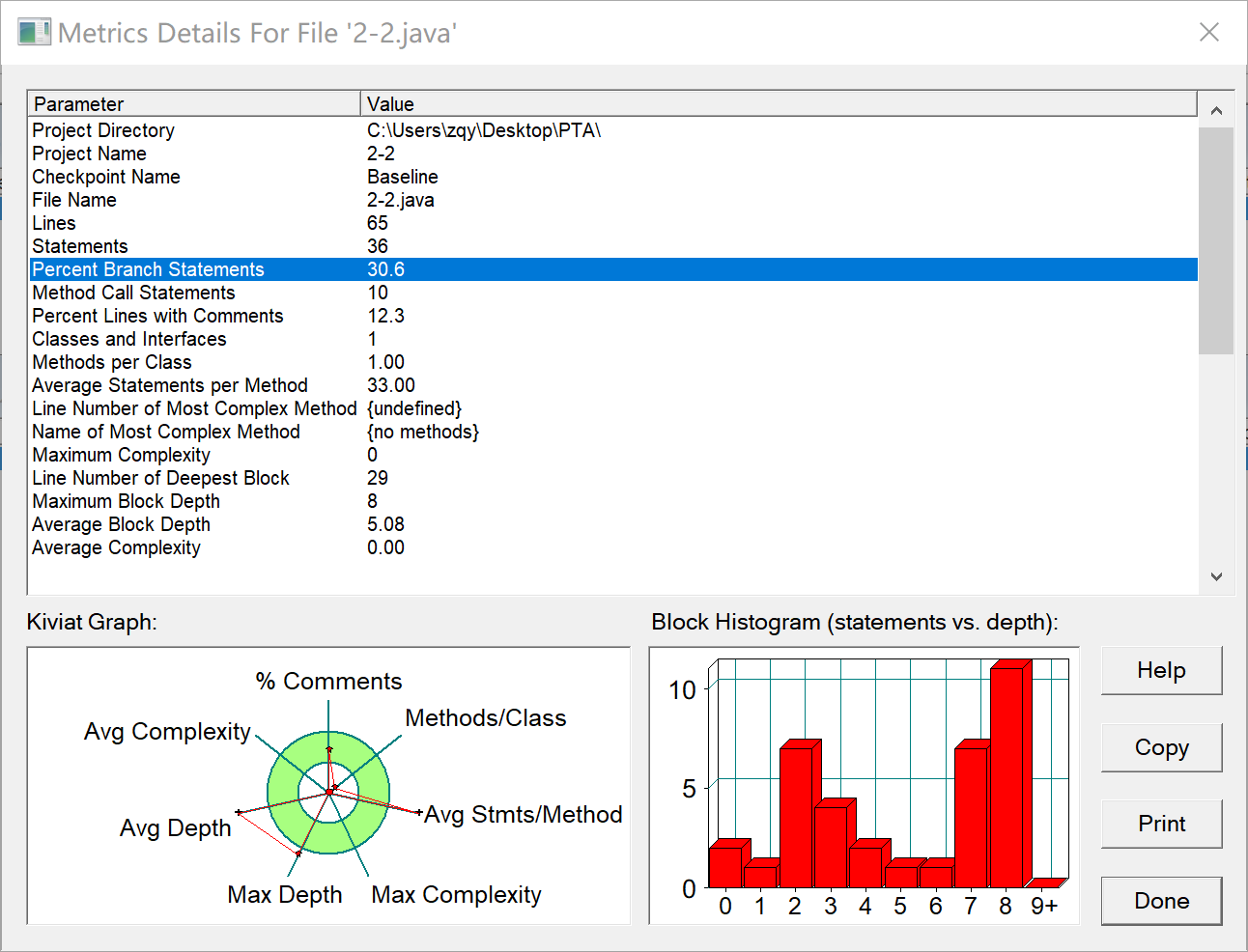
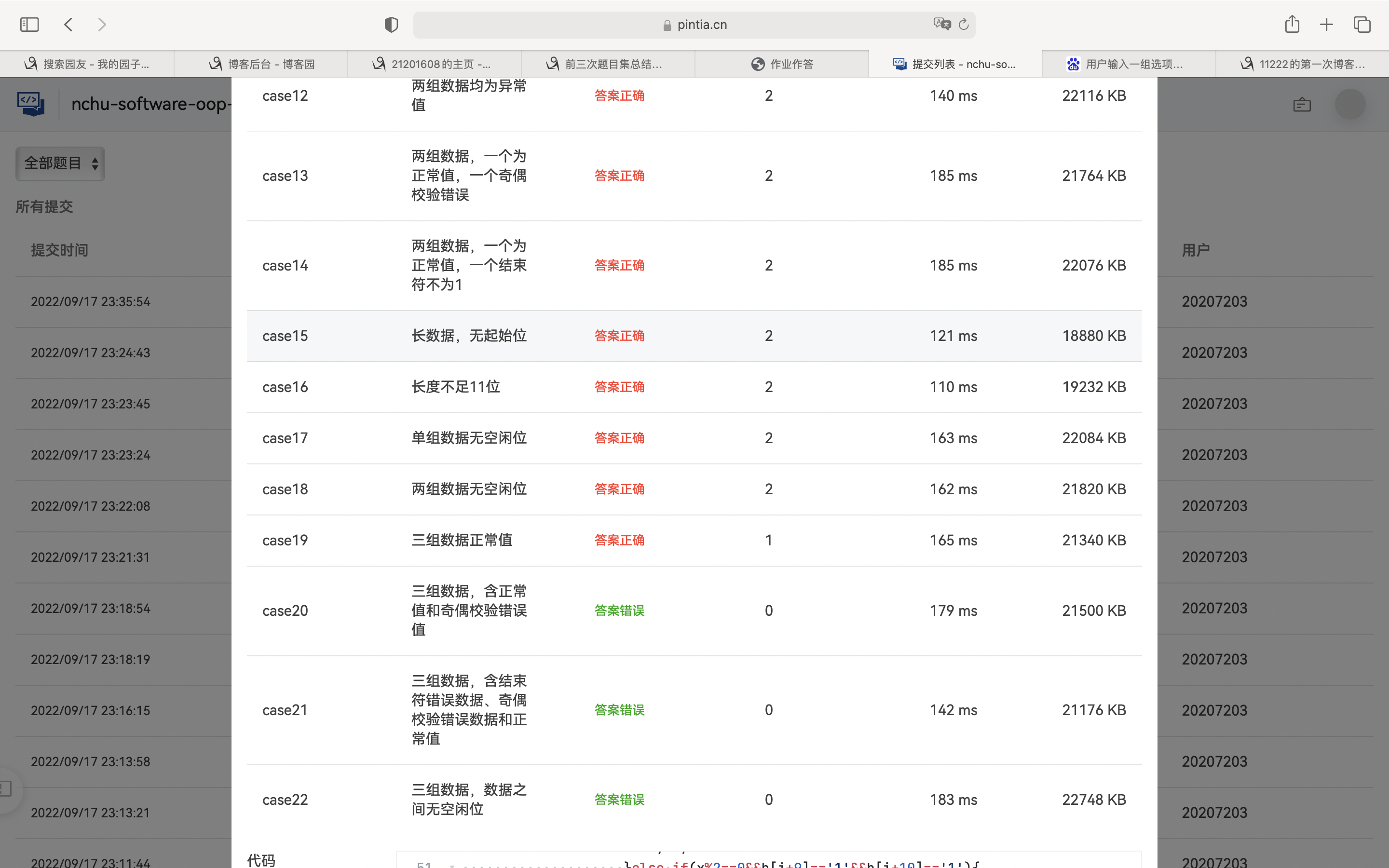
错误为自增变量设置导致在for循环当中没有变回初值,后面在第二层循环外给变量重新赋值最后测试点通过
踩坑心得:第二次作业难度提升了一点点,在第二次作业中用ASCII码表用的较为频繁,用了charAt()方法(字符的索引),主要是判断格式输入是否正确,a-z,A-Z以及1-9。还有就是next()以及nextLine()两个之间的区别。next()一定要读取到有效字符后才可以结束输入,对输入有效字符之前遇到的空格键、Tab键或Enter键等结束符,next()方法会自动将其去掉,只有在输入有效字符之后,next()方法才将其后输入的空格键、Tab键或Enter键等视为分隔符或结束符。比如,在控制台输入“ gjm gjm ”时,一次next()读入进来的仅仅是"gjm"。它不能得到带空格的字符串的。nextLine()方法的结束符只是Enter键,即nextLine()方法返回的是Enter键之前的所有字符。比如,在控制台输入“ gjm gjm ”时,一次nextLine()读入进来的结果是" gjm gjm "。它是可以得到带空格的字符串的。在第三题当中因为空格这一区别,先是用的next(),导致一个测试点一直没过,最后问了室友才知道要用nextLine()。
改进建议: 对自增变量多一个心眼或者写好注释,就不会在调试的时候一直发现不了错误,特别是嵌套在for循环语句当中的变量。
pta三、
输入连个点的坐标,计算两点之间的距离
输入格式:
4个double类型的实数,两个点的x,y坐标,依次是x1、y1、x2、y2,两个点的坐标之间以空格分隔,每个点的x,y坐标以英文“,”分隔。例如:0,0 1,1或0.1,-0.3 +3.5,15.6。
若输入格式非法,输出"Wrong Format"。
若输入格式合法但坐标点的数量超过两个,输出“wrong number of points”。
输出格式:
计算所得的两点之间的距离。例如:1.4142135623730951
- 设计与分析
设计点和输入两个类,创造两个点对象,计算距离。
import java.util.*;
public class Main{
public static void main(String[] args){
Scanner input = new Scanner(System.in);
double s=0;
// String l=input.nextLine();
Input x=new Input();
x.l=input.nextLine();
Dian p=new Dian();
Dian p1=new Dian();//创造一个使用distance方法的对象,子类的无参数构造方法
Dian p2=new Dian();
if(x.shuru()==0){
System.out.print("Wrong Format");
}else if(x.shuru()==1){
System.out.print("wrong number of points");
}else{
p1.setX(x.getX(0));
p1.setY(x.getY(0));
p2.setX(x.getX(1));
p2.setY(x.getY(1));
s=p.distance(p1,p2);
System.out.print(s);
}
}
}
class Dian{
private double x,y;//私有化,需要设定的方法 对象才能拥有相应属性
public double distance(Dian p1,Dian p2){
double s;
s=Math.sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y));
return s;
}
public double getX(){
return x;
}
public double getY() {
return y;
}
public void setX(double x){
this.x=x;
}
public void setY(double y){
this.y=y;
}
public Dian(){
super();//子类无参数构造器
}
}
class Input{
String l;
int shuru(){
String dian[]=l.split(" ");
String x[]=null;
for(String i:dian){
x=i.split(",");
for(String j:x){
if (!j.matches("^[+-]?(0|(0\\.\\d+)?|[1-9]*(\\.\\d+)?)$")) {
// System.out.print("Wrong Format");
return 0;
}
}
}
if(dian.length!=2){
// System.out.print("wrong number of points");
return 1;
}
return 2;
}
double getX(int a){
String[] dian =l.split(" ");
String[] num=dian[a].split(",");
return Double.parseDouble(num[0]);
}
double getY(int a){
String[] dian =l.split(" ");
String[] num=dian[a].split(",");
return Double.parseDouble(num[1]);
}
}
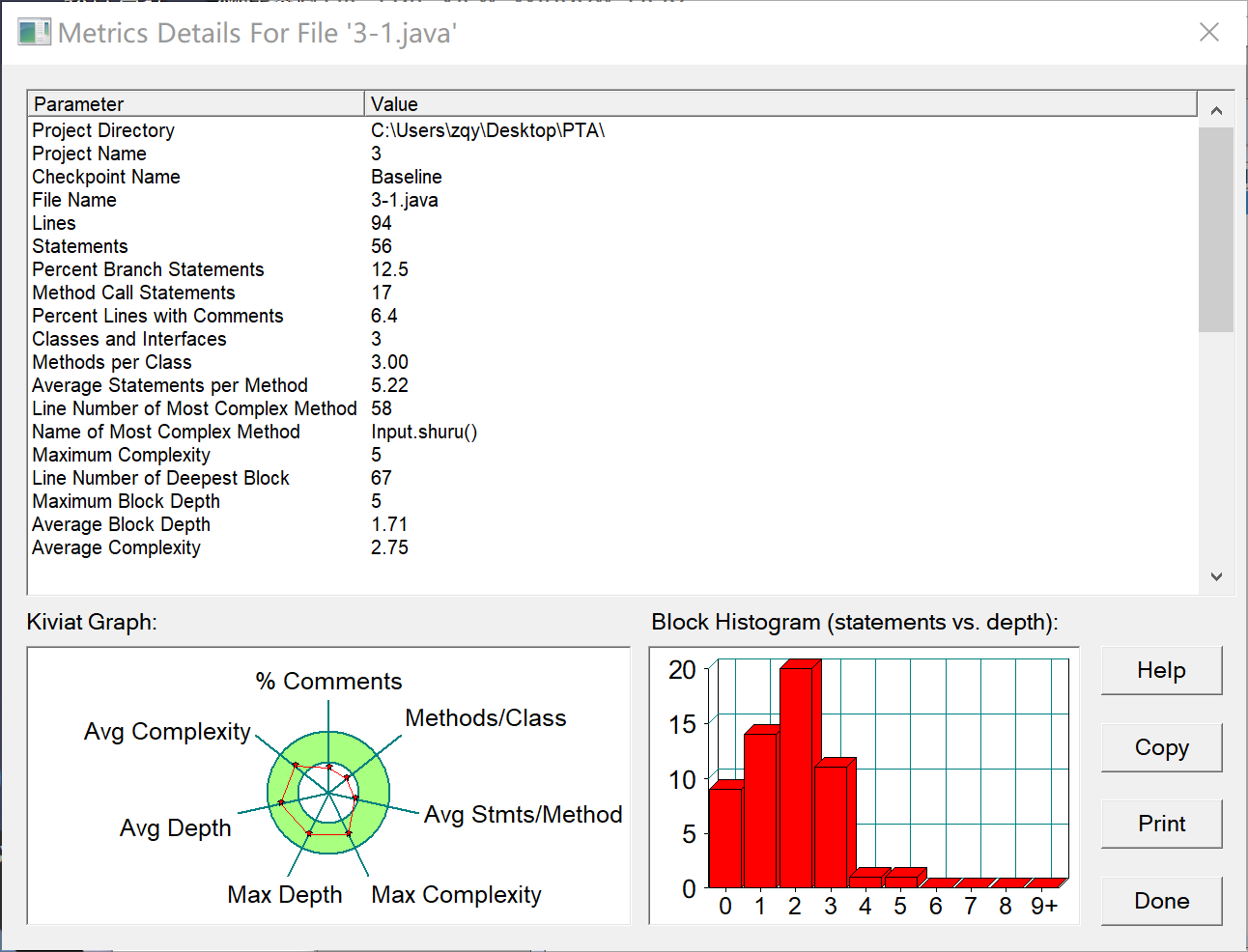
踩坑心得:第一题代码长度不长,所用的类和方法也比较简单,合法输入以及获取点,刚开始写再回过头来发现其实一个类就够了,第一题只是预热,所以可以从上图看到代码各方面都比较良好,复杂度不高。
改进建议:非法输入可以用正则表达式,简单精炼,出错率较低。
用户输入一组选项和数据,进行与直线有关的计算。选项包括:
1:输入两点坐标,计算斜率,若线条垂直于X轴,输出"Slope does not exist"。
2:输入三个点坐标,输出第一个点与另外两点连线的垂直距离。
3:输入三个点坐标,判断三个点是否在一条线上,输出true或者false。
4:输入四个点坐标,判断前两个点所构成的直线与后两点构成的直线是否平行,输出true或者false.
5:输入四个点坐标,计算输出前两个点所构成的直线与后两点构成的直线的交点坐标,x、y坐标之间以英文分隔",",并输出交叉点是否在两条线段之内(不含四个端点)的判断结果(true/false),判断结果与坐标之间以一个英文空格分隔。若两条线平行,没有交叉点,则输出"is parallel lines,have no intersection point"。
输入格式:
基本格式:选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。
例如:1:0,0 1,1
如果不符合基本格式,输出"Wrong Format"。
如果符合基本格式,但输入点的数量不符合要求,输出"wrong number of points"。
不论哪个选项,如果格式、点数量都符合要求,但构成任一条线的两个点坐标重合,输出"points coincide",
- 设计与分析
设计点和线两个类,判断非法输入用正则表达式编写,if else 语句判断题目五种情况,首先判断输入点的个数是否正确,再执行下一步,调用各种方法实现题目。
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String str = sc.nextLine();
String[] a = str.split(":");
if(a[0].isEmpty()||a[0].equals("")){
System.out.println("Wrong Format");
return;
}
int option = Integer.parseInt(a[0]);
String[] points = a[1].split(" ");
// System.out.println(points[0]);
// System.out.println(points[1]);
if(!str.matches("^[1-5]:(([+-]?(0(\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?)),([+-]?(0(\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?)) )*(([+-]?(0(\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?)),([+-]?(0(\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?))) *"))
{
System.out.println("Wrong Format");
return;
} if(option == 1){
if (points.length != 2) {
System.out.print("wrong number of points");
return;
}
Point point1 = new Point();
Point point2 = new Point();
for (int i = 0;i < 2; i++) {
String[] p = points[i].split(",");
String x1 = p[0];
String y1 = p[1];
if(i == 0){
point1.input(Double.parseDouble(x1),Double.parseDouble(y1));
}
if(i == 1){
point2.input(Double.parseDouble(x1),Double.parseDouble(y1));
}
}
Line line = new Line();
line.p1 = point1;
line.p2 = point2;
if(point1.check_point(point2)){
System.out.println("points coincide");
return;
}
if(!line.check_slope()){
System.out.println("Slope does not exist");
return;
}
System.out.println(line.xielv());
}
if(option == 2){
if (points.length != 3) {
System.out.print("wrong number of points");
return;
}
Point point1 = new Point();
Point point2 = new Point();
Point point3 = new Point();
for (int i = 0;i < 3; i++) {
String[] p = points[i].split(",");
String x1 = p[0];
String y1 = p[1];
if(i == 0){
point1.input(Double.parseDouble(x1),Double.parseDouble(y1));
}
if(i == 1){
point2.input(Double.parseDouble(x1),Double.parseDouble(y1));
}
if(i == 2){
point3.input(Double.parseDouble(x1),Double.parseDouble(y1));
}
}
Line line = new Line();
line.p1 = point2;
line.p2 = point3;
if(point2.check_point(point3)){
System.out.println("points coincide");
return;
}
if(!line.check_slope()){
System.out.println(Math.abs(point1.getX()-point2.getX()));
return;
}
System.out.println(line.linedistance(point1));
}
if(option == 3){
if (points.length != 3) {
System.out.print("wrong number of points");
return;
}
Point point1 = new Point();
Point point2 = new Point();
Point point3 = new Point();
for (int i = 0;i < 3; i++) {
String[] p = points[i].split(",");
String x1 = p[0];
String y1 = p[1];
if(i == 0){
point1.input(Double.parseDouble(x1),Double.parseDouble(y1));
}
if(i == 1){
point2.input(Double.parseDouble(x1),Double.parseDouble(y1));
}
if(i == 2){
point3.input(Double.parseDouble(x1),Double.parseDouble(y1));
}
}
Line line = new Line();
line.p1 = point2;
line.p2 = point3;
//if(point2.check_point(point3)||point1.check_point(point2)||point1.check_point(point3)){
// System.out.println("points coincide");
// return;
// }
if(!line.check_slope()){
System.out.println(point1.getX()==point2.getX());
return;
}else
System.out.println(line.if_on_line(point1));
}
if(option == 4 || option == 5){
if (points.length != 4) {
System.out.print("wrong number of points");
return;
}
Point point1 = new Point();
Point point2 = new Point();
Point point3 = new Point();
Point point4 = new Point();
for (int i = 0;i < 4; i++) {
String[] p = points[i].split(",");
String x1 = p[0];
String y1 = p[1];
if(i == 0){
point1.input(Double.parseDouble(x1),Double.parseDouble(y1));
}
if(i == 1){
point2.input(Double.parseDouble(x1),Double.parseDouble(y1));
}
if(i == 2){
point3.input(Double.parseDouble(x1),Double.parseDouble(y1));
}
if(i == 3){
point4.input(Double.parseDouble(x1),Double.parseDouble(y1));
}
}
Line line1 = new Line();
Line line2 = new Line();
line1.p1 = point1;
line1.p2 = point2;
line2.p1 = point3;
line2.p2 = point4;
if (line1.p1.check_point(line1.p2)||line2.p1.check_point(line2.p2)){
System.out.println("points coincide");
return;
}
if(option == 4){
if(!line1.check_slope()&&!line2.check_slope())
{
System.out.println("true");
return;
}else if (!line1.check_slope()&&line2.check_slope())
{
System.out.println("false");
return;
}else if (line1.check_slope()&&!line2.check_slope())
{
System.out.println("false");
return;
}else
System.out.println(line1.parallel(line2) != -1 );
}
if(option == 5){
if(line1.parallel(line2) != -1){
System.out.println("is parallel lines,have no intersection point");
return;
}
Point point = line1.jiaodian(line2);
if(point.x==point1.x&&point.y==point1.y){
System.out.print(point.getX() + "," + point.getY() + " " +"false");
}else if(point.x==point2.x&&point.y==point2.y){
System.out.print(point.getX() + "," + point.getY() + " " +"false");
}else if(point.x==point3.x&&point.y==point3.y){
System.out.print(point.getX() + "," + point.getY() + " " +"false");
}else if(point.x==point4.x&&point.y==point4.y){
System.out.print(point.getX() + "," + point.getY() + " " +"false"); 、
}else
System.out.println(point.getX() + "," + point.getY() + " " +(line1.if_in_line(point) || line2.if_in_line(point)));
}
}
}
}
class Point {
String l;
public double x, y;
//读入x y 的值//
public void input(double x, double y) {
this.x = x;
this.y = y;
}
//读取x的值//
public double getX() {
return x;
}
//读取y的值//
public double getY() {
return y;
}
//计算两点的距离//
public double calculate_distance(Point p) {
return Math.sqrt((x - p.x) * (x - p.x) + (y - p.y) * (y - p.y));
}
//检查线的两点是否重合//
public boolean check_point(Point p) {
boolean flag = false;
if (Math.abs(x - p.getX()) < 1e-16 && Math.abs(y - p.getY()) < 1e-16)
flag = true;
return flag;
}
}
class Line {
Point p1 = new Point();
Point p2 = new Point();
double a,b,c;
//检查线段的斜率是否存在//
public boolean check_slope() {
boolean flag = true;
if (Math.abs(p1.getX() - p2.getX()) < 1e-15) {
flag = false;
}
return flag;
}
//计算线段的斜率//
public double xielv() {
return (p1.getY() - p2.getY()) / (p1.getX() - p2.getX());
}
//计算点到直线的距离//
public double linedistance(Point l) {
zcline(this);
double distance;
// if (if_on_line(l)) {
// distance = 0;//在直线上
//} else {
distance=Math.abs(a*l.getX()+b*l.getY()+c)/Math.sqrt(a*a+b*b);
// distance = Math.abs(a.getX() * p1.getY() + p1.getX() * p2.getY() + p2.getX() * a.getY() - a.getX() * p2.getY() - p1.getX() * a.getY() - p2.getX() * p1.getY()) / p1.calculate_distance(p2);
//}
return distance;
}
//判断点是否再直线上//
public boolean if_on_line(Point p) {
boolean flag = false;
Line l2 = new Line();
l2.p1 = p1;
l2.p2 = p;
if (this.xielv() == l2.xielv()) {
flag = true;
}
return flag;
}
//判断点是否在线段内//
//在线段内返回true,在线段外返回false//
public boolean if_in_line(Point p) {
boolean flag = false;
if (if_on_line(p)) {
if (p.calculate_distance(p1) > p1.calculate_distance(p2) || p.calculate_distance(p2) > p1.calculate_distance(p2))
return flag;
else {
flag = true;
}
return flag;
}
return flag;
}
//判断两直线是否平行//
//若两直线平行返回1,若两直线重合返回0,若两直线相交返回-1
public int parallel(Line l) {//判断是否平行
int count;
if (this.xielv() != l.xielv()) {
count = -1;
} else {
if (l.linedistance(p1) == 0) {
count = 0;
} else {
count = 1;
}
}
return count;
}
public void zcline(Line l){
l.a= l.p1.getY()- l.p2.getY();
l.b= l.p2.getX()-l.p1.getX();
l.c= l.p2.getY()*l.p1.getX()-l.p2.getX()*l.p1.getY();
}
//计算两直线交点,返回Point//
public Point jiaodian(Line l) {
zcline(l);
zcline(this);
Point p = new Point();
double x,y;
x=(b*l.c-l.b*c)/(a*l.b-l.a*b);
y=(a*l.c-l.a*c)/(l.a*b-a*l.b);
p.input(x,y);
return p;
}
}
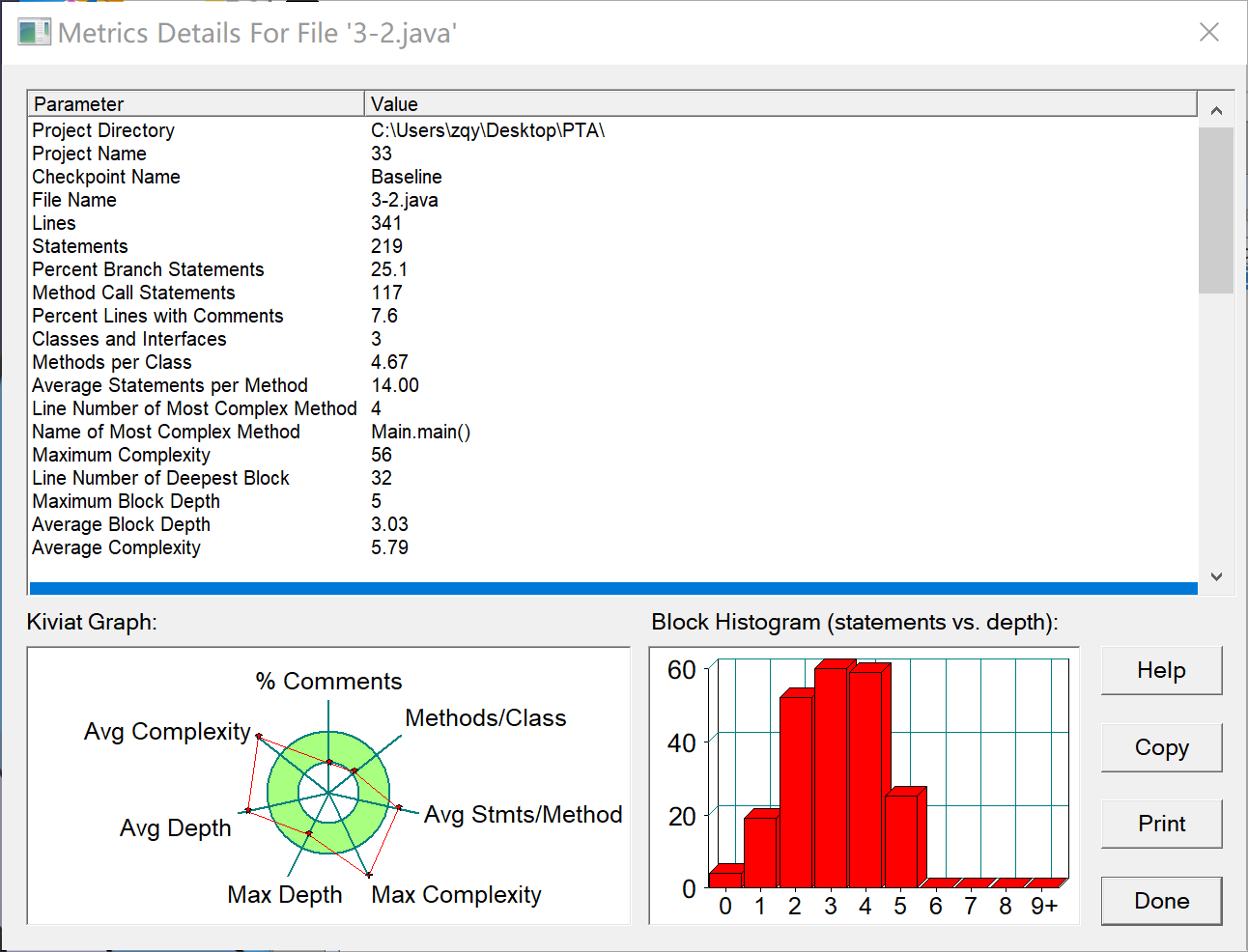
踩坑心得:第二题相比第一题难度提升很大,用边和点两个类,以及要熟悉正则表达式的编写,边和点两个类中含有较多种方法,可以从上图可知,代码的圈复杂度明显增大,平均深度也较大,代码水平质量不是很高,第一次用面向对象的方法写还是比较吃力,用了较多的if else语句。题目并没有过全部测试点,输入所有测试案列依旧有测试点过不去,对类的方法属性掌握不够熟练。
改进建议:减少if else 语句的运用,擅长于用少而精炼的方法来排出非法输入以及特殊情况,以及对类中方法的作用性更加明了。
用户输入一组选项和数据,进行与三角形有关的计算。选项包括:
1:输入三个点坐标,判断是否是等腰三角形、等边三角形,判断结果输出true/false,两个结果之间以一个英文空格符分隔。
2:输入三个点坐标,输出周长、面积、重心坐标,三个参数之间以一个英文空格分隔,坐标之间以英文","分隔。
3:输入三个点坐标,输出是钝角、直角还是锐角三角形,依次输出三个判断结果(true/false),以一个英文空格分隔,
4:输入五个点坐标,输出前两个点所在的直线与三个点所构成的三角形相交的交点数量,如果交点有两个,则按面积大小依次输出三角形被直线分割成两部分的面积。若直线与三角形一条线重合,输出"The point is on the edge of the triangle"
5:输入四个点坐标,输出第一个是否在后三个点所构成的三角形的内部(输出in the triangle/outof triangle)。
必须使用射线法,原理:由第一个点往任一方向做一射线,射线与三角形的边的交点(不含点本身)数量如果为1,则在三角形内部。如果交点有两个或0个,则在三角形之外。若点在三角形的某条边上,输出"on the triangle"
输入格式:
基本格式:选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。点的x、y坐标之间以英文","分隔,点与点之间以一个英文空格分隔。
输出格式:
基本输出格式见每种选项的描述。
异常情况输出:
如果不符合基本格式,输出"Wrong Format"。
如果符合基本格式,但输入点的数量不符合要求,输出"wrong number of points"。
如果输入的三个点无法构成三角形,输出"data error"。
注意:输出的数据若小数点后超过6位,只保留小数点后6位,多余部分采用四舍五入规则进到最低位。小数点后若不足6位,按原始位数显示,不必补齐。例如:1/3的结果按格式输出为 0.333333,1.0按格式输出为1.0
选项4中所输入线的两个点坐标重合,输出"points coincide",
- 设计与分析
创造点、线、三角形三个类。点构成边,边构成三角形,再根据三角形的性质,判断能否构成三角形,直线与三角形的三条边有没有交点,有几个交点,再根据面积公式算出面积。用左边轴辅助解题会更好。
下面为三个类的设计,主类与前一题大差不差
class Point {
String l;
public double x;
public double y;
//读入x y 的值//
public void input(double x, double y) {
this.x = x;
this.y = y;
}
//读取x的值//
public double getX() {
return x;
}
//读取y的值//
public double getY() {
return y;
}
public boolean check_point(Point p) {
boolean flag = false;
if (Math.abs(x - p.getX()) < 1e-16 && Math.abs(y - p.getY()) < 1e-16)
flag = true;
return flag;
}
public double calculate_distance(Point p) //点的距离
{
return Math.sqrt((x - p.x) * (x - p.x) + (y - p.y) * (y - p.y));
}
}
class Line {
Point p3 = new Point();
double a, b, c;
Point p1 = new Point();
Point p2 = new Point();
//检查线段的斜率是否存在//
public boolean check_slope() {
boolean flag = true;
if (Math.abs(p1.getX() - p2.getX()) < 1e-15) {
flag = false;
}
return flag;
}
//点到直线距离
public double linedistance(Point l) {
zcline(this);
double distance;
distance = Math.abs(a * l.getX() + b * l.getY() + c) / Math.sqrt(a * a + b * b);
return distance;
}
//计算线段的斜率//
public double xielv() {
return (p1.getY() - p2.getY()) / (p1.getX() - p2.getX());
}
public boolean if_on_line(Point p) {
boolean flag = false;
Line l2 = new Line();
l2.p1 = p1;
l2.p2 = p;
if (Math.abs(this.a * p.x + this.b * p.y + this.c) < 1e-15) {
flag = true;
}
return flag;
}
//判断点是否在线段内//
//在线段内返回true,在线段外返回false
public boolean if_in_line(Point p) {
boolean flag = false;
if (if_on_line(p)) {
if (p.calculate_distance(p1) > p1.calculate_distance(p2) || p.calculate_distance(p2) > p1.calculate_distance(p2))
return flag;
else {
flag = true;
}
return flag;
}
return flag;
}
//判断两直线是否平行//
//若两直线平行返回1,若两直线重合返回0,若两直线相交返回-1
public int parallel(Line l) {//判断是否平行
int count;
if (this.xielv() != l.xielv()) {
count = -1;
} else {
if (l.linedistance(p1) == 0) {
count = 0;
} else {
count = 1;
}
}
return count;
}
//直线一般表达式
public void zcline(Line l) {
l.a = l.p1.getY() - l.p2.getY();
l.b = l.p2.getX() - l.p1.getX();
l.c = l.p2.getY() * l.p1.getX() - l.p2.getX() * l.p1.getY();
}
//计算两直线交点,返回Point
public Point jiaodian(Line l) {
zcline(l);
zcline(this);
Point p = new Point();
double x, y;
x = (b * l.c - l.b * c) / (a * l.b - l.a * b);
y = (a * l.c - l.a * c) / (l.a * b - a * l.b);
p.input(x, y);
return p;
}
}
class Triangle {
Point p1 = new Point();
Point p2 = new Point();
Point p3 = new Point();
//j检查能否构成三角形
public boolean checktriangle() {
boolean flag = true;
if (Math.abs(p1.calculate_distance(p2) - p1.calculate_distance(p3)) < p2.calculate_distance(p3)
&& Math.abs(p1.calculate_distance(p3) + p1.calculate_distance(p2)) > p2.calculate_distance(p3)) {
flag = false;
}
return flag;
}
//判断为等腰三角形==0还是等边三角形==1
public int shape_what_triangle() {
int shape = 0;
if (Math.abs(p1.calculate_distance(p2) - p1.calculate_distance(p3)) < 1e-15 && Math.abs(p2.calculate_distance(p1) - p2.calculate_distance(p3)) < 1e-15) {
shape = 1;
}
return shape;
}
//计算周长
public double calculateC() {
return p1.calculate_distance(p2) + p1.calculate_distance(p3) + p2.calculate_distance(p3);
}
//计算面积
public double calculateS() {
return Math.abs(p1.getX() * p2.getY() + p2.getX() * p3.getY() + p3.getX() * p1.getY()
- p1.getX() * p3.getY() - p2.getX() * p1.getY() - p3.getX() * p2.getY()) / 2;
}
//计算三角形重心
public Point zhongxin() {
Point p = new Point();
double dx = (p1.getX() + p2.getX() + p3.getX()) / 3;
double dy = (p1.getY() + p2.getY() + p3.getY()) / 3;
p.input(dx, dy);
return p;
}
//若是锐角三角形返回1,若是直角三角形返回0,若是钝角三角形则返回-1
public int shape_jiao_triangle() {
int shape;
double s1 = (p2.getX() - p1.getX()) * (p3.getX() - p1.getX())
+ (p2.getY() - p1.getY()) * (p3.getY() - p1.getY());
double s2 = (p3.getX() - p2.getX()) * (p1.getX() - p2.getX())
+ (p3.getY() - p2.getY()) * (p1.getY() - p2.getY());
double s3 = (p1.getX() - p3.getX()) * (p2.getX() - p3.getY())
+ (p1.getY() - p3.getY()) * (p2.getY() - p3.getY());
if (s1 < 0 || s2 < 0 || s3 < 0) {
shape = 1;
} else if (s1 == 0 || s2 == 0 || s3 == 0) {
shape = 0;
} else {
shape = -1;
}
return shape;
}
//计算直线与三角形的交点 返回交点个数
public int calculate_sum_jiaodian(Line a) {
int sum = 0;
Line l1 = new Line();
l1.p1 = p1;
l1.p2 = p2;
l1.zcline(l1);
Line l2 = new Line();
l2.p1 = p1;
l2.p2 = p3;
l2.zcline(l2);
Line l3 = new Line();
l3.p1 = p2;
l3.p2 = p3;
l3.zcline(l3);
if (l1.parallel(a) == 1) {
Point point1 = a.jiaodian(l2);
if (l2.if_in_line(point1)) {
sum++;
}
Point point2 = a.jiaodian(l3);
if (l3.if_in_line(point2)) {
sum++;
}
} else if (l2.parallel(a) == 1) {
Point point1 = a.jiaodian(l1);
if (l1.if_in_line(point1)) {
sum++;
}
Point point2 = a.jiaodian(l3);
if (l3.if_in_line(point2)) {
sum++;
}
} else if (l3.parallel(a) == 1) {
Point point1 = a.jiaodian(l1);
if (l1.if_in_line(point1)) {
sum++;
}
Point point2 = a.jiaodian(l2);
if (l2.if_in_line(point2) && !point1.check_point(point2)) {
sum++;
}
} else {
Point point1 = a.jiaodian(l1);
if (l1.if_in_line(point1)) {
sum++;
}
Point point2 = a.jiaodian(l2);
if (l2.if_in_line(point2) && !point1.check_point(point2)) {
sum++;
}
Point point3 = a.jiaodian(l3);
if (l3.if_in_line(point3) && !point1.check_point(point3) && !point2.check_point(point3)) {
sum++;
}
}
return sum;
}
//分割后三角形面积
public double fenge_triangleS(Line l) {
Line l1 = new Line();
Line l2 = new Line();
Line l3 = new Line();
Point p1 = new Point();
Point p2 = new Point();
Point p3 = new Point();
p1 = l.p1;
p2 = l.p2;
p3 = l.p3;
l1.p1 = p1;
l1.p2 = p2;
l2.p2 = p2;
l2.p3 = p3;
l3.p1 = p1;
l3.p3 = p3;
l1.zcline(l1);
l1.zcline(l2);
l1.zcline(l3);
double s = 0;
if (l.parallel(l1) != -1) {
p1 = l.jiaodian(l3);
p2 = l.jiaodian(l2);
l.p1 = p1;
l.p2 = p2;
s = l1.linedistance(this.p3) * p1.calculate_distance(p2) / 2;
if (s <= calculateS() / 2)
return s;
else
return calculateS() - s;
}
if (l.parallel(l3) != -1) {
p1 = l.jiaodian(l1);
p2 = l.jiaodian(l2);
l.p1 = p1;
l.p2 = p2;
s = l.linedistance(this.p1) * p1.calculate_distance(p2) / 2;
if (s <= calculateS() / 2)
return s;
else
return calculateS() - s;
}
if (l.parallel(l2) != -1) {
p1 = l.jiaodian(l3);
p2 = l.jiaodian(l1);
l.p1 = p1;
l.p2 = p2;
s = l.linedistance(this.p2) * p1.calculate_distance(p2) / 2;
if (s <= calculateS() / 2)
return s;
else
return calculateS() - s;
}
p1 = l.jiaodian(l1);
p2 = l.jiaodian(l3);
p3 = l.jiaodian(l2);
if (!l1.if_in_line(p1)) {
l.p2 = p2;
l.p3 = p3;
s = l.linedistance(this.p1) * p2.calculate_distance(p3) / 2;
}
if (!l3.if_in_line(p2)) {
l.p1 = p1;
l.p3 = p3;
s = l.linedistance(this.p2) * p1.calculate_distance(p3) / 2;
}
if (!l2.if_in_line(p3)) {
l.p1 = p1;
l.p2 = p2;
s = l.linedistance(this.p3) * p1.calculate_distance(p2) / 2;
}
if (s <= calculateS() / 2)
return s;
else
return calculateS() - s;
}
//判断是否在三角形内部
public boolean if_inside(Point p) {
Line a = new Line();
Line b = new Line();
Line c = new Line();
a.p1 = p1;
a.p2 = p2;
b.p1 = p2;
b.p2 = p3;
c.p1 = p3;
c.p2 = p1;
a.zcline(a);
b.zcline(b);
c.zcline(c);
double s1 = a.linedistance(p) * (a.p1).calculate_distance(a.p2) * 1 / 2;
double s2 = b.linedistance(p) * (b.p1).calculate_distance(b.p2) * 1 / 2;
double s3 = c.linedistance(p) * (c.p1).calculate_distance(c.p2) * 1 / 2;
if (Math.abs(s1 + s2 + s3 - calculateS()) < 1e-15)
return true;
else
return false;
}
}
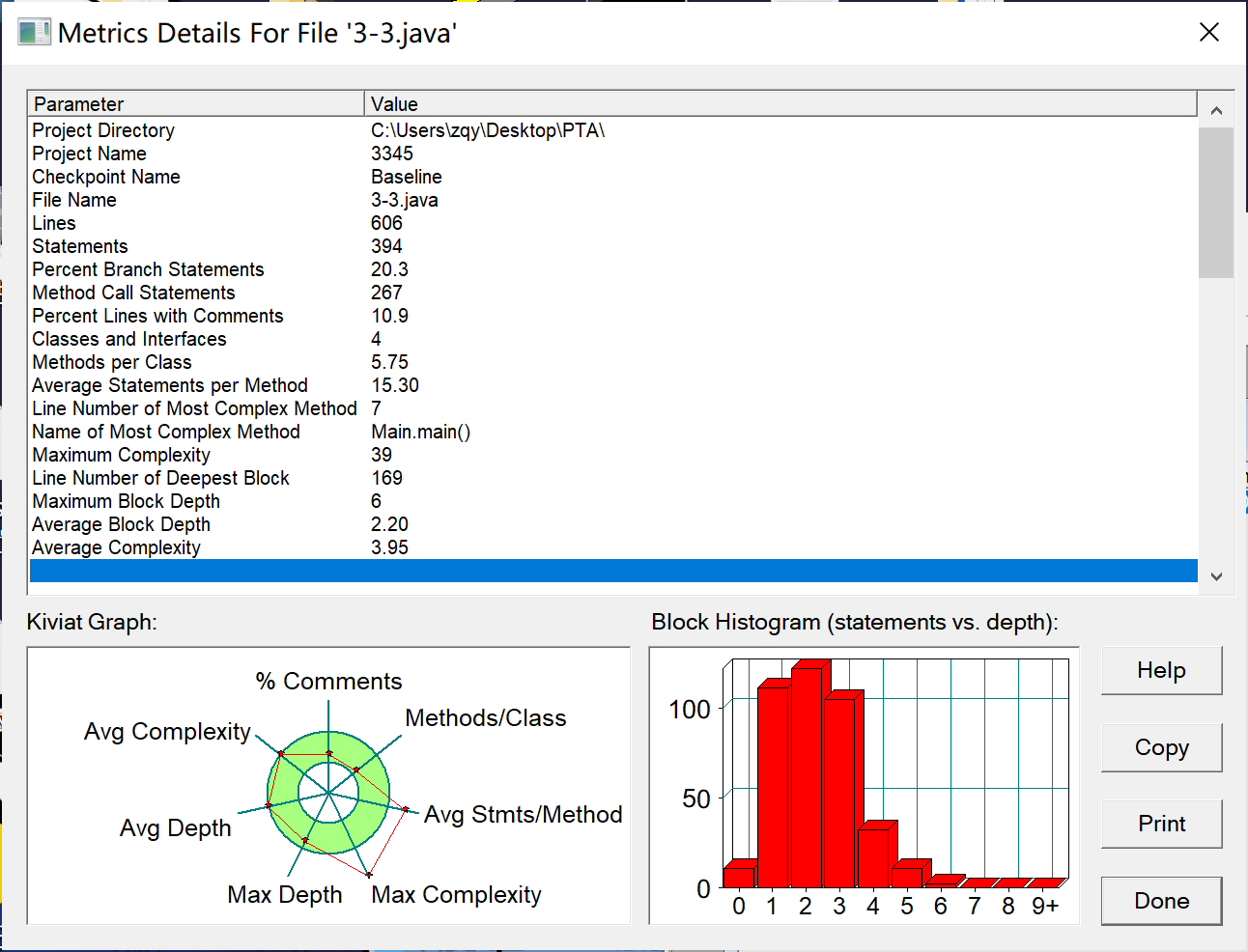
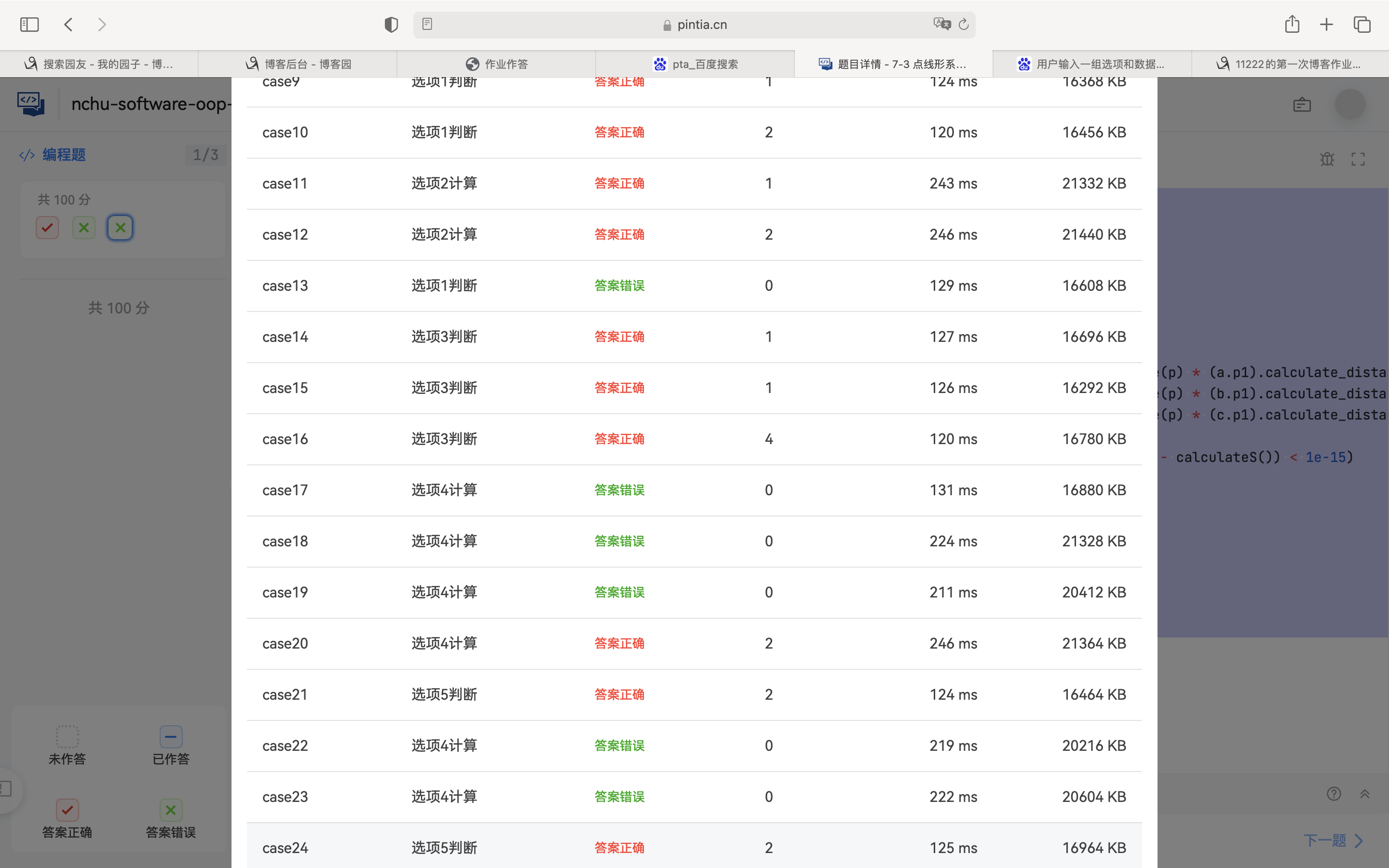
可以看到这题代码圈复杂度较高,以及最大复杂度,平均复杂度为3.95,也算良好。
踩坑心得:本次代码也没有满分,还没有足够的能力去过每一个测试点,就算测试样例都过也依旧有测试点错误,写类的时候还需要注意是私有变量还是公有变量,对类的对象定义时变量名也要注意,还有创造线对象时,不要忽略计算这个线具体的表达式,题目要求射线法,但是实在逻辑思维容易混乱,最终还是用了面积法。
改进建议:对if else语句的运用也要减少,提升自己的逻辑思维,多写注释,多动手操作,考虑多种情况,还要加强对类中属性和方法的定义使用,静态方法和动态方法的使用。
- 总结
这三次作业不仅是找回之前的语言知识,也是对java类的属性和方法的了解和初步掌握,在自己完成题目训练的过程中,不单单只考虑通过题目的测试,另一方面要去思考如何提高代码的可读性和简洁性,更好的展现知识成果。对老师上课讲的内容要及时实践温习,这样只有在做题时更加游刃有余。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号