CF1736B 1200 *

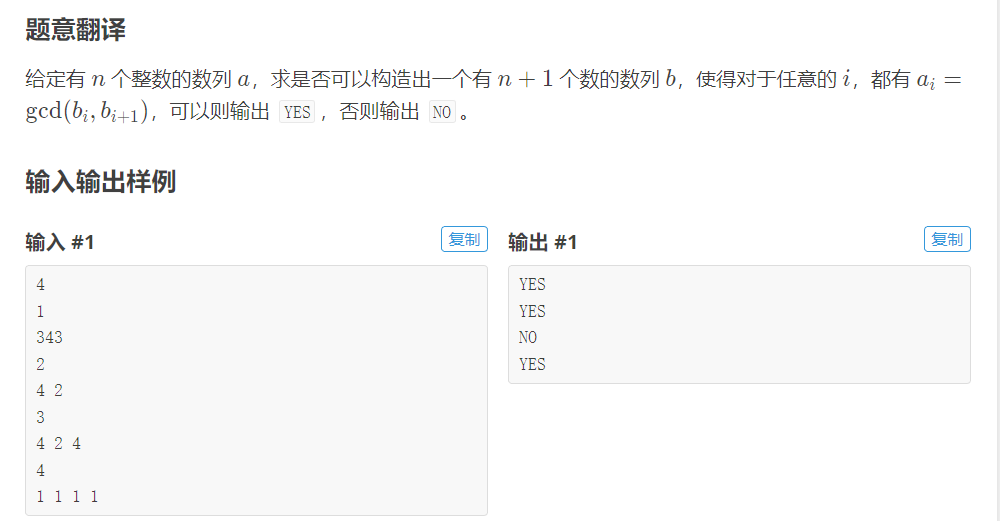
题意

解析

解析：每个a[i]是由b[i]和b[i+1]取最大公因数得出，所以对于每个b[j]来说应该既是a[j]的倍数，又是a[j-1]的倍数。现实在取的时候，可以取b[j] = lcm(a[j-1],a[j])。然后再对每个b[j]检查gcd(b[j],b[j+1])是否真的等于a[j]。
我们这样取保证了b[j]是a[j-1]和a[j]倍数。但不一定b[j]和b[j+1]的最大公因数是a[j]，因为有可能b[j]和b[j+1]多出了一个公共因子k，这样此时b[j]和b[j+1]的最大公因子就是k * a[j]了。所以要再检查一下。
这也是为什么我们取的时候取最小公倍数，这可以让其他因子尽可能的少。

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 2e5 + 10,M = 1e6 + 10;
int t,n,m,a[N],b[N],s[N],l;

bool check(){
    for(int i=1;i<=n;i++){
        if(__gcd(b[i],b[i+1]) != a[i]) return false;
    }
    return true;
}

int main(){
    scanf("%d",&t);
    while(t--){
        scanf("%d",&n);
        a[0] = 1;
        a[n+1] = 1;
        for(int i=1;i<=n;i++){
            scanf("%d",&a[i]);
        }
        for(int i=1;i<=n+1;i++){
            b[i] = a[i] * a[i-1] / __gcd(a[i],a[i-1]);
        }
        if(check()) puts("YES");
        else puts("NO");
    }
    return 0;
}