P3368 【模板】树状数组 2

【区间修改，单点查询】

题意

【模板】树状数组 2

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1. 将某区间每一个数加上 \(x\)；

2. 求出某一个数的值。

输入格式

第一行包含两个整数 \(N\)、\(M\)，分别表示该数列数字的个数和操作的总个数。

第二行包含 \(N\) 个用空格分隔的整数，其中第 \(i\) 个数字表示数列第 $i $ 项的初始值。

接下来 \(M\) 行每行包含 \(2\) 或 \(4\)个整数，表示一个操作，具体如下：

操作 \(1\)： 格式：1 x y k 含义：将区间 \([x,y]\) 内每个数加上 \(k\)；

操作 \(2\)： 格式：2 x 含义：输出第 \(x\) 个数的值。

输出格式

输出包含若干行整数，即为所有操作 \(2\) 的结果。

样例 #1

样例输入 #1

5 5
1 5 4 2 3
1 2 4 2
2 3
1 1 5 -1
1 3 5 7
2 4

样例输出 #1

6
10

提示

样例 1 解释：

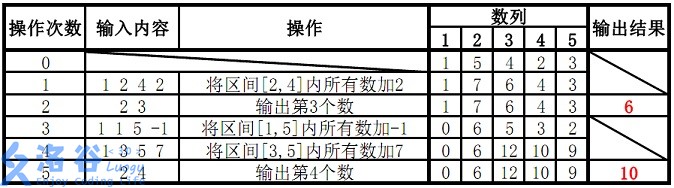
故输出结果为 6、10。

---

数据规模与约定

对于 \(30\%\) 的数据：\(N\le8\)，\(M\le10\)；

对于 \(70\%\) 的数据：\(N\le 10000\)，\(M\le10000\)；

对于 \(100\%\) 的数据：\(1 \leq N, M\le 500000\)，\(1 \leq x, y \leq n\)，保证任意时刻序列中任意元素的绝对值都不大于 \(2^{30}\)。

解析

区间修改，单点查询 模板题
实际还是单点修改，但只要对差分数组的两个端点修改，那就变成区间修改了
单点查询只要得到差分数组的前缀和就好了那就是单点的值
预处理O(nlogn) 查询修改O(nlogn)

这类题目如果范围不大，直接差分数组也能做。
但需要考虑复杂度，
差分预处理O(n) 查询一个点的复杂度O(n)
所以需要考虑查询的次数

代码

#include<bits/stdc++.h>
using namespace std;

const int N = 5e5 + 10;

int tr[N],n,m;

int lowbit(int x){
	return x & -x;
}

void add(int x,int k){
	while(x <= n){
		tr[x] += k;
		x = x + lowbit(x);
	}
}

int sum(int x){
	int ans = 0;
	while(x >= 1){
		ans += tr[x];
		x = x - lowbit(x);
	}
	return ans;
}

int main(){
	scanf("%d %d",&n,&m);

	for(int i=1,x;i<=n;i++){
		scanf("%d",&x);
		add(i,x);
		add(i+1,-x);
	}

	while(m--){
		int op,x,y,k;
		scanf("%d %d",&op,&x);
		if(op == 1){
			scanf("%d %d",&y,&k);
			add(x,k);
			add(y+1,-k);
		}else{
			printf("%d\n",sum(x));
		}
	}

	return 0;
}