bzoj1997 [HNOI2010]平面图判定Plana
bzoj1997 [HNOI2010]平面图判定Planar
链接
思路
好像有很多种方法过去。我只说2-sat
环上的边,要不在里面,要不在外边。
有的边是不能同时在里面的,可以O(m^2)的连边
但是m是10000,不过平面图内边数不得超过3*n-6,
m太大的直接NO就好了,其他的n,m是一个数量级的,直接2-sat暴力连边做就好了。
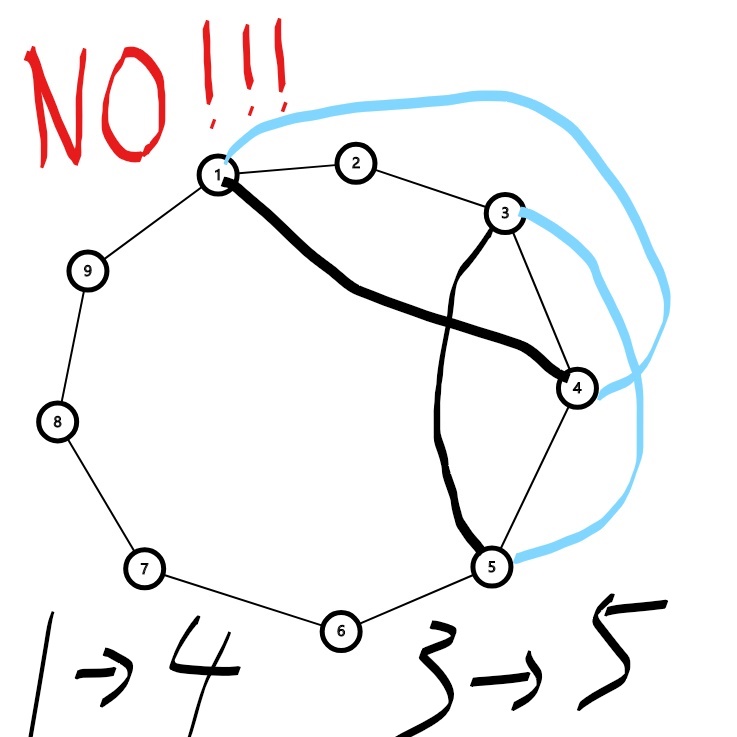
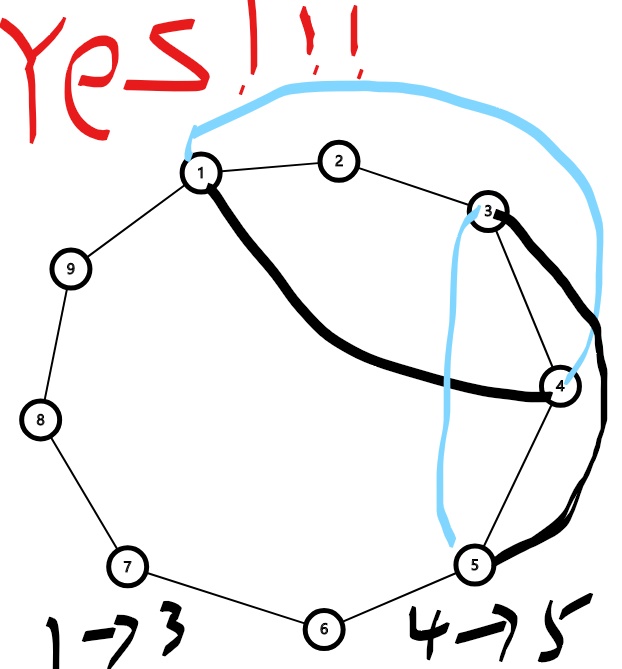
细节
双向边
是边m进行2-sat,不是点n
代码
#include <bits/stdc++.h>
using namespace std;
const int N=1207;
int read() {
int x=0,f=1;char s=getchar();
for(;s>'9'||s<'0';s=getchar()) if(s=='-') f=-1;
for(;s>='0'&&s<='9';s=getchar()) x=x*10+s-'0';
return x*f;
}
int n,m,a[N],u[10005],v[10005],tong[N],rk[10005];
struct node {int v,nxt;}e[N*N*2];
int head[N],tot;
map<pair<int,int >,int > Hash;
void add(int u,int v) {
e[++tot].v=v;
e[tot].nxt=head[u];
head[u]=tot;
}
int low[N],dfn[N],cnt,stak[N],top,vis[N],col,belong[N];
void tarjan(int u) {
dfn[u]=low[u]=++cnt;
vis[u]=1;
stak[++top]=u;
for(int i=head[u];i;i=e[i].nxt) {
int v=e[i].v;
if(!dfn[v]) {
tarjan(v);
low[u]=min(low[u],low[v]);
} else if(vis[v]) {
low[u]=min(low[u],dfn[v]);
}
}
if(low[u]==dfn[u]) {
++col;
while(stak[top]!=u) {
vis[stak[top]]=0;
belong[stak[top]]=col;
top--;
}
vis[u]=0;
belong[u]=col;
top--;
}
}
void clear() {
tot=cnt=col=0;
Hash.clear();
memset(head,0,sizeof(head));
memset(low,0,sizeof(low));
memset(dfn,0,sizeof(dfn));
memset(rk,0,sizeof(rk));
}
void solve() {
clear();
n=read(),m=read();
for(int i=1;i<=m;++i) u[i]=read(),v[i]=read();
for(int i=1;i<=n;++i) a[i]=read();
for(int i=2;i<=n;++i) {
rk[a[i]]=i;
Hash[make_pair(a[i],a[i-1])]=1;
Hash[make_pair(a[i-1],a[i])]=1;
}
Hash[make_pair(a[1],a[n])]=1;
Hash[make_pair(a[n],a[1])]=1;
if(m>3*n-6) return puts("NO"),void();
for(int i=1;i<=m;++i) {
if(!Hash[make_pair(u[i],v[i])]) {
memset(tong,0,sizeof(tong));
for(int j=1,flag=0;j<=n;++j) {
if(u[i]==a[j]||v[i]==a[j]) flag=flag^1;
tong[j]=flag;
}
for(int j=i+1;j<=m;++j) {
if(Hash[make_pair(u[j],v[j])]) continue;
if(u[i]==v[j]||u[i]==u[j]||v[i]==v[j]||v[i]==u[j]) continue;
if(tong[rk[u[j]]]^tong[rk[v[j]]]) {
add(i,j+m);
add(j+m,i);
add(i+m,j);
add(j,i+m);
}
}
}
}
for(int i=1;i<=2*m;++i)
if(!dfn[i])
tarjan(i);
for(int i=1;i<=m;++i)
if(belong[i]==belong[i+m])
return puts("NO"),void();
return puts("YES"),void();
}
int main() {
for(int T=read();T;T--) solve();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号