10.2 广州集训 Day1

平衡（balance,1s,128M）

【题目描述】

P同学总共有k根火柴，分别放在摆成一列的n个火柴盒内，保证k是n的倍数。P同学想要每个火柴盒都有相同数目的火柴，每次他可以从一个火柴盒中拿一根火柴放到相邻的火柴盒中。他想知道他最少要移动多少次。

【输入格式】

从balance.in中读入。

第一行一个整数n，表示火柴盒数。

第二行n个整数,表示第i个火柴盒内有根火柴。

【输出格式】

输出到balance.out中。

一行一个整数，表示最少要移动多少次。

【样例一输入】

6

1 6 2 5 3 7

【样例一输出】

12

【子任务】

30%数据，1≤n≤100,0≤𝑎𝑖≤100

100%数据，1≤n≤50000,0≤𝑎𝑖≤10^9

Solution：

　　模拟+贪心。

　　没有什么其他的特别的东西，类似于NOIP2002的纸牌。

　　我们可以先算出各盒火柴之和的sum，由p=sum/n可以得到每盒火柴的个数。

　　然后从1到n寻找，如果火柴数大于0，就把多出的火柴移到下一个火柴盒。

　　反之，如果小于0，就把下一个火柴盒的火柴移到这个火柴盒。

　　值得一提的是，即使火柴变成负数也可以实现，因为我们可以保证存在一种合适的移动方法恒为非负。

#include<cstdio>
#define MAXN 50005
#define LL long long
using namespace std;
int n,p=0;LL sum=0,cnt=0;
LL a[MAXN];
inline LL read(){
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
LL Abs(LL x){return x>0?x:-x;}
int main(){
    freopen("balance.in","r",stdin);
    freopen("balance.out","w",stdout);
    n=read();
    for(int i=1;i<=n;i++) a[i]=read(),sum+=a[i];
    p=sum/n;
    for(int i=1;i<=n;i++) a[i]-=p;
    //for(int i=1;i<=n;i++) printf("a[i]=%d\n",a[i]);
    for(int i=1;i<=n;i++) {
        if(!a[i]) continue;
        else if(a[i]<0) cnt-=a[i];
        else if(a[i]>0) cnt+=a[i];
        a[i+1]+=a[i];
    }
    printf("%lld",Abs(cnt));
    return 0;
}

 

 

　　

                                                    道路（road,3s,512M）

 

    我们看见了一个由m行n列的1*1的格子组成的矩阵，每个格子（I,j）有对应的高度h[i][j]和初始的一个非负权值v[i][j].我们可以随便选择一个格子作为起点，然后在接下来的每一步当中，我们能且只能到达与当前格子有边相邻的四个格子中的高度不超过当前格子高度的格子，每当我们到达一个新格子（包括一开始选择的初始格子），我们就能得到该格子的权值分，然后该格子的权值就会等概率变成不比当前的权值大的一个非负权值。每一个格子在满足前面条件情况下，可以走任意多次。
    我们希望得到一个最大的期望权值和路径，并给出这个最大的期望权值和。

输入格式：
    第一行两个正整数表示m，n。
    接下来的m行，每行n个正整数，表示h[i][j].
    接下来的m行，每行n个非负整数，表示v[i][j].

输出格式：
    一行一个实数，表示所求的最大期望权值和。保留零位小数。

输入样例：
    1 3
    1 2 1
    1 2 3

输出样例：
    5

数据范围：
    对于30%的数据，保证n,m不超过100.
    对于另外20%的数据，保证不存在相同的高度的格子。
    对于100%的数据，保证n,m不超过1000.所有权值与高度不超过10^9.

 Solution：

　　//留坑。下课填。

　　我们首先可以通过设一个概率的dp：f[i]表示原价值为i重复走无限多次的期望总价值。

　　然后可以得到以下式子：

　　

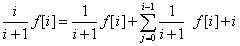
 　　化简可得：

　　　

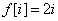
　　然后，我们就把连通的同高度点当成一个点，然后对剩余的DAG做一个dp去维护最大权路径就可以了。

　　//关于同一高度点的处理证明：相同高度点可以多次访问，即可以得到这一块的所有权值。权值非负可以得到贪心正确。

　　　　　　　　　　　　　　　　特判可以保证网络流不会死循环。

Other：

　　 关于数学期望：

　　 关于更新题解：

　　 //其实以上都是口胡，等A了之后再次更新

//std
#include <iostream>
#include <fstream>
#include <cstring>
#include <string>
#include <cstdlib>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <bitset>
#include <ctime>
#include <map>
#include <queue>
#include <set>
using namespace std;

const int maxn=1000+15;
const int dx[4]={-1,1,0,0};
const int dy[4]={0,0,-1,1};
vector <int> edge[maxn*maxn];
int belonging[maxn][maxn],sum;
long long keyvalue[maxn*maxn];
int m,n,height[maxn][maxn],value[maxn][maxn];
int lix[maxn*maxn],liy[maxn*maxn],hh,tt;
long long f[maxn*maxn],ans;
int bfs(int tx,int ty)
{
    lix[hh=tt=1]=tx;
    liy[hh]=ty;
    keyvalue[sum]+=value[lix[hh]][liy[hh]];
    belonging[lix[hh]][liy[hh]]=sum;
    for (;hh<=tt;hh++)
    {
     int x=lix[hh],y=liy[hh];
     for (int i=0;i<4;i++)
     {
         int nx=x+dx[i],ny=y+dy[i];
         if (nx==0 || nx>m || ny==0 || ny>n || height[nx][ny]!=height[x][y] || belonging[nx][ny]!=0) continue;
         tt++;
         lix[tt]=nx;
         liy[tt]=ny;
         keyvalue[sum]+=value[nx][ny];
         belonging[nx][ny]=sum;
     }
    }
    if (tt>1) keyvalue[sum]*=2;
    return 0;
}
int getint()
{
    char ch;
    for (ch=getchar();!isdigit(ch);ch=getchar());
    int s=0;
    for (;isdigit(ch);s=s*10+ch-'0',ch=getchar());
    return s;
}

long long dp(int x)
{
     if (f[x]!=-1) return f[x];
     f[x]=0;
     for (int j=0;j<edge[x].size();j++)
         f[x]=max(f[x],dp(edge[x][j]));
     f[x]+=keyvalue[x];
     return f[x];
}
int main()
{
    freopen("road.in","r",stdin);
    freopen("road.out","w",stdout);
    m=getint();n=getint();
    for (int i=1;i<=m;i++)
     for (int j=1;j<=n;j++)
      height[i][j]=getint();
    for (int i=1;i<=m;i++)
     for (int j=1;j<=n;j++)
      value[i][j]=getint();
    for (int i=1;i<=m;i++)
     for (int j=1;j<=n;j++)
      if (!belonging[i][j])
        {
            sum++;
            bfs(i,j);
        }
//    return 0;
//    int sss=0;
    for (int x=1;x<=m;x++)
     for (int y=1;y<=n;y++)
      for (int i=0;i<4;i++)
      {
          int nx=x+dx[i],ny=y+dy[i];
          if (nx==0 || nx>m || ny==0 || ny>n || height[nx][ny]>=height[x][y]) continue;
//          sss++;
          edge[belonging[x][y]].push_back(belonging[nx][ny]);
      }
///    cout << sss << endl;
    memset(f,-1,sizeof(f));
    for (int i=1;i<=sum;i++) ans=max(ans,dp(i));
    cout << ans << endl;
    return 0;
}

 

1 小豪的花园
程序文件名： flower.c/cpp/pas 输入文件： flower.in
输出文件： flower.out
时间限制： 3s
空间限制： 256Mb

 

题目描述
           小豪有一个花园，里面有n个花棚，编号1..n，每个花棚里有一定数量的花ai。小豪花园的路十分
神奇，可以使得任意两个花棚之间仅有一条最短路，即形成树结构，其中根节点是1号花棚。现在小豪 打算修缮一下他的花园，重新分配每个花棚里花的数量。为了能方便快捷地知道花园的情况，小豪现 在需要你的帮助。具体地说，小豪共有m个操作。操作有三种：
　　1. 1 u k 表示如果一个花棚在以u号花棚为根的子树中，那么小豪会把这个花棚花的数量模k
　　2. 2 u x 表示小豪将u号花棚花的数量变成x
　　3. 3 u v 表示小豪询问从u号花棚走到v号花棚总共能看到的花的数量
         你能帮助小豪吗？

输入格式
　　第一行有两个正整数n和m，代表花棚的数量和小豪操作的个数。
　　接下来n − 1行，每行两个正整数u, v(1 ≤ u, v ≤ n, u 6= v)，表示u号花棚与v号花棚直接有路相连。 下一行有n个非负整数a1, a2, ..., an，表示起始时每个花棚中花的数量。
　　接下来m行，一行表示一个操作，格式如题所述。（可参考样例）

 

输出格式
　　对于每个操作3输出一行一个整数表示结果。

 

样例

输入　　　　　　　　　　　　　　　　　　　　输出

8 7　　　　　　　　　　　　　　　　　　　　　12　
1 2 　　　　　　　　　　　　　　　　　　　　　20
2 3 　　　　　　　　　　　　　　　　　　　　　9
2 4
2 5
1 6
6 7
6 8
1 2 3 4 5 6 7 8
3 3 6 1 2 3 2 2 4 3 4 8 2 3 11
1 1 5 3 3 7

 

数据范围
　　• 对于20%的数据，n, m ≤ 2000
　　• 另外10%的数据，所有花棚构成一条链，且无操作1
　　• 另外20%的数据，无操作1
　　• 对于100%的数据，n, m ≤ 100000, ai, x, k ≤ 10^8, k ≥ 1

 

Solution：

　　这题是线段树（树状数组）、DFS序的综合应用。
　　首先对于50%的数据，就是裸的树链剖分。也有时间复杂度少一个log n的做法，见下文。
　　比较难搞的就是操作1，对子树取模，利用DFS序可以变成区间取模。
　　区间取模问题的做法很简单，就是不断找区间的最大值，一个一个地进行取模操作直至最大值小于要模的值。可以证明，这样 做操作1的总时间复杂度不超过O((n + m) log x + m log n) （x 表示花的数量的最大值，下同）。注意到 一个数模了另一个数后要么不变，要么至多变为原来的一半，如此一个数（若没有修改）最多只能变 化log x次，且修改总共最多m次，因此所有数被修改的总次数不超过(n + m) log x。这个结果加上查找 最大值的时间即可得上述时间复杂度O((n + m) log x + m log n)。
　　如此操作1和操作2都是单点修改，而操作3是路经询问。路经询问不好处理，可以通过差分变成子 树修改和单点询问。记f[u]表示u到根节点花的数量和，这样对于一个询问(u, v)，设w是u和v的最近公 共祖先，询问的答案就是f[u] + f[v] − 2 ∗ f[w] + a[w]；对于一个修改操作a[u] → x，则需要把u的子树 中所有f加上x − a[u]。利用DFS序，这两个操作用树状数组或者线段树即可完成。
　　上述做法时间复杂度O((n + m) log n log x + m log n)。若无上段所述的转化，直接用树链剖分，时 间复杂度是O((n + m) log2 n log x + m log n)，可能会超时。

 

Other：

　　实际上树剖是可以过的，只是操作一写挂的我树剖只有20分...

//std
#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <ctime>
#include <cmath>
#include <vector>
#include <iterator>
using namespace std;
typedef long long LL;

const int maxn = 100005;

int n, m, a[maxn];
int q[maxn], fa[maxn], dep[maxn], size[maxn], st[maxn], ed[maxn], index[maxn];
int Bits, lca[maxn][20];
vector<int> edge[maxn];

void Bfs(int root)
{
    int h = 0, t = 0;
    fa[root] = 0; q[0] = root; dep[root] = 1;
    for (; h <= t; h++)
    {
        int u = q[h];
        for (int i = edge[u].size()-1; i >= 0; i--)
        // for (vector<int>::iterator i = edge[u].begin(); i != edge[u].end(); ++i)
        {
            // int v = *i;
            int v = edge[u][i];
            if (fa[u] == v) continue;
            q[++t] = v;
            fa[v] = u;
            dep[v] = dep[u] + 1;
        }
    }
    for (h = t; h >= 0; h--)
    {
        int u = q[h];
        size[u] = 1;
        for (int i = edge[u].size()-1; i >= 0; i--)
        // for (vector<int>::iterator i = edge[u].begin(); i != edge[u].end(); ++i)
        {
            // int v = *i;
            int v = edge[u][i];
            if (fa[u] == v) continue;
            size[u] += size[v];
        }
    }
    st[root] = 1; ed[root] = n;
    for (h = 0; h <= t; h++)
    {
        int u = q[h], t = st[u] + 1;
        for (int i = edge[u].size()-1; i >= 0; i--)
        // for (vector<int>::iterator i = edge[u].begin(); i != edge[u].end(); ++i)
        {
            // int v = *i;
            int v = edge[u][i];
            if (fa[u] == v) continue;
            st[v] = t;
            t += size[v];
            ed[v] = t - 1;
        }
    }
    for (int i = 1; i <= n; i++)
        index[ st[i] ] = i;
}

void LcaInit()
{
    for (Bits = 0; (1 << (Bits + 1)) <= n; Bits++);
    for (int i = 1; i <= n; i++)
        lca[i][0] = fa[i];
    for (int j = 1; j <= Bits; j++)
        for (int i = 1; i <= n; i++)
            if (lca[i][j-1]) lca[i][j] = lca[ lca[i][j-1] ][j-1];
}

int Lca(int u, int v)
{
    if (dep[v] > dep[u]) swap(u, v);
    for (int i = Bits; i >= 0; i--)
        if (dep[ lca[u][i] ] >= dep[v])
            u = lca[u][i];
    if (u == v) return u;
    for (int i = Bits; i >= 0; i--)
        if (lca[u][i] != lca[v][i])
            u = lca[u][i], v = lca[v][i];
    return fa[u];
}

namespace SegTreeMax
{
    #define lson (root << 1)
    #define rson (root << 1 | 1)

    int tree[4*maxn], id[4*maxn];

    void Update(int root, int l, int r, int x, int val)
    {
        if (x < l || x > r) return;
        if (l == x && r == x)
        {
            tree[root] = val;
            id[root] = l;
            return;
        }
        int mid = (l + r) >> 1;
        Update(lson, l, mid, x, val);
        Update(rson, mid+1, r, x, val);
        if (tree[lson] > tree[rson])
        {
            tree[root] = tree[lson];
            id[root] = id[lson];
        } else {
            tree[root] = tree[rson];
            id[root] = id[rson];
        }
    }

    int Query(int root, int l, int r, int x, int y, int val)
    {
        if (y < l || x > r || tree[root] < val) return -1;
        if (x <= l && r <= y) return id[root];
        int mid = (l + r) >> 1;
        int ret = Query(lson, l, mid, x, y, val);
        if (ret != -1) return ret;
        return Query(rson, mid+1, r, x, y, val);
    }
}

namespace TreeArray
{
    LL tree[maxn];

    void Update(int x, int y, int val)
    {
        for (; x <= n; x += x & -x)
            tree[x] += val;
        for (y++; y <= n; y += y & -y)
            tree[y] -= val;
    }

    LL Query(int x)
    {
        LL sum = 0;
        for (; x; x -= x & -x)
            sum += tree[x];
        return sum;
    }
}

int main()
{
    freopen("flower.in", "r", stdin);
    freopen("flower.out", "w", stdout);

    scanf("%d%d", &n, &m);
    for (int i = 1; i < n; i++)
    {
        int u, v;
        scanf("%d%d", &u, &v);
        edge[u].push_back(v);
        edge[v].push_back(u);
        // Insert(u, v);
    }
    Bfs(1);
    LcaInit();

    for (int i = 1; i <= n; i++)
    {
        int x;
        scanf("%d", &x);
        a[i] = x;
        TreeArray::Update(st[i], ed[i], x);
        SegTreeMax::Update(1, 1, n, st[i], x);
    }
    for (int i = 1; i <= m; i++)
    {
        int t, u, v, x;
        scanf("%d", &t);
        if (t == 1)
        {
            scanf("%d%d", &u, &x);
            // cerr << x << endl;
            while ((v = SegTreeMax::Query(1, 1, n, st[u], ed[u], x)) != -1)
            {
                // cerr << v << endl;
                v = index[v];
                // cerr << v << endl;
                TreeArray::Update(st[v], ed[v], a[v] % x - a[v]);
                a[v] %= x;
                SegTreeMax::Update(1, 1, n, st[v], a[v]);
            }
        }
        else if (t == 2)
        {
            scanf("%d%d", &v, &x);
            TreeArray::Update(st[v], ed[v], x - a[v]);
            a[v] = x;
            SegTreeMax::Update(1, 1, n, st[v], a[v]);
        }
        else {
            scanf("%d%d", &u, &v);
            x = Lca(u, v);
            LL uSum = TreeArray::Query(st[u]);
            LL vSum = TreeArray::Query(st[v]);
            LL xSum = TreeArray::Query(st[x]);
            // cerr << u << ' ' << v << ' ' << x << endl;
            // cerr << uSum << ' ' << vSum << ' ' << xSum << endl;
            // cerr << a[x] << endl;
            printf("%I64d\n", uSum + vSum - 2 * xSum + a[x]);
        }
    }
}