算法

Python 算法
时间复杂度，用来评估算法运行效率的一个东西

print("Hello World") O(1)

for i in range(n):
print("Hello World") O(n)

for i in range(n):
for j in range(n):
print("Hello World") O(n^2)

for i in range(n)
for j in range(n):
for k in range(n):
print("Hello World") O(n^3)

while n>1:
print(n)
n=n//2 O(logn)

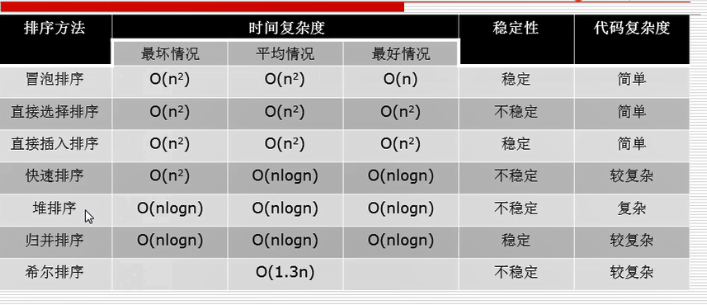
时间复杂度按效率排序
O(1)<O(logn)<O(n)<O(nlogn)<O(n^2)<O(n^2logn)<O(n^3)

如何一眼判断时间复杂度
循环减半的过程---O(logn)
几次循环就是n的几次放的复杂度

空间复杂度用来评估算法内存占用大小的一个式子

排序lowB三人组：
冒泡、选择、插入
快排
排序NB二人组
堆排序、归并排序
几乎没人用的排序
基数排序、希尔排序、桶排序

 

 

 

冒泡排序
两层for循环，第一层n-1,第二次n-i-1,时间复杂度O(n^2)

 

#!/usr/bin/env python
# _*_coding:utf-8_*_
# __author__="lihongxing"
import random,time

# 二分查找
def bin_search(set_data,val):
    low = 0
    high = len(set_data)-1
    while low<=high:
        mid = (low+high)//2
        if set_data[mid] == val:
            return mid
        elif set_data[mid] <val:
            low = mid +1
        else:
            high = mid -1
    return mid
bin_search([1,2,3,4,5,6,7,8,9],8)


# 冒泡排序
def bsort(list_data):
    now = time.time()
    for j in range(len(list_data)-1):
        exchange = False
        for i in range(len(list_data)-1-j):
            if list_data[i] < list_data[i+1]:
                list_data[i],list_data[i+1] = list_data[i+1],list_data[i]
                exchange = True
        if not exchange:
            break
    end = time.time()
    print(int(end)-int(now))
data = range(5000)
random.shuffle(data)
bsort(data)

　　

#选择排序
def select_sort(li):
    for i in range(len(li)-1):
        min_loc = i
        for j in range(i+1,len(li)):
            if li[j] < li[min_loc]:
                min_loc = j
        li[i],li[min_loc] = li[min_loc],li[i]
    print(li)
select_data = range(100)
random.shuffle(select_data)
select_sort(select_data)



# 插入排序
def insert_sort(li):
    for i in range(1,len(li)):
        tmp = li[i]
        j = i -1
        while j >= 0 and li[j] >tmp:
            li[j+1] = li[j]
            j -= 1
        li[j+1] = tmp
    print(li)
insert_data = range(100)
random.shuffle(insert_data)
insert_sort(insert_data)

　　

快排

取一个元素p（第一个元素）随便取，使元素P归位；

列表被P分成两部分，左边都比P小，右边都比P大

递归完成排序

排序前：[5,7,4,6,3,1,2,9,8]

P归位：[2,1,4,3,5,6,7,9,8]

目标：[1,2,3,4,5,6,7,8,9]

大框架

def quick_sort(data,left,right):
    if left < right:
        mid = partition(data,left,right)
        quick_sort(data,left,mid - 1)
        quick_sort(data,left,mid + 1,right)

　　

具体代码

# 快排
def quick_sort(data,left,right):
    if left < right :
        mid = partition(data,left,right)
        quick_sort(data,left,mid-1)
        quick_sort(data,mid+1,right)
def partition(data,left,right):
    tmp = data[left]
    while left < right:
        while left < right and data[right] >= tmp: #左和右不想等，没有碰，并且右边的值大于随机取出的值，减一不动，右边永远比P值大
            right -= 1
        data[left] = data[right]                   #右边的某个值，没有P大的时候，把右边的这个值，放到最左边left处
        while left < right and data[left] <= tmp:  #右边开始有空缺，从左开始判断，让左边的都小于P值，如果小，左边永远比P小，+1不动
            left += 1
        data[right] = data[left]                   #左边某个值比P大，就把左边的扔到右边
    data[left] = tmp #中间mid值，left和right都行
    return left     #返回中间mid值，同上
quick_data = range(100)
random.shuffle(quick_data)
quick_sort(quick_data,0,len(quick_data)-1)

　　

 

堆排序

https://www.cnblogs.com/shiqi17/p/9694938.html

堆排序过程
1：建立堆
2：得到堆顶元素，为最大元素
3：去掉堆顶，将堆最后一个元素放到堆顶，此时可通过一次调整重新使堆有序
4：堆顶元素为第二大元素
5：重复步骤3，直到堆变空

def sift(data, low, high):
    i = low      # 父节点
    j = 2 * i + 1   # 左子节点
    tmp = data[i]   # 父节点值
    while j <= high:    # 子节点在节点中
        if j < high and data[j] > data[j + 1]:  # 有子节点且左节点比右节点值大
            j += 1
        if tmp > data[j]:
            data[i] = data[j]   # 将父节点替换成新的子节点的值
            i = j   # 变成新的父节点
            j = 2 * i + 1   # 新的子节点
        else:
            break
    data[i] = tmp   # 将替换的父节点值赋给最终的父节点


def heap_sort(data):
    n = len(data)
    # 创建堆
    for i in range(n//2-1, -1, -1):
        sift(data, i, n-1)

    # 挨个出数
    for i in range(n-1, -1, -1):    # 从大到小
        data[0], data[i] = data[i], data[0]     # 将最后一个值与父节点交互位置
        sift(data, 0, i-1)


li = list(range(10))
random.shuffle(li)
print(li)
heap_sort(li)
print(li)

　　

归并排序

https://www.cnblogs.com/shiqi17/p/9696301.html

先分开再合并，分开成单个元素，合并的时候按照正确顺序合并

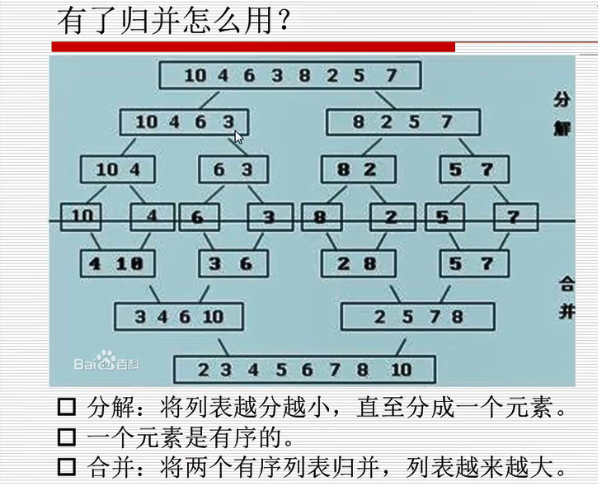
#归并排序
def merge(li, low, mid, high):
    i = low
    j = mid +1
    ltmp = []
    while i <= mid and j <= high:  #两边都有数
        if li[i] <=li[j]:           #左边没有右边大
            ltmp.append(li[i])      #左边的放到新列表内
            i += 1                  #下标+1 往左移一个继续比较
        else:
            ltmp.append(li[j])      #右边没左边大，同上
            j += 1
    while i <= mid:                 #右边的数被拿完了，只有左边还有
        ltmp.append(li[i])          #左边的数+1一个一个全部拿到新列表
        i += 1
    while j <= high:                #左边的被拿完了，只有右边有数，同上
        ltmp.append(li[j])
        j += 1
    li[low:high+1] = ltmp            #把新列表的数，赋给最初的li旧列表
def mergesort(li, low, high):
    if low < high:   #递归当low和high相同时，即分解到最后只剩一个的时候，停止递归
        mid = (low + high) //2
        mergesort(li, low, mid)  #左边分解
        mergesort(li, mid+1, high) #右边分解
        merge(li, low, mid, high)   #一次归并，分解是从列表多到一个分解，合并是从一个到多个合并，递归的性质就这样
merge_data = range(100)
random.shuffle(merge_data)
mergesort(merge_data,0,len(merge_data)-1)
print("merge_data:",merge_data)