BitMap的原理以及运用

  

位图（Bitmap），即位（Bit）的集合，是一种数据结构，可用于记录大量的0-1状态，在很多地方都会用到，比如Linux内核（如inode，磁盘块）、Bloom Filter算法等，其优势是可以在一个非常高的空间利用率下保存大量0-1状态。

 

BitMap的原理

  BitMap 的基本原理就是用一个bit 位来存放某种状态，适用于大规模数据，但数据状态又不是很多的情况。通常是用来判断某个数据存不存在的。

  举例：在Java里面一个int类型占4个字节，假如要对于10亿个int数据进行处理呢？10亿*4/1024/1024/1024=4个G左右，需要4个G的内存。  

            如果能够采用bit储,10_0000_0000Bit=1_2500_0000byte=122070KB=119MB, 那么在存储空间方面可以大大节省。

  在Java里面，BitMap已经有对应实现的数据结构类java.util.BitSet，BitSet的底层使用的是long类型的数组来存储元素。

  我们来看看具体存储：

  对于1，3，5，7这四个数，如果存在的话，则可以这样表示：

  

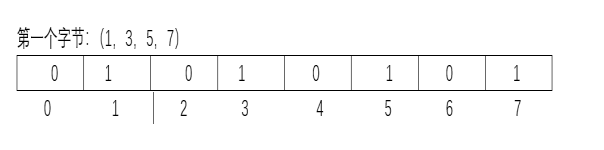
  1代表这个数存在，0代表不存在。例如表中01010101代表1，3，5，7存在，0，2，4，6不存在。那如果8，10，14也存在怎么存呢？如图，8，10，14我们可以存在第二个字节里

    

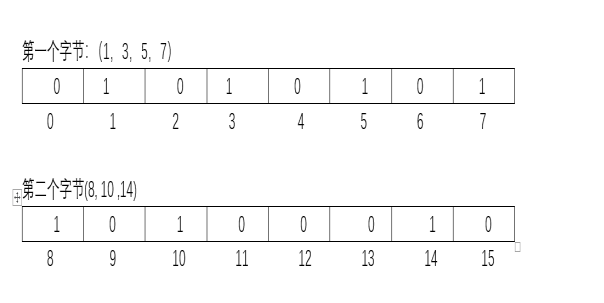
   以此类推。

Map映射表

    假设需要排序或者查找的总数N=10000000，那么我们需要申请内存空间的大小为int a[1 + N/32]，其中：a[0]在内存中占32为可以对应十进制数0-31，依次类推： 
    bitmap表为： 
   a[0]--------->0-31 
   a[1]--------->32-63 
   a[2]--------->64-95 
   a[3]--------->96-127 
   .......... 

BitMap算法处理大数据问题的场景：

 （1）给定10亿个不重复的正int的整数，没排过序的，然后再给一个数，如何快速判断这个数是否在那10亿个数当中。

解法：遍历40个亿数字，映射到BitMap中，然后对于给出的数，直接判断指定的位上存在不存在即可。

 （2）使用位图法判断正整形数组是否存在重复

解法：遍历一遍，存在之后设置成1，每次放之前先判断是否存在，如果存在，就代表该元素重复。

 （3）使用位图法进行元素不重复的正整形数组排序

解法：遍历一遍，设置状态1，然后再次遍历，对状态等于1的进行输出，参考计数排序的原理。

 （4）在2.5亿个整数中找出不重复的正整数，注，内存不足以容纳这2.5亿个整数

解法1：采用2-Bitmap（每个数分配2bit，00表示不存在，01表示出现一次，10表示多次，11无意义）。

解法2：采用两个BitMap，即第一个Bitmap存储的是整数是否出现，接着，在之后的遍历先判断第一个BitMap里面是否出现过，如果出现就设置第二个BitMap对应的位置也为1，最后遍历BitMap，仅仅在一个BitMap中出现过的元素，就是不重复的整数。

解法3：分治+Hash取模，拆分成多个小文件，然后一个个文件读取，直到内存装的下，然后采用Hash+Count的方式判断即可。

该类问题的变形问题，如已知某个文件内包含一些电话号码，每个号码为8位数字，统计不同号码的个数。8位最多99 999 999，大概需要99m个bit，大概10几m字节的内存即可。 （可以理解为从0-99 999 999的数字，每个数字对应一个Bit位，所以只需要99M个Bit==12MBytes，这样，就用了小小的12M左右的内存表示了所有的8位数的电话）

BitMap的一些缺点：

（1）数据碰撞。比如将字符串映射到 BitMap 的时候会有碰撞的问题，那就可以考虑用 Bloom Filter 来解决，Bloom Filter 使用多个 Hash 函数来减少冲突的概率。

（2）数据稀疏。又比如要存入(10,8887983,93452134)这三个数据，我们需要建立一个 99999999 长度的 BitMap ，但是实际上只存了3个数据，这时候就有很大的空间浪费，碰到这种问题的话，可以通过引入 Roaring BitMap 来解决。

例子：

   从正整数数组中寻找重复的整数

  

import java.util.BitSet;
import java.util.HashSet;
import java.util.Set;

public class TestBitMap {
        //假设数据是以数组的形式给我们的
        public static Set test(int[] arr) {
            int j = 0;
            //避免返回重复的数，存在Set里
            Set output = new HashSet();
            BitSet bitSet = new BitSet(Integer.MAX_VALUE);
            int i = 0;
            while (i < arr.length) {
                int value = arr[i];
                //判断该数是否存在bitSet里
                if (bitSet.get(value)) {
                    output.add(value);
                } else {
                    bitSet.set(value, true);
                }
                i++;
            }
            return output;
        }
        //测试
        public static void main(String[] args) {
            int[] t = {1,2,3,4,5,6,7,8,3,4,9};
            Set t2 = test(t);
            System.out.println(t2);
        }
    }

 

总结

     本文主要介绍了BitMap算法的基本原理和应用案例，其本质上是采用了bit位来表示元素状态，从而在特定场景下能够极大的节省存储空间，非常适合对海量数据的查找，判重，删除等问题的处理。

其他参考：

https://www.cnblogs.com/hongdada/p/8267032.html

https://www.cnblogs.com/gczr/p/7358813.html