数论热血实战

1.

题目：https://vjudge.net/contest/316798#problem/P

codes:

#include<iostream>
#include<cmath>
#include<algorithm>
int s[1000005];

using namespace std;
int main()
{
	int m,k;//欲求第k个与m互质的整数   kth  GCD(s[k] ,m)==1 
	while(cin>>m>>k)
	{
		int i;
		int num=0;
		for(i=1;i<=m;i++)
		{
			if(__gcd(m,i)==1) s[num++]=i; //num是小于m且与m互质的正整数的个数 
		}
		if(k%num==0) cout<<(k/num-1)*m+s[num-1]<<endl;// s[num-1],m+s[num-1],2m+s[num-1],.... 
		else cout<<k/num*m+s[k%num-1]<<endl;// 不妨令k<num,s[k-1],m+s[k-1],2m+s[k-1],... 
	}
	return 0;
}

参考：https://blog.csdn.net/huangshuai147/article/details/51277645

 

2.

题目：https://vjudge.net/contest/316798#problem/A

pre:

前进前之热身：

#include<iostream>
using namespace std;
int exgcd(int a,int b,int& x,int& y)//该用引用之处还是要用引用样子呀！ 
{
	if(b==0)
	{
		x=1;
		y=0;
		return a;
	}
	int t=exgcd(b,a%b,x,y);//training!!
	int x0=x;
	int y0=y;
	x=y0;
	y=x0-(a/b)*y0;
	return t;
} 
int main()
{
	int a,b,x,y,t;
	cin>>a>>b;
	t=exgcd(a,b,x,y);
	cout<<t<<endl;
	cout<<x<<" "<<y<<endl;
	return 0;
}

解决方案可见于我的另一篇博客：《数论：扩展欧几里得》

3.

题目：https://vjudge.net/contest/316798#problem/B

 

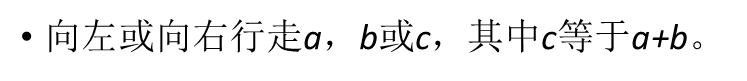
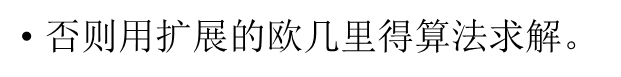
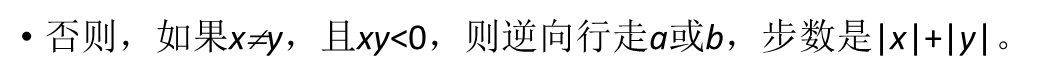
Repeat:

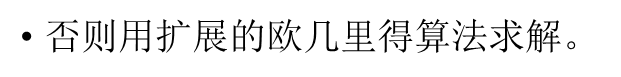
在c是GCD(a,b)的倍数的情况下：

 //左边之系数与右边放置之数具去同除！

...............

 

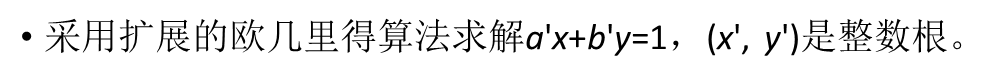
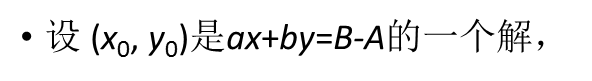
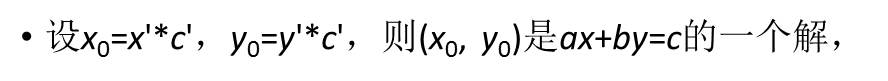codes:

 

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int exgcd(ll a,ll b,ll& x,ll& y)
{
	if(b==0)
	{
		x=1;
		y=0;
		return a;
	}
	ll t=exgcd(b,a%b,x,y);
	ll x0=x;
	ll y0=y;
	x=y0;
	y=x0-(a/b)*y0;
	return t;
}
int main()
{
	int t;
	cin>>t;
	while(t--)
	{
		ll c,d,a,b,x,y,x0,y0;//c为起点，d为终点;步长:a,b;
		cin>>c>>d>>a>>b;
		
		if(c>d) swap(c,d);
		ll u=d-c;//距离
		 
		ll g=exgcd(a,b,x,y);//g=GCD(a,b),默认的那一组解所对应的方程右侧之值是为1! 
		if(u%g!=0) 
		{
			cout<<-1<<endl;
			continue;
		}//从头再来 
		else
		{
			a/=g;
			b/=g;
			x*=(u/g);
			y*=(u/g);
			
			ll k=(y-x)/(a+b);
			ll ans=1e18;
			for(int i=k-1;i<=k+1;i++)
			{
				x0=x+i*b;
				y0=y-i*a;
				if(abs(x0)+abs(y0)==abs(x0+y0)) ans=min(ans,max(x0,y0));
				else ans=min(ans,abs(x0)+abs(y0));
			}
			cout<<ans<<endl;
		}
	}
	return 0;
}



	/*	int t=__gcd(a,b);
		a/=t;b/=t;d/=t;
		exgcd(a,b,x,y);
		x=d*x;
		y=d*y;    */