OpenGLshader开发实战学习笔记：第一章初识游戏图形

参考资料

1. 1.初识游戏图形

1.1. 什么是渲染

渲染的本质是创建2D图像的过程，即将一堆数据（如2D或3D网格，以及灯光、游戏摄像机等）创建为图像，渲染过程通常由GPU完成。对于游戏来讲，渲染过程是一个持续的过程，需要以每秒30帧-120帧的速度进行渲染，这样才能保证游戏画面的流畅性。游戏中很重要的一个指标是帧率，帧率越高，游戏画面越流畅，帧率越低，游戏画面越卡顿。

1.1.1. 什么是游戏引擎

游戏引擎是一个软件框架，它提供了一组工具和库，用于开发游戏。游戏引擎通常包含以下组件：

渲染引擎：用于创建2D或3D图像的引擎。用于将网格数据转换为新帧的一系列步骤称为渲染管线。
游戏逻辑引擎：用于处理游戏逻辑的引擎。
资源管理引擎：用于管理游戏资源的引擎。
物理引擎：用于模拟物理效果的引擎。
音频引擎：用于处理音频的引擎。
人工智能引擎：用于处理人工智能的引擎。
网络引擎：用于处理网络通信的引擎。
编辑器：用于编辑游戏的工具。

1.2. 网格是什么

网格的不同成分的示例：从左到右是顶点、边、面网格是游戏图形中最重要的概念之一，它是由顶点、边和面组成的数据结构。顶点是网格的点，边是连接两个顶点的线段，面是三个或更多顶点组成的多边形。网格可以由三角形、四边形、五边形等组成。

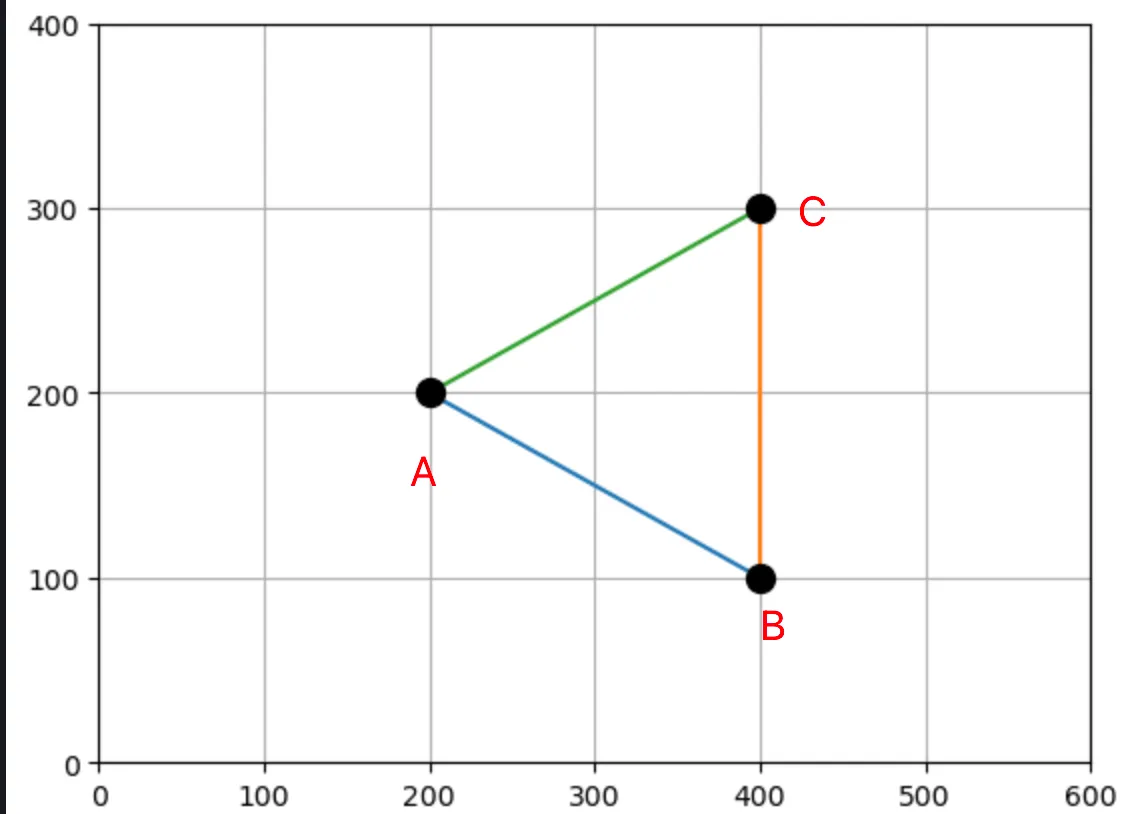
顶点的顺序很重要，因为它用于确定面的方向。即哪一面为“正面”。有的选择顺时针为正面(A,C,B)，有的选择逆时针为正面(A,B,C) 游戏通常不会渲染网格的背面，因为它是不可见的，这是一种称为背面剔除的技术。网格中的顶点使用向量表示

1.3. 向量入门

向量是游戏图形中最重要的概念之一，它是由起点和终点组成的线段。向量可以表示方向、速度、加速度等。向量可以表示方向，例如一个人在向右移动，那么他的方向就是向右。向量可以表示速度，例如一个人在向右移动，那么他的速度就是向右的速度。向量本身不表示位置，而是表示方向和大小。

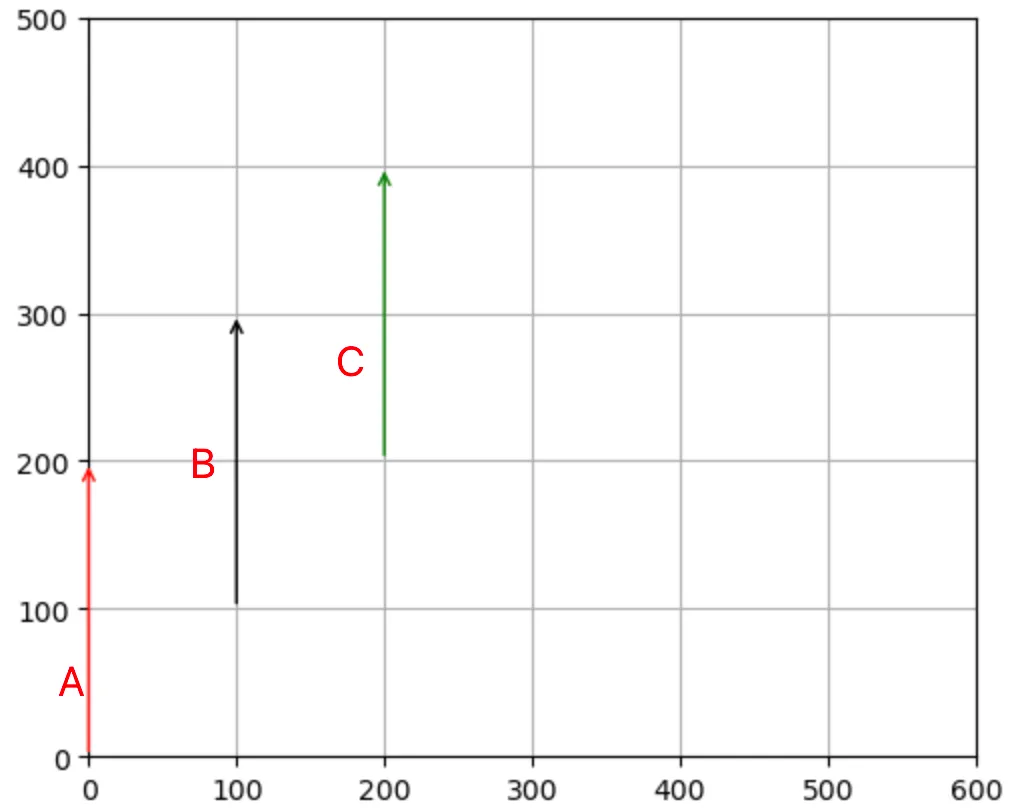
图中向量A 、向量B、向量C 是一样的。针对这三个向量，都可以用(0,200)表示，即从(0,0)到(0,200)。即二维空间，用(x,y)表示。三维空间，用(x,y,z)表示。四维空间，用(x,y,z,w)表示。在着色器代码中，通常使用vec2、vec3、vec4来表示向量。

1.3.1. 单位向量

单位向量是一个长度为1的向量，它的方向与原向量相同。

将非单位向量转换为单位向量的过程称为归一化(normalization),通过将向量的每个分量除以向量的长度，即可得到单位向量。

1.3.2. 向量加法

向量加法是两个向量的和，即起点和终点相加。例如，向量A = (4,1)，向量B = (0,3)，那么向量C=A + B = (4+0,1+3)=(4,4)。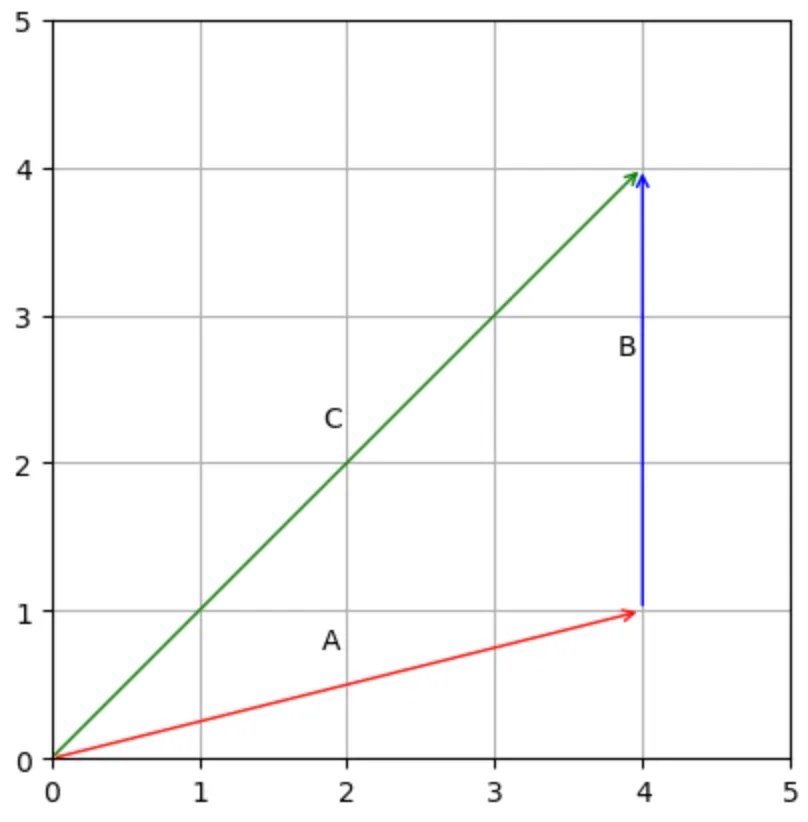

1.3.3. 向量减法

向量减法是两个向量之间的运算，其结果是一个新的向量。具体来说，如果存在两个向量 $\mathbf{A}$ 和 $\mathbf{B}$ ，则它们的差（即 $\mathbf{A} - \mathbf{B}$ ）也是一个向量，这个向量表示从 $\mathbf{B}$ 的终点指向 $\mathbf{A}$ 的终点的方向和大小。

在二维或三维空间中，如果 $\mathbf{A} = (a_1, a_2)$ 或且 $\mathbf{B} = (b_1, b_2)$ 或，那么向量减法可以按照分量来计算：

$\mathbf{A} - \mathbf{B} = (a_1 - b_1, a_2 - b_2) \\$

或者对于三维情况：

$\mathbf{A} - \mathbf{B} = (a_1 - b_1, a_2 - b_2, a_3 - b_3) \\$

这意味着，对于每一对对应的坐标，我们都执行减法操作。例如，在二维空间中，如果你有向量 $\mathbf{A} = (4, 5)$ 和 $\mathbf{B} = (2, 3)$ ，那么它们的差为：

$\mathbf{A} - \mathbf{B} = (4 - 2, 5 - 3) = (2, 2) \\$

几何上，你可以将向量减法理解为连接向量 $\mathbf{B}$ 的终点到向量 $\mathbf{A}$ 的终点所形成的向量。这可以通过平移向量实现，使得它们共享相同的起点，然后画一个从 $\mathbf{B}$ 的终点到 $\mathbf{A}$ 的终点的箭头来直观地表示这个结果向量。

向量减法在物理学、工程学、计算机图形学等领域有着广泛的应用，用于计算位移、速度、加速度等物理量的变化，或者是在空间中进行导航和定位。

1.3.4 向量与标量相乘

向量与标量相乘是向量的长度乘以一个标量。

$\mathbf{A} = (A_x, A_y), \quad k \in \mathbb{R}, \quad \mathbf{C} = k \cdot \mathbf{A} = (k \cdot A_x, k \cdot A_y) \\$ $\text{例如：} \quad \mathbf{A} = (4, 1), \quad k = 2, \quad \mathbf{C} = k \cdot \mathbf{A} = (2 \cdot 4, 2 \cdot 1) = (8, 2) \\$

几何意义：向量与标量相乘可以改变向量的长度，而保持向量的方向不变。

1.3.5 向量与向量相乘

向量与向量相乘是一个广义的概念，根据具体的数学定义和应用场景，可以有多种不同的解释。

1.3.5.1 点积（内积）

点积是两个向量之间的一种乘法运算，其结果是一个标量（单一数值）。公式为：

$\mathbf{a} \cdot \mathbf{b} = |\mathbf{a}| |\mathbf{b}| \cos\theta \\$

其中：

$|\mathbf{a}|$ 和 $|\mathbf{b}|$ 分别是向量的模（长度）。
$\theta$ 是两个向量之间的夹角。

在二维或三维空间中，点积也可以用分量表示：

$\mathbf{a} \cdot \mathbf{b} = a_1 b_1 + a_2 b_2 + a_3 b_3 \\$

几何意义：点积可以用来计算两个向量之间的夹角，或者判断两个向量是否正交（如果点积为0，则两向量正交）。

应用：

计算投影长度。
判断两个向量的方向关系。

1.3.5.2 叉积（外积、向量积）

叉积是两个向量之间的一种乘法运算，其结果是一个向量。公式为：

$\mathbf{a} \times \mathbf{b} = |\mathbf{a}| |\mathbf{b}| \sin\theta \, \mathbf{n} \\$

其中：

$|\mathbf{a}|$ 和 $|\mathbf{b}|$ 分别是向量的模。
$\theta$ 是两个向量之间的夹角。
$\mathbf{n}$ 是垂直于 $\mathbf{a}$ 和 $\mathbf{b}$ 所在平面的单位向量（方向由右手定则确定）。

在三维空间中，叉积可以用行列式表示：

$\mathbf{a} \times \mathbf{b} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix} \\$

几何意义：叉积的结果是一个垂直于原两个向量的向量，其模长等于两个向量所构成的平行四边形的面积。

应用：

计算平面法向量。
物理中的力矩、角动量等。

1.3.5.3 逐元素乘积（Hadamard 积）

逐元素乘积是指将两个向量对应位置的元素相乘，得到一个新的向量。例如：

$\mathbf{a} = [a_1, a_2, a_3], \quad \mathbf{b} = [b_1, b_2, b_3] \\$

则：

$\mathbf{a} \odot \mathbf{b} = [a_1 b_1, a_2 b_2, a_3 b_3] \\$

应用：

图像处理中的像素操作。
深度学习中的张量计算。

1.3.5.4 外积（张量积）

外积是一种更广义的乘法运算，其结果是一个矩阵（张量）。对于两个向量 $\mathbf{a}$ 和 $\mathbf{b}$ ，外积定义为：

$\mathbf{a} \otimes \mathbf{b} = \mathbf{a} \mathbf{b}^\top \\$

即：

$\mathbf{a} = [a_1, a_2, a_3]^\top, \quad \mathbf{b} = [b_1, b_2, b_3]^\top \\$

则：

$\mathbf{a} \otimes \mathbf{b} = \begin{bmatrix} a_1 b_1 & a_1 b_2 & a_1 b_3 \\ a_2 b_1 & a_2 b_2 & a_2 b_3 \\ a_3 b_1 & a_3 b_2 & a_3 b_3 \end{bmatrix} \\$

应用：

线性代数中的张量分析。
量子力学中的态矢量运算。

1.3.5.5. 总结

点积：结果是标量，用于计算角度或投影。
叉积：结果是向量，用于计算垂直向量或面积。
逐元素乘积：结果是向量，用于逐元素操作。
外积：结果是矩阵，用于张量运算。

1.4. 在计算机图形学中定义颜色

在计算机图形学中，颜色通常用一个三元组（RGB）或四元组（RGBA）来表示。其中，RGB 代表红绿蓝三种颜色分量，RGBA 则是在 RGB 的基础上增加了透明度（Alpha）分量。这些分量通常用 0 到 255 之间的整数来表示，也可以用 0.0 到 1.0 之间的浮点数来表示。例如，红色可以用 (255, 0, 0) 或 (1.0, 0.0, 0.0) 来表示，蓝色可以用 (0, 0, 255) 或 (0.0, 0.0, 1.0) 来表示。在图形学中，颜色通常用浮点数来表示，因为浮点数可以表示更精细的颜色值，而且可以方便地进行颜色混合和插值操作。

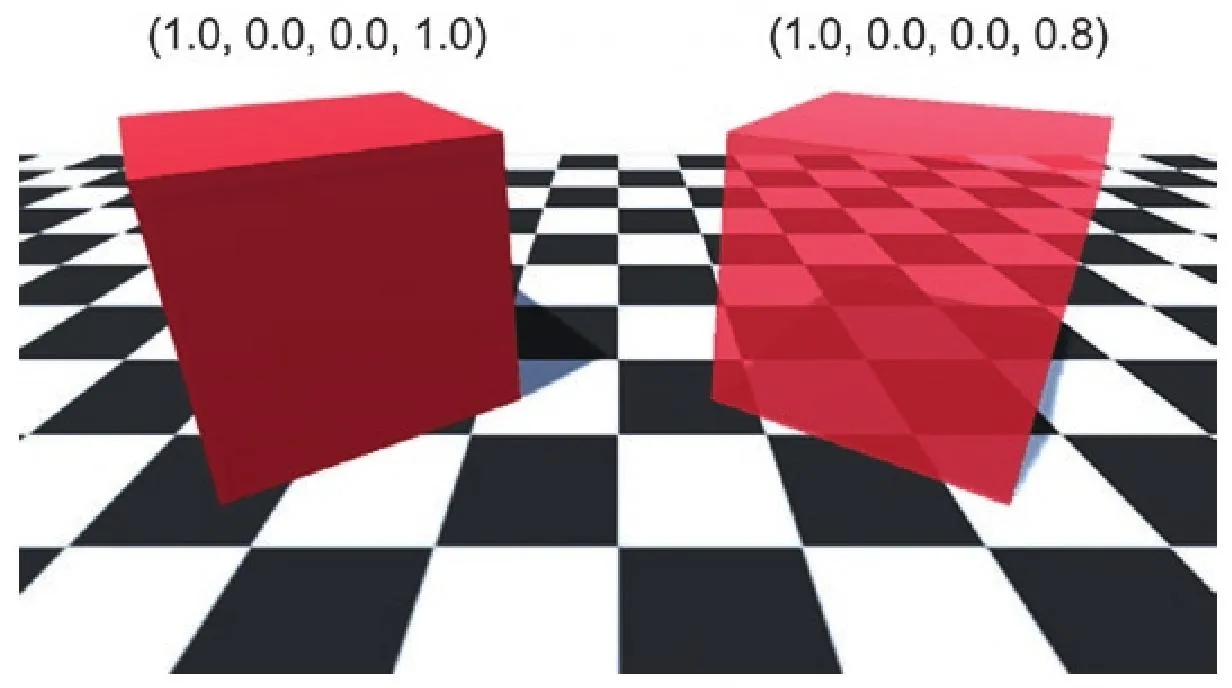左边立方体的alpha值为1，右边立方体的alpha值为0.8，可以看到右边的立方体颜色更透明。

1.5. 渲染管线

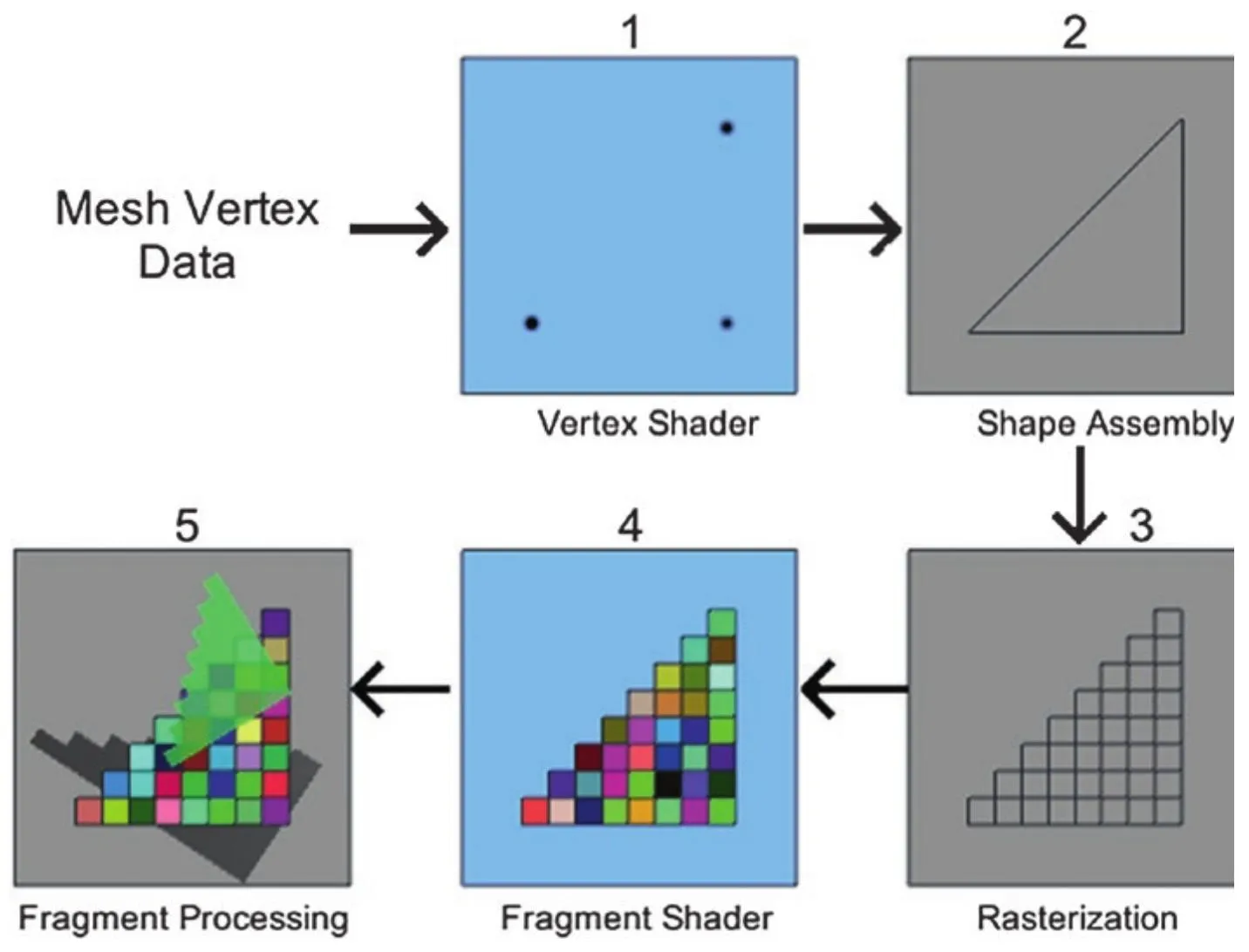
渲染管线是一个复杂的过程，它将顶点数据转换为像素数据，然后将像素数据输出到屏幕上。渲染管线通常由以下几个步骤组成：

顶点着色器：将顶点数据转换为屏幕坐标。
图元装配：将顶点数据转换为图元。
光栅化：将图元转换为像素。
片段着色器（片元着色器）：将像素数据转换为颜色。
片元处理：对像素数据进行一些处理，分为片元测试和混合操作。
- 片元测试：决定哪些片元可以被渲染到屏幕上，哪些片元不能被渲染到屏幕上。片元为网格生成的，没有任何关于场景其余部分的信息，这意味着GPU通常创建的片元比屏幕要填充的像素多
- 混合操作：将像素颜色与屏幕上的颜色进行混合。

1.5.1. 片元与像素的区别

在图形学中，片元（Fragments）和像素（Pixels）是两个相关但不完全相同的概念。

像素（Pixel）：指的是屏幕上显示的最小单位。每个像素都有自己的颜色值，由红、绿、蓝（RGB）三原色组成。在最终的图像输出中，我们看到的就是这些像素组成的画面。
片元（Fragment）：是指在光栅化阶段生成的对象，它包含了成为屏幕上一个像素所需的所有数据，如颜色、深度值等。片元是在着色器程序处理过程中产生的，可能会经过各种测试（如深度测试、模板测试等），只有通过了这些测试的片元才会真正影响到对应的像素的颜色值。因此，并不是所有的片元都会最终转换为像素，有些片元可能在到达屏幕之前就被丢弃了。

简而言之，片元可以被视为潜在的像素，它们在通过一系列测试并被确认对图像的最终外观有贡献之后，就会变成实际的像素。在这个过程中，片元着色器（Fragment Shader）负责计算每个片元的颜色和其他属性。这个过程对于实现各种高级的图形效果非常重要，比如光照、阴影、反射等。

1.6. 着色器

我们将重点关注顶点着色器和片段着色器，因为它们是渲染管线的核心部分。顶点着色器接收顶点数据作为输入，并输出顶点位置、颜色、纹理坐标等。片段着色器接收像素数据作为输入，并输出像素颜色。这两个着色器都是可编程的，这意味着我们可以使用自己编写的代码来控制它们的行为。本书使用OpenGL作为图形库，因此使用 GLSL（OpenGL Shading Language）的语言来编写，它是一种基于 C 语言的编程语言，具有类似 C 语言的语法。GLSL 语言提供了许多内置函数和变量，可以用来进行数学运算、向量操作、矩阵操作等。着色器代码通常被编译成二进制代码，然后被发送到 GPU 上执行。GPU 上的着色器代码被分成多个小块，每个小块都可以在不同的线程上并行执行。这种并行执行的能力使得 GPU 可以同时处理大量的像素，从而实现高性能的渲染。

posted @ 2025-03-27 23:02 龙湾开发阅读(49) 评论(0) 收藏举报

刷新页面返回顶部

OpenGLshader开发实战学习笔记：第一章 初识游戏图形