考研C语言数据结构-二叉树(二叉树的链式存储实现 + 常见题型解法)

二叉树的结构如图：

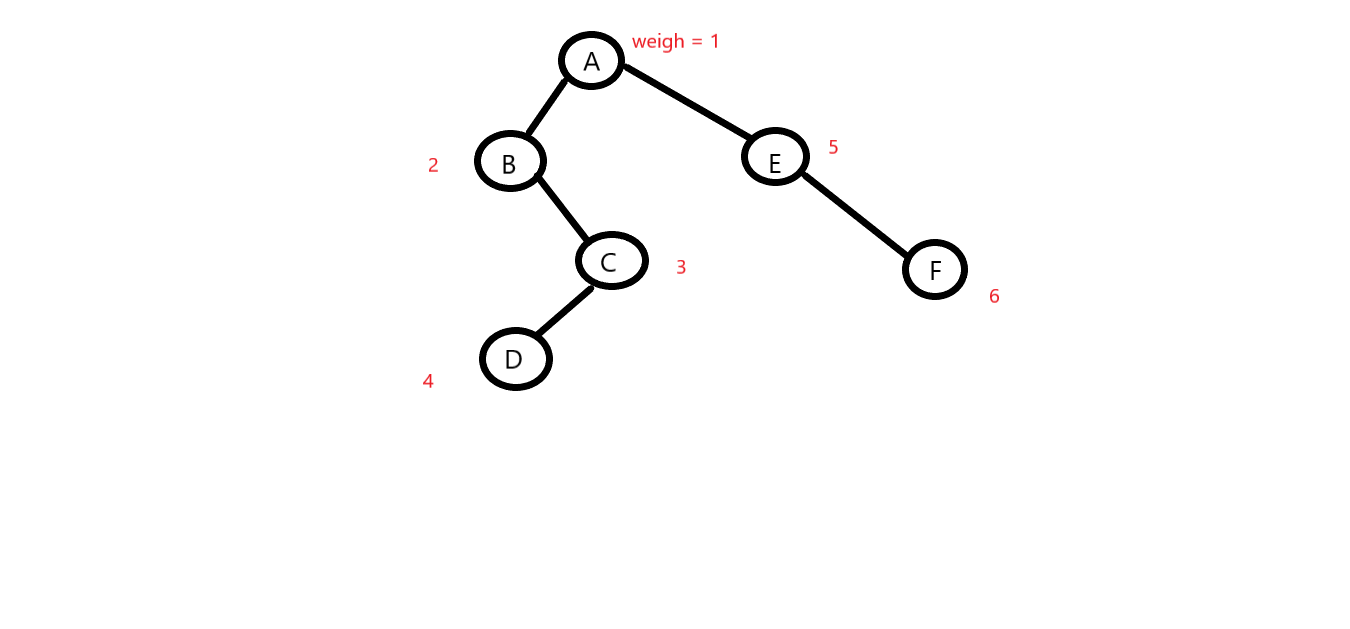
二叉树的存储实现：

#include <stdio.h>
#include <stdlib.h>

// 定义结点数据类型
typedef struct TNode {

	char data;
	struct TNode *lChild, *rChild;
	int weight; // 权值
}TNode, *BiTree;

// 初始化二叉树
void initBiTree(BiTree &T) {

	TNode *A = (TNode *)malloc(sizeof(TNode));
	A->data = 'A';
	A->weight = 1;
	A->lChild = NULL;
	A->rChild = NULL;

	TNode *B = (TNode *)malloc(sizeof(TNode));
	B->data = 'B';
	B->weight = 2;
	B->lChild = NULL;
	B->rChild = NULL;

	A->lChild = B;

	TNode *C = (TNode *)malloc(sizeof(TNode));
	C->data = 'C';
	C->weight = 3;
	C->lChild = NULL;
	C->rChild = NULL;

	B->rChild = C;

	TNode *D = (TNode *)malloc(sizeof(TNode));
	D->data = 'D';
	D->weight = 4;
	D->lChild = NULL;
	D->rChild = NULL;

	C->lChild = D;

	TNode *E = (TNode *)malloc(sizeof(TNode));
	E->data = 'E';
	E->weight = 5;
	E->lChild = NULL;
	E->rChild = NULL;

	A->rChild = E;

	TNode *F = (TNode *)malloc(sizeof(TNode));
	F->data = 'F';
	F->weight = 6;
	F->lChild = NULL;
	F->rChild = NULL;

	E->rChild = F;

	T = A;
}

// 先序遍历
void preOrder(BiTree T) {

	if(T != NULL) {
	
		printf("先序遍历结点值:%c\n", T->data);
		preOrder(T->lChild);
		preOrder(T->rChild);
	}
}

// 中序遍历
void inOrder(BiTree T) {

	if(T != NULL) {
	
		inOrder(T->lChild);
		printf("中序遍历结点值:%c\n", T->data);
		inOrder(T->rChild);
	}
}

// 后序遍历
void postOrder(BiTree T) {

	if(T != NULL) {
	
		postOrder(T->lChild);
		postOrder(T->rChild);
		printf("后序遍历结点值:%c\n", T->data);
	}
}

// 定义结点数据类型
typedef struct LNode {

	TNode* data;
	struct LNode *next;
}LNode;

// 定义链队数据类型
typedef struct {

	LNode *front, *rear;
}LiQueue;

void initLiQueue(LiQueue &Q) {

	Q.front = Q.rear = (LNode *)malloc(sizeof(LNode));
	Q.front->next = NULL;
}

// 判断队列空
bool isEmpty(LiQueue Q) {

	if(Q.front == Q.rear)
		return true;

	return false;
}

// 入队操作
void enQueue(LiQueue &Q, TNode* T) {

	LNode *p = (LNode *)malloc(sizeof(LNode));

	p->data = T;

	p->next = NULL;

	Q.rear->next = p;

	Q.rear = p;
}

// 出队操作
bool deQueue(LiQueue &Q, TNode* &T) {

	if(isEmpty(Q))
		return false;

	LNode *p = Q.front->next;

	T = p->data;

	Q.front->next = p->next;

	// 如果出队元素是队列的最后一个元素,需要修改尾指针
	if(p == Q.rear)
		Q.rear = Q.front;

	free(p);

	return true;
}

// 层序遍历
void levelOrder(BiTree T) {

	LiQueue Q;
	initLiQueue(Q);

	// 根节点入队
	enQueue(Q, T);

	TNode * p = NULL;

	while(!isEmpty(Q)) {
	
		deQueue(Q, p);
		printf("层序遍历结点值:%c\n", p->data);

		if(p->lChild != NULL)
			enQueue(Q, p->lChild);

		if(p->rChild != NULL)
			enQueue(Q, p->rChild);
	}
}

// 二叉树叶子节点的统计
void calculateLeafNodes(BiTree T, int &leafNodes) { // leafNodes 初始值0

	if(T != NULL) {
	
		calculateLeafNodes(T->lChild, leafNodes);
		calculateLeafNodes(T->rChild, leafNodes);

		if(T->lChild == NULL && T->rChild == NULL)
			leafNodes++;
	}
}

// 求二叉树深度操作
int calculateDepth(BiTree T)
{
    if (T == NULL)
        return 0; //如果是空树，深度为0，递归结束
    else
    {
		int leftHeight = calculateDepth(T->lChild); //递归计算左子树的深度记为leftHeight
		int rightHeight = calculateDepth(T->rChild); //递归计算右子树的深度记为rightHeight
        if (leftHeight > rightHeight)
            return (leftHeight + 1); //二叉树的深度为leftHeight 与rightHeight的较大者加1
        else
            return (rightHeight + 1);
    }
}

// 利用先序遍历计算树的带权路径长度(WPL)
void calculateWPL(BiTree T, int deep, int &WPL) {// deep, WPL初始为0

	if(T->lChild == NULL && T->rChild == NULL)
		WPL += deep * T->weight;

	if(T->lChild != NULL)
		calculateWPL(T->lChild, deep + 1, WPL);

	if(T->rChild != NULL)
		calculateWPL(T->rChild, deep + 1, WPL);
}

// 求二叉树根结点至某一结点的路径序列
// 定义结点数据类型
typedef struct LSNode {

	TNode * data; // 数据域
	struct LSNode *next; // 指针域
}LSNode, *LiStack;

// 初始化链栈(带头结点)
void initLiStack(LiStack &S) {

	S = (LSNode *)malloc(sizeof(LSNode));

	S->next = NULL;
}

// 判断栈空
bool isEmpty(LiStack S) {

	if(S->next == NULL)
		return true;

	return false;
}

// 入栈(头插法LIFO)
void push(LiStack &S, TNode * T) {

	LSNode *p = (LSNode *)malloc(sizeof(LSNode));

	p->data = T;

	p->next = S->next;

	S->next = p;
}

// 出栈
bool pop(LiStack &S, TNode * &T) {

	if(isEmpty(S))
		return false;

	LSNode *p = S->next;

	T = p->data;

	S->next = p->next;

	free(p);

	return true;
}

// 求二叉树根结点至某一结点的路径序列
void calculateTrack(BiTree T, char ch, LiStack &S, bool &flag) {// flag 初始为false

	if(T->data == ch) {
	
		push(S, T);
		flag = true;
		return;
	}

	if(T->lChild != NULL && !flag) {
	
		calculateTrack(T->lChild, ch, S, flag);
		if(flag)
			push(S, T);
	}

	if(T->rChild != NULL && !flag) {
	
		calculateTrack(T->rChild, ch, S, flag);
		if(flag)
			push(S, T);
	}
}

int main(void) {

	BiTree T;

	initBiTree(T);

	preOrder(T);
	printf("\n");

	inOrder(T);
	printf("\n");

	postOrder(T);
	printf("\n");

	levelOrder(T);
	printf("\n");

	int leafNodes = 0;
	calculateLeafNodes(T, leafNodes);
	printf("二叉树叶子结点数:%d\n", leafNodes);
	printf("\n");

	int height = calculateDepth(T);
	printf("二叉树的深度:%d\n", height);
	printf("\n");

	int WPL = 0;
	calculateWPL(T, 0, WPL);
	printf("二叉树的带权路径长度WPL:%d\n", WPL);
	printf("\n");

	LiStack S;
	initLiStack(S);
	bool flag = false;
	calculateTrack(T, 'D', S, flag);
	TNode * t = NULL;
	while(!isEmpty(S)) {
	
		pop(S, t);
		printf("从根结点A至'D'的路径为:%c\n", t->data);
	}

	system("pause");
	return 0;
}