BZOJ4987 Tree 树形dp

BZOJ 4987 Tree

题目描述

在树中找 \(k\)个点，\(A1,A2,...,Ak\)

使得\(∑dis(AiAi+1),(1<=i<=K-1)\) 最小。

解题思路

首先肯定是想到把任意两个点之间的距离贡献拆开，变成\(dis(u)+dis(v)-2*dis(lca(u,v))\)

然后我们继续观察这个贡献（然而我是后面才观察到），除了开头和结尾，中间每个点会贡献\(2*dep(u)\) ，我们考虑设状态\(dp[u][i][0/1/2]\) 表示子树u内选了i个点，开头和结尾的数目，最小代价。

一开始我想的直接贪心的合并，

\[0+0->0\\ 0+1->1\\ 1+0->1\\ 1+1->2 \]

上面的01表示状态的转移。很好理解，就是两个选了1个端点的链直接贪心的lca处合并。但是交上去，它\(wa\)了。

得到一个奇妙的菊花数据，发现还有一种情况没有考虑。我们可以先不合并两个1，中间填上若干0，然后再合并。这样就是完备的了。

所以这道题启示我们，不要上来就贪心，要仔细思考所有可能有的状态。

上面的转移可以加上两个：

\[2+0->2 \\ 0+2->2 \]

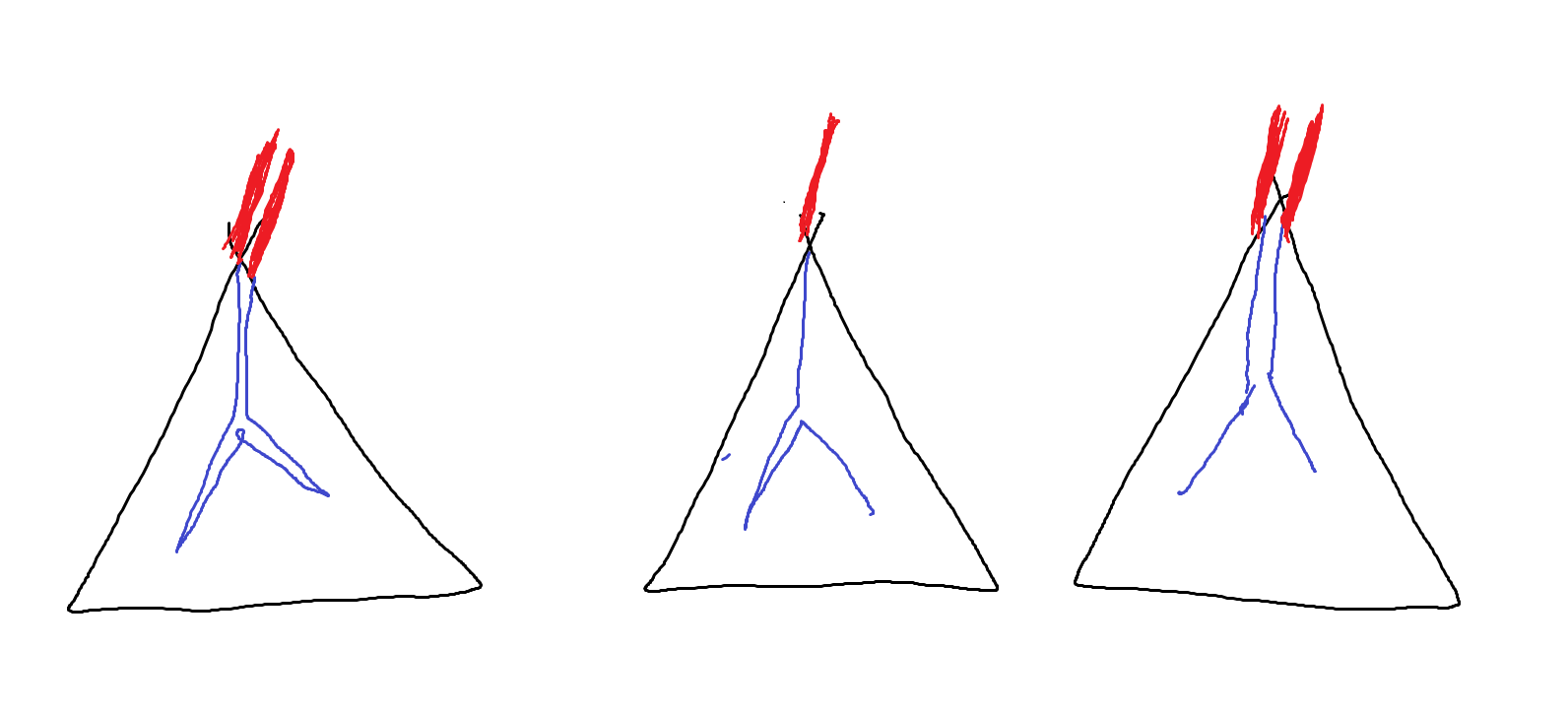
附上分的情况的图，转载自GXZlegend

#include<bits/stdc++.h>
using namespace std;
const int N = 3e3 + 11;
int n, K;
int head[N], to[N<<1], wei[N<<1], nex[N<<1], size;
int dis[N], dp[N][N][3], tmp[N][3], ans[N];
int sz[N];
void add(int x, int y, int z){
    to[++size] = y;
    nex[size] = head[x];
    head[x] = size;
    wei[size] = z;
}
void dfs(int u, int fa){
    for(int i = head[u];i;i = nex[i]){
        int v = to[i];
        if(v == fa)continue;
        dis[v] = dis[u] + wei[i];
        dfs(v, u);
    }
}
void dfs1(int u, int fa){
    dp[u][0][0] = 0;
    dp[u][1][0] = 2 * dis[u];
    dp[u][1][1] = dis[u];
    sz[u] = 1;
    for(int i = head[u];i;i = nex[i]){
        int v = to[i];
        if(v == fa)continue;
        dfs1(v, u);
        for(int j = 0;j <= sz[u] && j <= K; j++){
            for(int k = 0;k <= sz[v] && k + j <= K; k++){
                tmp[j+k][0] = min(tmp[j+k][0], dp[v][k][0] + dp[u][j][0] + (j > 0 && k > 0) * (-2 * dis[u]));
                tmp[j+k][1] = min(tmp[j+k][1], dp[v][k][0] + dp[u][j][1] - (k > 0) * 2 * dis[u]);
                tmp[j+k][1] = min(tmp[j+k][1], dp[v][k][1] + dp[u][j][0] - (j > 0) * 2 * dis[u]);
                tmp[j+k][2] = min(tmp[j+k][2], dp[v][k][1] + dp[u][j][1]);
                tmp[j+k][2] = min(tmp[j+k][2], dp[v][k][2] + dp[u][j][0] - 2 * dis[u] * (j > 0));
                tmp[j+k][2] = min(tmp[j+k][2], dp[v][k][0] + dp[u][j][2] - 2 * dis[u] * (k > 0));
                if(j > 0)ans[j+k] = min(ans[j+k], dp[v][k][2] + dp[u][j][0] - 4 * dis[u]);
                if(k > 0)ans[j+k] = min(ans[j+k], dp[v][k][0] + dp[u][j][2] - 4 * dis[u]);
                ans[j+k] = min(ans[j+k], dp[v][k][1] + dp[u][j][1] - 2 * dis[u]);
            }
        }
        sz[u] += sz[v];
        for(int j = 0;j <= K; j++){
            for(int k = 0;k <= 2; k++){
                dp[u][j][k] = min(dp[u][j][k], tmp[j][k]);
                tmp[j][k] = dp[0][0][0];
            }
        }
        /*printf("u=%d\n", u);
        for(int i = 0;i <= K; i++){
            printf("i=%d %d %d %d\n", i, dp[u][i][0], dp[u][i][1], dp[u][i][2]);
        }
        puts("");*/
    }

}
int main(){
    freopen("4987.in", "r", stdin);
    freopen("4987.out", "w", stdout);
    cin>>n>>K;
    int u, v, w;
    for(int i = 1;i < n; i++){
        scanf("%d%d%d", &u, &v, &w);
        add(u, v, w); add(v, u, w);
    }
    memset(dp, 127 / 2, sizeof dp);
    memset(tmp, 127 / 2, sizeof tmp);
    memset(ans, 127 / 2, sizeof ans);
    dfs(1, 0);
    dfs1(1, 0);
    cout<<ans[K]<<endl;
    return 0;
}