QBXT 2018春季DP&图论班 2018.4.29 --- 最短路&差分约束

*钟皓曦老师授课*

常见最短路算法：

Floyd → O(n^3)

//floyd

int dist[maxn][maxn];

memset(dist,0x3f,sizeof(dist));
for (int a=1;a<=m;a++)
{
    int s,e,d;
    cin >> s >> e >> d;
    dist[s][e] = min(dist[s][e],d);
    //可能会有重边 
}
for (int a=1;a<=n;a++)
    dist[a][a] = 0;
    
for (int a=1;a<=n;a++)
    for (int b=1;b<=n;b++)
        for (int c=1;c<=n;c++)
        dist[b][c] = min(dist[b][c],dist[b][a]+dist[a][c]);
    
    

Bellman-Ford → O(nm)

    
//Bellman-Ford

for (int a=1;a<=m;a++)
    cin >> s[a] >> e[a] >> d[a];
memset(dist,0x3f,sizeof(dist));
dist[1]=0;

for (int a=1;a<=n;a++)
    for (int b=1;b<=m;b++)
        dist[e[b]] = min(dist[e[b]],dist[s[b]]+d[b]);

Dijkstra → O(n^2+m)

cin >> n >> m;
for (int a=1;a<=m;a++) {
    int s,e;
    cin >> s >> e >> d;
    add_edge(s,e,d);
}
memset(dist,0x3f,sizeof(dist));
dist[1]=0;
bool in_left[maxn];
for (int a=1;a<=n;a++)
{
    int nowp=0;
    for (int b=1;b<=n;b++)
        if (in_left[b] == false && 
            (nowp==0 || dist[b]<dist[nowp]))
            nowp = b;
    in_left[nowp] = true;
    for (edge *e=v[nowp];e;e=e->next)
        dist[e->e] = min(dist[e->e],dist[nowp]+e->d);
}

Dijkstra-Heap → O((n+m)log(n+m))

//dijkstra + heap
#include<queue>

using namespace std;

struct rec
{
    int p,d;
    rec() {p=d=0;}
    rec(int a,int b) {
        p=a;d=b;
    }
}rqy;

gaojing a,b,c;
c=a+b;

int aplusb(int a,int b);
bool operator<(const rec &a,const rec &b) {
    return a.d>b.d;
}
priority_queue<rec> heap;
cin >> n >> m;
for (int a=1;a<=m;a++) {
    int s,e;
    cin >> s >> e >> d;
    add_edge(s,e,d);
}
memset(dist,0x3f,sizeof(dist));
dist[1]=0;
for (int a=1;a<=n;a++)
    heap.push(rec(a,dist[a]));
bool in_left[maxn];
for (int a=1;a<=n;a++)
{
    while (in_left[heap.top().p])
        heap.pop();
    rec now = heap.top();
    heap.pop();
    int nowp=now.p;
    in_left[nowp] = true;
    for (edge *e=v[nowp];e;e=e->next)
    {
        int newd = dist[nowp] + e->d;
        if (newd < dist[e->e]) {
            dist[e->e] = newd;
            heap.push(rec(e->e,newd));
        }
    }
}

SPFA → O(km) 随机图 （k一般为2） 可以判负环→若一个点进队列次数超过n次，则有负环。

　　　  O(nm) 精心构造的数据

#include<queue>

using namespace std;

queue<int> que;
memset(dist,0x3f,sizeof(dist));
dist[1]=0;
que.push(1);
while (que.size())) {
    int now=que.front();
    que.pop();
    in_queue[now] = false;
    for (edge *e=v[now];e;e=e->next)
    {
        int newd = dist[now] + e->d;
        if (newd < dist[e->e]) {
            dist[e->e] = newd;
            if (!in_queue[e->e]) {
                in_queue[e->e] = true;
                que.push(e->e);
            }
        }
    }
}

→判断选用哪种算法：

if(n<=100) Floyd;

else if(无负权) Dijkstra-Heap;

　　else SPFA;

→

①单源最短路可以求解多源最短路问题。

②一点到另一点的最短路，最多经过n-1条边。

　　→证明：若路径包含的边数>=n，说明有环，我们可以去掉环之后直接走。因此最短路不存在环，也就最多只有n-1条边。

③求最短路一定无负环，求最长路一定无正环。但可以有正负权值的边。

次短路（次短简单路，即无重复点）：

①枚举每一条边，删除后跑最短路，最后取min O(n*(n+m)log(n+m))。

②令dis[u][0]表示从起点到u的最短路，dis[u][1]表示从起点到u的次短路。

 

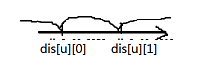
设W=dis[v][0]+e[i].w

当W∈左集合时 即新更新的最短路<之前最短路<之前次短路 ∴dis[v][1]=dis[v][0],dis[v][0]=W

当W∈中间集合时 即之前最短路<新更新的最短路<之前次短路 ∴dis[v][1]=W dis[v][0]不变

当W∈右集合时 即之前最短路<之前次短路<新更新的最短路 ∴dis[v][1]和dis[v][0]都不变

任何一个点的次短路可能有多段次短路组合而成，因此最终ans还要用次短路更新一遍。

//次短简单路
for (edge *e=v[now];e;e=e->next)
for (int op=0;op<=1;op++)
{
    int v=dist[now][op]+e->d;
    int i=e->e;
    if (v<=dist[i][0]) {
        dist[i][1] = dist[i][0];
        dist[i][0] = v;
    }
    else {
        if (v<=dist[i][1]) dist[i][1]=v;
    }
}

PS.对于次短非简单路，用A*或ZEN（蒙特卡洛）算法，不考，而且我也不会。。。。

K短路：（目前不会。。。，但方法和上面类似）

差分约束：

给定n个变量，m个形如vi-vj</<=/>/>=/= k 的约束条件，令v1=0，求vn最小/最大是多少。

<=>n个点，m条边，从v1号点出发，问vn的最长路/最短路是多少。

例：v1-v3>=3   ①v1>=v3+3 根据最长路三角不等式，v3向v1连一条边权为3的边。建完图后跑最长路

　　　　　　　②v3<=v1+(-3) 根据最短路三角不等式，v1向v3连一条边权为-3的边。建完图后跑最短路、

最大值<=>最短路  若存在负环，则最大值为无穷大

最小值<=>最长路  若存在正环，则最小值为无穷小

例：{v1-v2>=3 ; v2-v3>=3 ; v1-v3>=2 }

①最大值

{v2<=v1+(-3) ; v3<=v2+(-3) ; v3<=v1+(-2)}

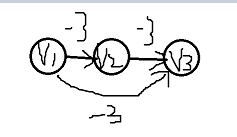
∵从v1到v3的最短路为-6

∴ v3 max=-6

②最小值

{v1>=v2+3 ; v2>=v3+3 ; v1>=v3+2}

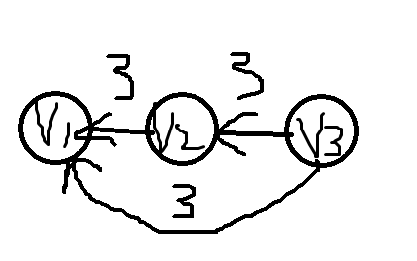
∵从v1到v3的最长路不存在

∴v3 min=  -∞

常见连边方式：

vi-vj>=k -> vi>=vj+k or vj<=vi+(-k)

vi-vj>k -> vi-vj>=k+1

vi-vj=k -> vi-vj>=k&&vi-vj<=k -> vi>=vj+k&&vi<=vj+k 连两条边，形成一个零环，使两者最短/长路相等

vi-vj<=k

vi-vj<k ->vi-vj<=k-1