《python数据分析(第2版)-阿曼多.凡丹戈》读书笔记第6章-数据可视化
第6章数据可视化
数据分析初始阶段,我们通常都要进行可视化处理。借助图示技术,就算枯燥的数值表,也可以展示出它婀娜的一面。数据可视化旨在直观展示信息的分析结果和构思,令某些抽象数据具象化,这些抽象数据包括数据测量单位的性质或数量。数据可视化与科学可视化和统计图示技术关系极为紧密。本章用到的程序库Matplotlib是建立在NumPy之上的一个Python绘图库,它提供了一个面向对象的API和一个过程式类MATLAB API,它们可以并行使用。Matplotlib使用的图库可以从其官网页面下载。下面我们给出本章涉及的主题。
- Matplotlib的子库
- Matplotlib简单绘图
- 对数图
- 散点图
- 图例和注解
- 三维图
- Pandas绘图
- 时滞图
- 自相关图
- Plot.ly
6.1Matplotlib的子库
如果我们对本书代码包中的ch-01.ipynb后面部分代码稍作修改,就可以列出Matplotlib的各个子库,结果如下。
1 import pkgutil as pu 2 import numpy as np 3 import matplotlib as mpl 4 import scipy as sp 5 import pandas as pd 6 import pydoc 7 8 print("Matplotlib version", mpl.__version__) 9 10 def clean(astr): 11 s = astr 12 # remove multiple spaces 13 s = ' '.join(s.split()) 14 s = s.replace('=','') 15 16 return s 17 18 def print_desc(prefix, pkg_path): 19 for pkg in pu.iter_modules(path=pkg_path): 20 name = prefix + "." + pkg[1] 21 22 if pkg[2] == True: 23 try: 24 docstr = pydoc.plain(pydoc.render_doc(name)) 25 docstr = clean(docstr) 26 start = docstr.find("DESCRIPTION") 27 docstr = docstr[start: start + 140] 28 print(name, docstr) 29 except: 30 continue 31 32 print("\n") 33 print_desc("matplotlib", mpl.__path__)
这些子程序包的名称基本上不解自明,唯一需要说明的是,这里的后缀backends指的是最终结果的输出方式,即可以通过某种格式的文件输出结果,也可以通过图形用户界面输出到屏幕上。
Matplotlib version 3.2.1 matplotlib.axes matplotlib.backends matplotlib.cbook DESCRIPTION A collection of utility functions and classes. Originally, many (but not all) were from the Python Cookbook -- hence the name cb matplotlib.compat matplotlib.projections matplotlib.sphinxext matplotlib.style matplotlib.testing matplotlib.tri
6.2Matplotlib绘图入门
第1章介绍了Matplotlib和IPython的安装方法,如果需要,我们可以回头去看。Matplotlib采用了类似MATLAB的过程式API,这种接口的易用性通常明显优于面向对象的API,因此,我们首先会演示过程式API的使用方法。为了使用Matplotlib来绘制基本图形,我们需要调用matplotlib.pyplot子库中的plot()函数。如果数据点具有x和y坐标,我们就可以使用这个函数来绘制由这种数据点组成的单个或多个数据表的二维图像了。
此外,我们还可以通过格式化参数来指定虚线样式。Plot()函数的格式选项和参数非常多,可以通过下面的命令查看(需要提前导入matplotlib.pyplot库)。
1 import matplotlib.pyplot as plt 2 #查看帮助 3 print(help(plt.plot))
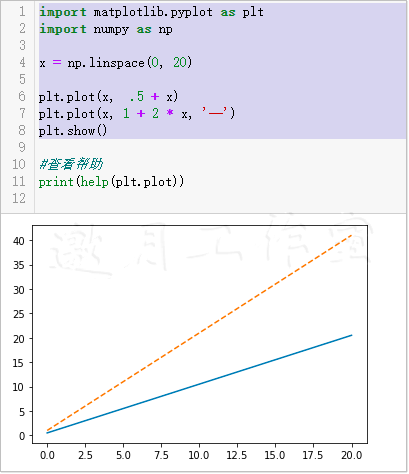
本例要使用两种样式来绘制线条,即实线(默认样式)和虚线。
下列演示代码引自本书代码包中的ch-06.ipynb文件。
1 import matplotlib.pyplot as plt 2 import numpy as np 3 4 x = np.linspace(0, 20) 5 6 plt.plot(x, .5 + x) 7 plt.plot(x, 1 + 2 * x, '--') 8 plt.show()
为了画出上述线条,我们要执行以下步骤。
(1)首先,通过NumPy中的linspace()函数指定横坐标,同时规定起点和终点分别为0和20。
x = np.linspace(0, 20)
(2)其次通过下列代码画线。
1 plt.plot(x, .5 + x) 2 plt.plot(x, 1 + 2 * x, ‘—‘)
此时,既可以用savefig()函数把图形保存到一个文件中,也可以通过show()函数将图形显示到屏幕上。将图形显示到屏幕上所需的代码如下。
1 plt.show()
最终结果如图6-1所示。
6.3对数图
所谓对数图,实际上就是使用对数坐标绘制的图形。对于对数刻度来说,其间隔表示的是变量的值在数量级上的变化,这与线性刻度有很大的不同。对数图又分为两种不同的类型,其中一种称为双对数图,它的特点是两个坐标轴都采用对数刻度,对应的matplotlib函数是matplotlib.pyplot.loglog()。另一种,半对数图的一个坐标轴采用线性标度,另一个坐标轴使用对数刻度,它对应的matplotlib API是semilogx()函数和semilogy()函数。在双对数图上,幂律表现为直线;在半对数图上,直线则代表的是指数律。
摩尔定律就是这样一种增长方式。当然,这不是一条物理定律,而是对经验观测值的一种刻画。摩尔定律是由戈登·摩尔(Gordon Moore)提出来的,大意为集成电路上晶体管的数目,约每两年增加一倍。网上有一个数据表,记录了不同年份微处理器上晶体管的数量。
我们已经为这个数据表制作了一个CSV文件,名为transcount.csv,其中仅含有年份和晶体管数目。此外,我们还需要计算晶体管数量的年度平均值。至于计算平均值和加载该文件的方法,可以由Pandas代劳,如果需要,可以回顾第4章介绍的方法。求出数据表中晶体管数目的年度平均值后,就可以一条直线来拟合晶体管数量随年份的变化了。NumPy中的polyfit()函数可以用多项式来拟合数据。
下列代码引自本书代码包中的ch-06.ipynb文件。
1 import matplotlib.pyplot as plt 2 import numpy as np 3 import pandas as pd 4 5 df = pd.read_csv('transcount.csv') 6 df = df.groupby('year').aggregate(np.mean) 7 years = df.index.values 8 counts = df['trans_count'].values 9 poly = np.polyfit(years, np.log(counts), deg=1) 10 print("Poly", poly) 11 plt.semilogy(years, counts, 'o') 12 plt.semilogy(years, np.exp(np.polyval(poly, years))) 13 plt.show()
下面介绍以上代码。
(1)拟合数据,代码如下。
1 poly = np.polyfit(years, np.log(counts), deg=1) 2 print("Poly", poly)
(2)经过拟合,得到一个Polynomial对象,该对象的详情可参考网上的介绍。这个对象的字符串表示,实际上就是多项式系数的按次数降序排列,因此,最高次数项的系数在最前面。就我们的数据而言,得到的多项式系数如下。
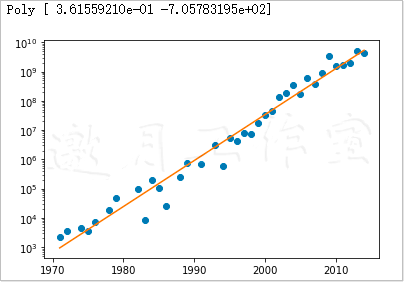
Poly [ 3.61559210e-01 -7.05783195e+02]
(3)NumPy的polyval()函数可以用来对上面得到的多项式进行评估。下面我们为数据绘制图像并通过semilogy()函数进行拟合。
1 plt.semilogy(years, counts, 'o') 2 plt.semilogy(years, np.exp(np.polyval(poly, years)))
这里,实线表示的是趋势线,实心圆表示的是数据点。最终结果如图6-2所示。
6.4散点图
散点图可以形象展示直角坐标系中两个变量之间的关系。在散点图中,每个数据点的位置实际上就是两个变量的值。变量之间的任何关系都可以拿散点图来示意。上升趋势模式通常意味着正相关。泡式图是对散点图的一种扩展。在泡式图中,每个数据点都被一个气泡所包围,它由此得名;而第3个变量的值正好可以用来确定气泡的相对大小。
在WiKi网站上,也有一个记录图形处理单元(GPU)晶体管数量的数据表。
GPU是为了高效显示图像而专门设计的。得益于现代显卡的工作机制,GPU能以高度并行的方式来处理数据。可以说,GPU是计算技术新时代的弄潮儿。对于本书代码包中的gpu_transcount.csv文件,我们没有为它提供太多的数据点。处理缺失数据是泡式图经常要面对的一个问题,对于缺失数据,需要为其定义一个默认的气泡大小。下面,我们再次载入年度数据并计算其平均值,然后通过外部连接操作,按照年份对存放CPU和GPU晶体管数量的DataFrame进行合并。这当中,NaN值将被设为0。需要注意的是,就本例而言是可以将NaN值设为0的,但是其他情况下却未必如此。所有这些功能都已经在第4章中讲过了,如有需要,读者可以重新温习一下。为了绘制散点图和泡式图,我们可以借助matplotlib API提供的scatter()函数。要想查阅这个函数的相关说明文档,我们可以使用以下命令。
1 $ ipython3 2 import matplotlib as mpl 3 help(mpl.scatter)
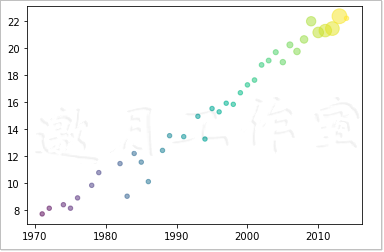
本例中,需要设置参数s,这个参数与气泡的大小有关。另外,还有一个参数c,用来指定气泡的颜色。令人遗憾的是,本书非彩色印刷,无法展示气泡的颜色,读者只有亲自运行示例代码,才能看到不同的颜色。这里参数alpha的作用是,决定图中气泡的透明度。这个值为0~1,其中0代表完全透明,1代表完全不透明。创建泡式图的代码如下。
plt.scatter(years, cnt_log, c= 200 * years, s=20 + 200 * gpu_counts/gpu_counts.max(), alpha=0.5)
下列代码引自本书代码包中的ch-06.ipynb文件。
1 import matplotlib.pyplot as plt 2 import numpy as np 3 import pandas as pd 4 5 df = pd.read_csv('transcount.csv') 6 df = df.groupby('year').aggregate(np.mean) 7 8 gpu = pd.read_csv('gpu_transcount.csv') 9 gpu = gpu.groupby('year').aggregate(np.mean) 10 11 df = pd.merge(df, gpu, how='outer', left_index=True, right_index=True) 12 df = df.replace(np.nan, 0) 13 years = df.index.values 14 counts = df['trans_count'].values 15 gpu_counts = df['gpu_trans_count'].values 16 cnt_log = np.log(counts) 17 plt.scatter(years, cnt_log, c= 200 * years, s=20 + 200 * gpu_counts/gpu_counts.max(), alpha=0.5) 18 plt.show()
最终结果如图6-3所示。
6.5图例和注解
要想做出让人一眼就懂的“神图”,图例和注解肯定是少不了的。一般情况下,数据图都带有下列辅助信息。
- 用来描述图中各数据序列的图例。为此,可以使用matplotlib提供的legend()函数,来给每个数据序列提供相应的标签。
- 对图中要点的注解。为此,可以借助matplotlib提供的annotate()函数。Matplotlib生成的注解包括标签和箭头两个组成部分。这个函数提供了多个参数,用以描述标签和箭头样式以及其位置。如果想详细了解这些参数,调用help(annotate)函数即可。
- 横轴和纵轴的标签。这些标签可以通过xlabel()和ylabel()函数绘制出来。对于这两个函数,我们需要提供一个字符串来作为标签的文本,另外还要提供一些可选参数,如标签的字体大小等。
- 一个说明性质的标题,通常由matplotlib的title()函数来提供。一般来说,这个函数只要提供一个描述标题的字符串即可。
- 网格,对于轻松定位数据点非常有帮助。Matplotlib提供的grid()函数可以用来决定是否启用网格。
下面对上例中的泡式图程序代码稍作修改,加入本章第2个例子中的直线。同时,还会为数据序列添加一个标签,相关代码如下。
1 plt.plot(years, np.polyval(poly, years), label='Fit') 2 plt.scatter(years, cnt_log, c= 200 * years, s=20 + 200 * gpu_counts/gpu_counts.max(), alpha=0.5, label="Scatter Plot")
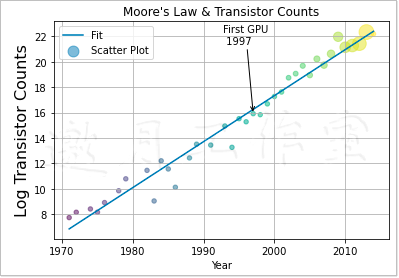
现在给数据集中的第一个GPU添加注释。为此,需要指定相关的数据点,为注解定义标签,指定箭头样式(见参数arrowprops),同时还要确保把注解置于相应数据点之上。
1 gpu_start = gpu.index.values.min() 2 y_ann = np.log(df.at[gpu_start, 'trans_count']) 3 ann_str = "First GPU\n %d" % gpu_start 4 plt.annotate(ann_str, xy=(gpu_start, y_ann), arrowprops=dict(arrowstyle="->"), xytext=(-30, +70), textcoords='offset points')
要想阅读完整的代码,请参阅本书代码包中的ch-06.ipynb文件。
1 import matplotlib.pyplot as plt 2 import numpy as np 3 import pandas as pd 4 5 df = pd.read_csv('transcount.csv') 6 df = df.groupby('year').aggregate(np.mean) 7 gpu = pd.read_csv('gpu_transcount.csv') 8 gpu = gpu.groupby('year').aggregate(np.mean) 9 10 df = pd.merge(df, gpu, how='outer', left_index=True, right_index=True) 11 df = df.replace(np.nan, 0) 12 years = df.index.values 13 counts = df['trans_count'].values 14 gpu_counts = df['gpu_trans_count'].values 15 16 poly = np.polyfit(years, np.log(counts), deg=1) 17 plt.plot(years, np.polyval(poly, years), label='Fit') 18 19 gpu_start = gpu.index.values.min() 20 y_ann = np.log(df.at[gpu_start, 'trans_count']) 21 ann_str = "First GPU\n %d" % gpu_start 22 plt.annotate(ann_str, xy=(gpu_start, y_ann), arrowprops=dict(arrowstyle="->"), xytext=(-30, +70), textcoords='offset points') 23 24 cnt_log = np.log(counts) 25 plt.scatter(years, cnt_log, c= 200 * years, s=20 + 200 * gpu_counts/gpu_counts.max(), alpha=0.5, label="Scatter Plot") 26 plt.legend(loc='upper left') 27 plt.grid() 28 plt.xlabel("Year") 29 plt.ylabel("Log Transistor Counts", fontsize=16) 30 plt.title("Moore's Law & Transistor Counts") 31 plt.show()
最终结果如图6-4所示。
6.6三维图
对数据可视化来说,二维图像只是家常便饭,要是想来点大餐,那就非三维图形莫属了。原书作者负责开发了一个软件包,用它就可以绘制等高线图和三维图。如果我们戴上一副特制眼镜的话,该软件绘图时,图像宛如从我们面前跃出一般。
Axes3D是由matplotlib API提供的一个类,可以用来绘制三维图。通过讲解这个类的工作机制,就能够明白面向对象的matplotlib API的原理了。Matplotlib的Figure类是存放各种图像元素的顶级容器。
(1)首先,创建一个Figure对象,代码如下。
fig = plt.figure()
(3)利用Figure对象创建一个Axes3D对象。
ax = Axes3D(fig)
(3)这里,令x轴和y轴分别表示年份和CPU晶体管数量。同时,我们还需要利用存放年份和CPU晶体管数量的数组来创建坐标矩阵(coordinate matrices)。创建坐标矩阵时,可以借助NumPy中的meshgrid()函数。
X, Y = np.meshgrid(X, Y)
(4)通过Axes3D类的plot_surface()方法为数据绘制图像。
ax.plot_surface(X, Y, Z)
(5)根据面向对象API函数的命名约定,应该以set_开头,以程序对应的函数名结尾,具体如下。
1 ax.set_xlabel('Year') 2 ax.set_ylabel('Log CPU transistor counts') 3 ax.set_zlabel('Log GPU transistor counts') 4 ax.set_title("Moore's Law & Transistor Counts")
下列代码摘自本书代码包中的ch-06.ipynb文件。
1 from mpl_toolkits.mplot3d.axes3d import Axes3D 2 import matplotlib.pyplot as plt 3 import numpy as np 4 import pandas as pd 5 6 df = pd.read_csv('transcount.csv') 7 df = df.groupby('year').aggregate(np.mean) 8 gpu = pd.read_csv('gpu_transcount.csv') 9 gpu = gpu.groupby('year').aggregate(np.mean) 10 11 df = pd.merge(df, gpu, how='outer', left_index=True, right_index=True) 12 df = df.replace(np.nan, 0) 13 14 fig = plt.figure() 15 ax = Axes3D(fig) 16 X = df.index.values 17 18 #Y = np.log(df['trans_count'].values) 19 Y = np.where(df['trans_count'].values>0, np.log(df['trans_count'].values), 0) 20 X, Y = np.meshgrid(X, Y) 21 #Z = np.log(df['gpu_trans_count'].values) 22 Z = np.where(df['gpu_trans_count'].values>0, np.log(df['gpu_trans_count'].values), 0) 23 24 ax.plot_surface(X, Y, Z) 25 ax.set_xlabel('Year') 26 ax.set_ylabel('Log CPU transistor counts') 27 ax.set_zlabel('Log GPU transistor counts') 28 ax.set_title("Moore's Law & Transistor Counts") 29 plt.show()
最终结果如图6-5所示。
#第22行报错:RuntimeWarning: divide by zero encountered in log, # Argument Z must be 2-dimensional."
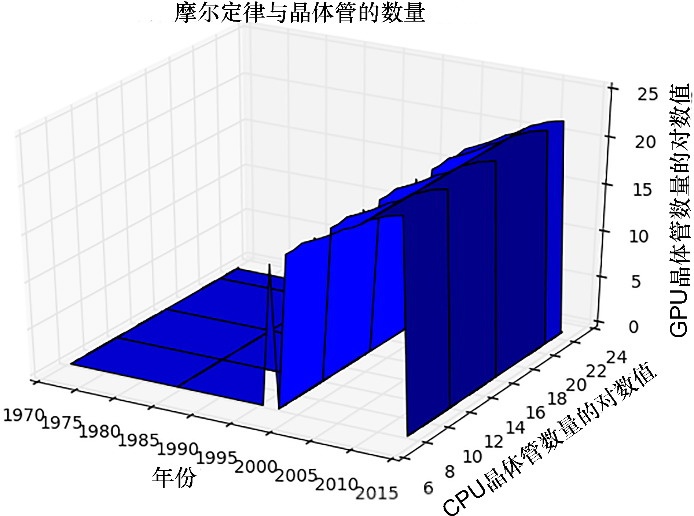
6.7Pandas绘图
Pandas的Series类和DataFrame类中的plot()方法都封装了相关的matplotlib函数。如果不带任何参数,使用plot()方法绘制本章一直用的那个数据集,将会得到图6-6所示的图像。
与下图合并。
为了创建半对数图,我们需要增设logy参数。
df.plot(logy=True)
我们的数据生成的图像如图6-7所示。
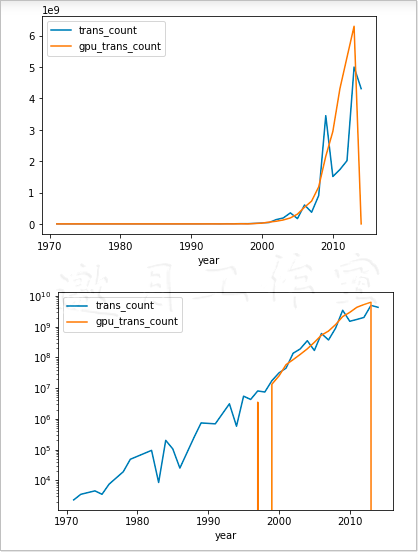
为了创建散点图,我们需要把参数kind设为scatter,同时,还要指定两个列。此外,如果我们将参数loglog设为True,就会生成一个双对数(log-log)图。注意,下列代码要求Pandas的版本最低为0.13.0。
Df[df[‘gpu_trans_count’] > 0].plot(kind=’scatter’, x=’trans_count’,
Y=’gpu_trans_count’, loglog=True)
最终结果如图6-8所示。
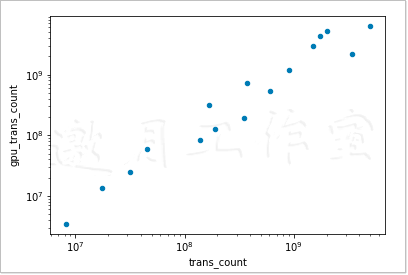
下面的代码摘自本书代码包中的ch-06.ipynb文件。
1 import matplotlib.pyplot as plt 2 import numpy as np 3 import pandas as pd 4 5 df = pd.read_csv('transcount.csv') 6 df = df.groupby('year').aggregate(np.mean) 7 8 gpu = pd.read_csv('gpu_transcount.csv') 9 gpu = gpu.groupby('year').aggregate(np.mean) 10 11 df = pd.merge(df, gpu, how='outer', left_index=True, 12 right_index=True) 13 df = df.replace(np.nan, 0) 14 df.plot() 15 df.plot(logy=True) 16 df[df['gpu_trans_count'] > 0].plot(kind='scatter', 17 x='trans_count', y='gpu_trans_count', loglog=True) 18 plt.show()
6.8时滞图
时滞图实际上就是一幅散点图,只不过把时间序列的图像及相同序列在时间轴上后延的图像放在一起展示而已。举例来说,我们可以利用这种图来考察今年的CPU晶体管数量与上一年度CPU晶体管数量之间的相关性。我们可以利用Pandas子库pandas.tools.plotting中的lag_plot()函数来绘制时滞图。下面是绘制CPU晶体管数量时滞图的代码,这里时滞默认为1,具体如下。
lag_plot(np.log(df[‘trans_count’]))
最终结果如图6-9所示。
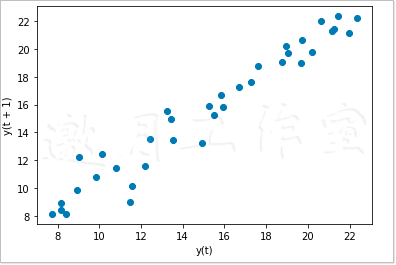
下面是用来演示时滞图的示例代码,摘自本书代码包中的ch-06.ipynb文件。
1 import matplotlib.pyplot as plt 2 import numpy as np 3 import pandas as pd 4 from pandas.plotting import lag_plot 5 6 df = pd.read_csv('transcount.csv') 7 df = df.groupby('year').aggregate(np.mean) 8 9 gpu = pd.read_csv('gpu_transcount.csv') 10 gpu = gpu.groupby('year').aggregate(np.mean) 11 12 df = pd.merge(df, gpu, how='outer', left_index=True, right_index=True) 13 df = df.replace(np.nan, 0) 14 lag_plot(np.log(df['trans_count'])) 15 plt.show()
6.9自相关图
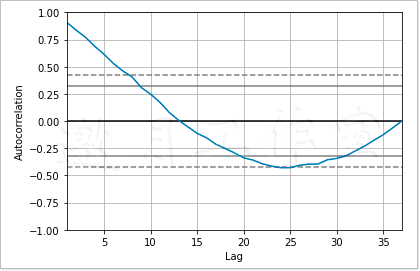
自相关图描述的是时间序列数据在不同时间延迟情况下的自相关性。所谓自相关,用非专业人员的话说,就是时间序列在时刻n的值与在时刻n+l的值的相互关系,其中l就是这里的时间延迟。通常,这些图用于检查时间序列是否具有随机性。就随机时间序列来说,对于所有时间延迟其自相关值接近于零;而对于非随机时间序列,对于某些或所有时间延迟来说自相关值都会具有显著的非零值。我们将在第7章中进一步详细说明自相关性。
利用Pandas子库pandas.tools. plotting中的autocorrelation_plot()函数,我们就可以画出自相关图了。下列演示代码摘自本书代码包中的ch-06.ipynb文件。
1 import matplotlib.pyplot as plt 2 import numpy as np 3 import pandas as pd 4 from pandas.plotting import autocorrelation_plot 5 6 df = pd.read_csv('transcount.csv') 7 df = df.groupby('year').aggregate(np.mean) 8 9 gpu = pd.read_csv('gpu_transcount.csv') 10 gpu = gpu.groupby('year').aggregate(np.mean) 11 12 df = pd.merge(df, gpu, how='outer', left_index=True, right_index=True) 13 df = df.replace(np.nan, 0) 14 autocorrelation_plot(np.log(df['trans_count'])) 15 plt.show()
为CPU晶体管数量绘制自相关图的代码如下。
autocorrelation_plot(np.log(df[‘trans_count’]))
从图6-10中可以看出,较之于时间上越远(即时间延迟越大)的数值,当前的数值与时间上越接近(即时间延迟越小)的数值的相关性越大;当时间延迟极大时,相关性衰减为0。
6.10Plot.ly
Plot.ly实际上是一个网站,目前处于beta测试阶段。它不仅提供了许多数据可视化的在线工具,同时还提供了可在用户机器上使用的对应Python库。我们可以通过Web接口或以本地方式导入并分析数据,而且还可以将分析结果公布到Plot.ly网站上面。团队内的各个成员可以通过这个网站轻松达到共享数据图像的目的,从而实现成员之间的协作,这也正是该网站的独到之处。本节我们将举例说明如何通过Python API来绘制箱形图。
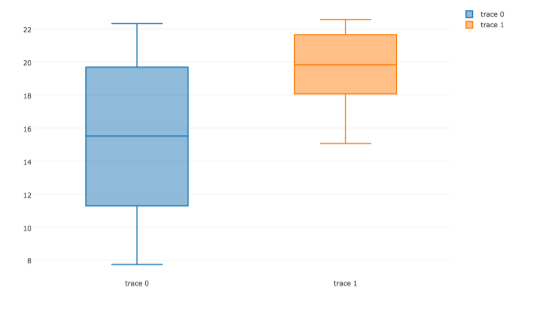
箱形图是一种通过四分位数来形象展示数据集的特殊方法。如果把一个有序数据集分为4等份,那么第1个四分位数就是最小值区间的最大值。第2个四分位数是位于数据集中间位置的那个数值,又称“中位数”。第3个四分位数是位于中位数和最大值中间位置上的那个数值。箱形图的顶和底分别是第1个四分位数和第3个四分位数,而贯穿箱子的那条线则是中位数。箱子顶底上的那两根“须”,通常就是数据集的最大值和最小值。本节结束时,我们会提供一幅带有注释的箱形图,届时就会一目了然了。安装Plot.ly API的命令如下。
pip3 install plotly
pip install chart-studio
安装API后,我们注册获得一个API密钥,提供有效密钥后,可以通过下列代码登录。
# Change the user and api_key to your own username and api_key py.sign_in('username', 'api_key')
通过Plot.ly API创建箱形图的代码如下。
1 data = Data([Box(y=counts), Box(y=gpu_counts)]) 2 plot_url = py.plot(data, filename='moore-law-scatter')
下列代码摘自本书代码包中的ch-06.ipynb文件(plotly.plotly改为chart_studio.plotly)。
1 import chart_studio.plotly as py 2 from plotly.graph_objs import * 3 import numpy as np 4 import pandas as pd 5 6 df = pd.read_csv('transcount.csv') 7 df = df.groupby('year').aggregate(np.mean) 8 9 gpu = pd.read_csv('gpu_transcount.csv') 10 gpu = gpu.groupby('year').aggregate(np.mean) 11 df = pd.merge(df, gpu, how='outer', left_index=True, right_index=True) 12 df = df.replace(np.nan, 0) 13 14 # Change the user and api_key to your own username and api_key 15 py.sign_in('username', 'api_key') 16 17 counts = np.log(df['trans_count'].values) 18 gpu_counts = np.log(df['gpu_trans_count'].values) 19 20 data = Data([Box(y=counts), Box(y=gpu_counts)]) 21 plot_url = py.plot(data, filename='moore-law-scatter') 22 print(plot_url)
最终结果如图6-11所示。
6.11小结
本章论述了基于Python的数据可视化,其中用到了Matplotlib、Pandas和Plot.ly,同时还讲解了箱形图、散点图、泡式图、对数图、自相关图、时滞图、三维图、图例和注解等。
对数图是使用对数坐标绘制的图形;半对数图是一个坐标轴使用线性标度,另一个坐标轴使用对数标度画出的图形。散点图描绘的是两个变量之间的对应关系,而泡式图则是一种特殊的散点图。在泡式图中,第3个变量的值表示的是包围数据点的气泡的大小。自相关图描绘的是时间序列数据对于不同时间延迟的自相关性。
同时,我们还介绍了plot.ly,它是一个用于数据可视化的在线云服务,而且使用该服务创建了一个箱型图。箱型图是根据数据的四分位数来形象展示数据的一种可视化方法。
第 7 章将介绍一种特殊类型的数据:时间序列。时间序列是一些按时间先后顺序排列形成的数据点,当然,这些数据点都提前按照时间戳做了标记。许多物理世界的测量数据都是以时间序列的形式存在的并且一般都被视为信号,如声音信号、光信号或者电信号等。后续章节我们不仅会教大家如何过滤这些信号,而且会介绍如何对时间序列进行建模。
第6章完。
随书源码官方下载:
https://www.ptpress.com.cn/shopping/buy?bookId=bae24ecb-a1a1-41c7-be7c-d913b163c111
需要登录后免费下载。
 阿曼多·凡丹戈(Armando Fandango)的《python数据分析(第2版)》,2018年6月出版,本系列为读书笔记。主要是为了系统整理,加深记忆。第6章“数据可视化”介绍如何利用Matplotlib和Pandas的绘图函数来实现数据的可视化。
阿曼多·凡丹戈(Armando Fandango)的《python数据分析(第2版)》,2018年6月出版,本系列为读书笔记。主要是为了系统整理,加深记忆。第6章“数据可视化”介绍如何利用Matplotlib和Pandas的绘图函数来实现数据的可视化。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号