《数据分析实战-托马兹.卓巴斯》读书笔记第10章--离散选择模型理论
第10章解释了选择模型理论以及一些流行的模型:多项式Logit模型、嵌套Logit模型以及混合Logit模型。
本章中,会学习以下技巧:
·准备数据集以估算离散选择模型
·估算知名的多项Logit模型
·测试来自无关选项的独立性冲突
·用巢式Logit模型处理IIA冲突
·用混合Logit模型处理复杂的替代模式
10.1导论
DCM(Discrete choice models,离散选择模型)的目标是预测出一个人会做怎样的选择。这些模型与逻辑回归有共同之处,但在误差项的分布假设方面又有不同。
DCM以随机效用理论作为理论基础,并假设一个理性的人,总是做出使效用最大化的选择。
例如,假设你要做一个二选一的决定(这两个选项是没有共同点的);我们考虑选择骑自行车还是开车去上班的情形。骑自行车几乎无成本(当然,这里假设你已经有一辆自行车了,也忽略了骑自行车消耗的能量),而开车的成本是3块钱。骑自行车上班要花45min,而开车只要8min。假设价格系数和时间系数分别是-2和-0.13,可以计算出,骑自行车的效用是-5.85,开车的效用是-7.04。所以,在效用最大化的假设下,你会选择骑自行车,而不是开车。这个简化的计算不考虑性格偏好因素。
我们生成用于本章技巧的数据集,是西雅图与洛杉矶之间4个航班16个等级中做出的10000个选择;各选项的详情如下: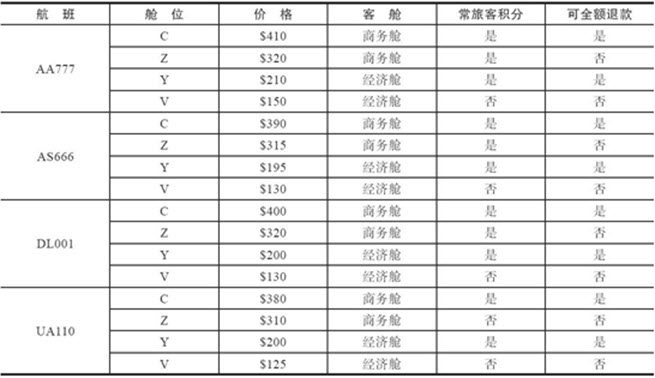
下一章会介绍如何转换这个数据集,用于估算多种DCM。
我们使用Python Biogeme估算DCM,这是由Michel Bierlaire博士在Bierlaire,M.(2003);BIOGEME:A free package for the estimation of discrete choice models中发表的。虽然不是纯Python(估算的引擎是用C++写的),但这是估算DCM最好的开源软件。Python Biogeme还在活跃更新中,可从http://biogeme.epfl.ch下载;径直访问Download部分,选择你的操作系统对应的版本。由于软件包是免费的,因此你需要在Yahoo的Biogeme用户群中注册:https://groups.yahoo.com/neo/groups/biogeme/info。
下载软件包之后,按照http://biogeme.epfl.ch/install.html上的指南安装。装好后就可以通过下面的命令调用了:
>>pythonbiogeme <model_file> <dataset>
注意:这段话来自原书作者
/*
我们使用软件包时遇到了问题。这个软件包要求Python 3.2之上的版本。尽管本书使用的是Python 3.5(安装在~/anaconda文件夹中),
但是Python Biogeme会到/usr/local/Frameworks/Python.framework/Versions/3.5路径下寻找Python,这个路径在我们的机器上根本不存在。
我们只好手动创建这个路径,然后重新安装软件。 我们也在Windows上试了,可以正常运行。不过,有些朋友可能会在安装和运行时遇到问题,这也是要大家注意一下的。 如果你遇到了任何问题,你可以在Biogeme用户群中询问;一般很快就有回复了。如果你实在没法子了,也可以给原作者发邮件,mail@tomdrabas.com,能帮的原作者一定帮。 */
以下来自邀月的安装步骤:
/* pip install biogeme Looking in indexes: https://pypi.tuna.tsinghua.edu.cn/simple Collecting biogeme Using cached https://pypi.tuna.tsinghua.edu.cn/packages/40/aa/cbad1883d2914451e0714981ec2332e443dabfe5b5d874199dfbc1070b98/biogeme-3.2.5-cp37-cp37m-win_amd64.whl (816 kB) Requirement already satisfied: scipy in d:\tools\python37\lib\site-packages (from biogeme) (1.4.0) Requirement already satisfied: numpy in d:\tools\python37\lib\site-packages (from biogeme) (1.18.2) Requirement already satisfied: cython in d:\tools\python37\lib\site-packages (from biogeme) (0.29.14) Requirement already satisfied: pandas in d:\tools\python37\lib\site-packages (from biogeme) (0.25.3) Requirement already satisfied: unidecode in d:\tools\python37\lib\site-packages (from biogeme) (1.1.1) Requirement already satisfied: python-dateutil>=2.6.1 in d:\tools\python37\lib\site-packages (from pandas->biogeme) (2.8.1) Requirement already satisfied: pytz>=2017.2 in d:\tools\python37\lib\site-packages (from pandas->biogeme) (2019.3) Requirement already satisfied: six>=1.5 in d:\tools\python37\lib\site-packages (from python-dateutil>=2.6.1->pandas->biogeme) (1.12.0) Installing collected packages: biogeme Successfully installed biogeme-3.2.5 FINISHED */
10.2准备数据集以估算离散选择模型
为这些技巧准备的数据包括了10000条选择情形。第一列是选择的ID,第二列是用户可选的选项列表;不是所有情形下都要从所有选项中选择。
准备:需要安装好pandas、NumPy和正则表达式模块。
步骤:Python Biogeme要求数据以制表符分隔,每一行包括所有选项的属性、选出的选项以及做出选择时每个选项是否可选。值的类型只能是数字。下面的代码可在dcm_dataPrep.py文件中看到:
1 import pandas as pd 2 import numpy as np 3 import re 4 5 # read datasets 6 choices_filename = '../../Data/Chapter10/choices.csv' 7 alternatives_filename = '../../Data/Chapter10/options.json' 8 9 choices = pd.read_csv(choices_filename) 10 alternatives = pd.read_json(alternatives_filename).transpose() 11 12 # retrieve all considered alternatives 取回所有考虑的选项 13 considered = [alt.split(';') 14 for alt in list(choices['available'])] 15 16 # create flag of all available alternatives 标出所有可能的选项 17 available = [] 18 alternatives_list = list(alternatives.index) 19 alternatives_list = [ 20 re.sub(r'\.', r'_', alt) for alt in alternatives_list] 21 no_of_alternatives = len(alternatives_list) 22 23 for cons in considered: 24 f = [0] * len(alternatives_list) 25 26 cons = [re.sub(r'\.', r'_', alt) for alt in cons] 27 28 for i, alt in enumerate(alternatives_list): 29 if alt in cons: 30 f[i] = 1 31 32 available.append(list(f)) 33 34 # append to the choices DataFrame 追加到选项DataFrame中 35 alternatives_av = [alt + '_AV' for alt in alternatives_list] 36 available = pd.DataFrame(available, columns=alternatives_av) 37 choices = choices.join(available) 38 39 # drop the available column as we don't need it anymore 40 #丢掉不需要的列 41 del choices['available'] 42 43 # encode the choice variable 编码选择变量 44 choice = list(choices['choice']) 45 choice = [re.sub(r'\.', r'_', alt) for alt in choice] 46 choice = [alternatives_list.index(c) + 1 for c in choice] 47 48 choices['choice'] = pd.Series(choice) 49 50 # and add the alternatives' attributes 加上选项属性 51 # first, normalize price to be between 0 and 1 首先,将价格归一为0到1之间的数 52 max_price = np.max(alternatives['price']) 53 alternatives['price'] = alternatives['price'] / max_price 54 55 # next, create a vector with all attributes 然后,创建所有选项的向量 56 attributes = [] 57 attributes_list = list(alternatives.values) 58 59 for attribute in attributes_list: 60 attributes += list(attribute) 61 62 # fill in to match the number of rows 填充以匹配行数 63 attributes = [attributes] * len(choices) 64 65 # and their names 名字 66 attributes_names = [] 67 68 for alternative in alternatives_list: 69 for attribute in alternatives.columns: 70 attributes_names.append(alternative + '_' + attribute) 71 72 # convert to a DataFrame 转化为DataFrame 73 attributes = pd.DataFrame(attributes, 74 columns=attributes_names) 75 76 # and join with the main dataset 和主数据集连接 77 choices = choices.join(attributes) 78 79 # save as a TSV with .dat extension 输出为.dat文件 80 with open('../../Data/Chapter10/choices.dat', 'w') as f: 81 f.write(choices.to_csv(sep='\t', index=False))
原理:按照惯例,我们先导入会用到的模块。
数据集位于本书Git仓库的Data/Chapter10/文件夹中。它已拆成两个文件:observations.csv是那10000个选择样本,options.json是带上属性的所有选项。
observations.csv文件格式如下:
/* choice available AA777.4.V AA777.1.C;AA777.2.Z;AA777.4.V;AS666.1.C;AS666.3.Y;AS666.4.V;DL001.2.Z;DL001.3.Y;DL001.4.V;UA110.1.C;UA110.3.Y;UA110.4.V UA110.3.Y AA777.1.C;AA777.2.Z;AA777.3.Y;AA777.4.V;AS666.1.C;AS666.2.Z;AS666.4.V;DL001.2.Z;UA110.2.Z;UA110.3.Y;UA110.4.V DL001.1.C AA777.1.C;AA777.2.Z;AA777.3.Y;AA777.4.V;AS666.3.Y;AS666.4.V;DL001.1.C;DL001.3.Y;UA110.3.Y;UA110.4.V */
第一列是做出的选择:比如选择了AA777航班的V等级。用户是从12个选项中选择的:用;分隔的12个选项的列表。
options.json文件格式如下:
/* { "AA777.1.C": { "compartment": 1, "frequentFlyer": 1, "price": 410, "refund": 1 }, "AA777.2.Z": { "compartment": 1, "frequentFlyer": 1, "price": 320, "refund": 0 }, */
compartment值为1表示是商务舱,frequentFlyer和refund都为1,意味着可以累计常旅积分,并可以免费退票。
使用pandas读取CSV与JSON格式的文件,参考本书1.2节。
读入数据集后,我们先关注考虑的选项列表。从choices DataFrame对象提取出可选的列,并将行拆成独立的选项。我们将用这个创建一个带有所有可选选项的DataFrame对象。
要做到这一点,需要所有可选选项的列表。从DataFrame对象alternatives提取所有索引。不过这些值里包含了点号,比如AA777.1.C。如果直接使用Python Biogeme会有问题,所以用re包的.sub(...)方法将点号替换成下划线。
注意,正则表达式r'.'匹配的是除换行符之外的所有字符,所以要用r'\.'。
.sub(...)方法以正则表达式为第一个参数,以替代字符串为第二个参数,以要处理的字符串为第三个参数。
最后,遍历所有记录,标出可选的选项。首先,创建和选项一样多的0。然后,为了兼容alternatives_list,也替换了cons里的点号。最后,遍历所有选项,将其中可用的标为1。最后得到了这样的列表: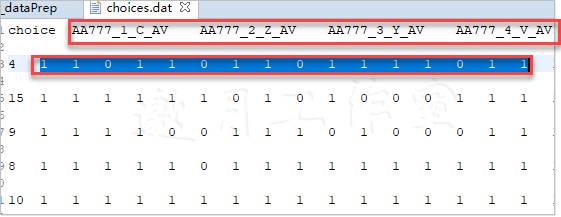
创建相应的列名,以便在Python Biogeme中使用;要达到这一目标,在每个选项的名字后加上_AV后缀。
最后,创建一个DataFrame对象available,其中包含可用选项的向量,与DataFrame对象choices连接,并删除后面用不到的available列:
与上图合并
可以看到,选择了AA777航班的V等级,和期望的一样,这是决策者的考虑。
然后,需要给choice列中的选项编码。首先,取出DataFrame中的所有记录,并用下划线替换点号。接着,遍历所有元素,找到alternatives_list中元素的.index(...)。这样做之后,我们和数据集的其余部分保持一致。最后,用投射到pandas的Series对象中已编码的choice列表替换choice列。
最后一项是往数据集中加所有选项的所有属性。前面提过,数据集中的每一行需要包括所有选项的所有信息。
就本例而言,这是相同信息的列表,自顶而下。不过,这种处理方式一般在处理更普通的选项时会有用得多,比如,用火车还是用汽车,这个时候价格和距离可能都不同。如果数据集有不同的目的地,每一行会有不同的属性。
首先,将价格归一化到0和1之间。直接从数据集中取出最大价格,然后所有价格都除以这个值。也可以用Python Biogeme做到这一点,但是推荐直接处理,仅仅用Python Biogeme估算模型。
然后,提取DataFrame对象alternatives的.values属性,以获取所有属性的值。attributes_list本质上就是一个NumPy数组列表(pandas的默认数据结构很多都由NumPy承袭而来):
/* [array([1., 1., 1., 1.]), array([1. , 1. , 0.7804878, 0. ]), array([0. , 1. , 0.51219512, 1. ]), array([0. , 0. , 0.36585366, 0. ]), array([1. , 1. , 0.95121951, 1. ]), array([1. , 1. , 0.76829268, 0. ]), array([0. , 1. , 0.47560976, 1. ]), array([0. , 0. , 0.31707317, 0. ]), array([1. , 1. , 0.97560976, 1. ]), array([1. , 1. , 0.7804878, 0. ]), array([0. , 1. , 0.48780488, 1. ]), array([0. , 0. , 0.31707317, 0. ]), array([1. , 1. , 0.92682927, 1. ]), array([1. , 0. , 0.75609756, 0. ]), array([0. , 1. , 0.48780488, 1. ]), array([0. , 0. , 0.30487805, 0. ])] */
因为我们需要一个带有所有属性的大向量,所以遍历attributes_list,并给每个数组扩展attributes列表。对于这10000行,都要复制一遍,所以将attributes列表乘以choices的长度,即行数。
再之后,为所有属性创建列名。创建好attributes列表并放置好列名后,创建一个DataFrame对象,并与初始数据集连接。
最后一步,将数据集导出成一个.dat文件,以制表符分隔(以与Biogeme的传统保持一致)。
更多::如果你的数据集是CSV格式,你可以使用Biogeme的biopreparedata工具创建数据集。另外,biocheckdata可用于检查数据集是否符合Biogeme的标准。
10.3
估算知名的多项Logit模型
MNL(Multinomial Logit,多项Logit)模型是由Daniel McFadden于1973年在其研讨会论文中提出的,http://eml.berkeley.edu/reprints/mcfadden/zarembka.pdf。
这个模型基于十分严格的假设:IID(Independent and Identically Distributed,独立同分布)的误差项和IIA(Independence from Irrelevant Alternatives,独立于无关选项)。
IID假设所有选项效用函数的误差项是独立(不相干)的,并服从同样的分布。(就MNL而言,I型极值分布,一般称为Gumbel分布,这是以发现并分析这个分布的E.J.Gumbel命名的。)
另一方面,IIA假设选项间可能性的比率是一个常量,即,从考虑范围中移除一个选项,不会改变其余选项的比率。考虑这样一个场景:你要从自行车、火车、汽车中挑一个作为上班的交通工具。假设每个选项的可能性是相同的,也就是每项被选中的概率都是1/3。在IIA假设下,如果汽车坏了,那么另两项的比率保持恒定,即被选中的可能性是一半一半。下一技巧会解释为什么这是个严格假设。
MNL中的概率计算式如下:
截图(公式)![]()
U(i)是每个选项的效用,定义为:
截图(公式)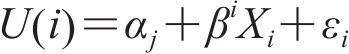
其中αi是与选项相关的常量,βi是由选项i所对应的属性系数构成的向量,Xi是选项i的属性向量,εi是误差项。
准备:需要安装好Python Biogeme包。
步骤:Python Biogeme的语法和Python本身的很像。对于Biogeme而言,Python只是一层很薄的包装,里面还是C++代码(MNL目录中的dcm_mnl.py文件)。下面的代码经过删减了:
1 from biogeme import * 2 from headers import * 3 from loglikelihood import * 4 from statistics import * 5 6 # Specify parameters to be estimated 7 # 8 # Arguments: 9 # - 1 Name, typically, the same as the variable. 10 # - 2 Starting value. 11 # - 3 Lower bound. 12 # - 4 Upper bound. 13 # - 5 flag whether to estimate the parameter (0) 14 # or keep it fixed (1). 15 16 # add the coefficients to be estimated 17 18 ASC = Beta('ASC',0,-10,10,1,'ASC') 19 C_price = Beta('C_price',0,-10,10,0,'C price') 20 Z_price = Beta('Z_price',0,-10,10,0,'Z price') 21 Y_price = Beta('Y_price',0,-10,10,0,'Y price') 22 V_price = Beta('V_price',0,-10,10,0,'V price') 23 24 B_comp = Beta('B_comp',0,-10,10,0,'compartment') 25 B_refund = Beta('B_refund',0,-3,3,0,'refund') 26 27 # Utility functions 28 29 # compartment attributes 30 c = {} 31 32 c[1] = AA777_1_C_compartment 33 c[2] = AA777_2_Z_compartment 34 c[3] = AA777_3_Y_compartment 35 ... 36 c[13] = UA110_1_C_compartment 37 c[14] = UA110_2_Z_compartment 38 c[15] = UA110_3_Y_compartment 39 c[16] = UA110_4_V_compartment 40 41 # price attributes 42 p = {} 43 44 p[1] = AA777_1_C_price 45 p[2] = AA777_2_Z_price 46 p[3] = AA777_3_Y_price 47 ... 48 p[14] = UA110_2_Z_price 49 p[15] = UA110_3_Y_price 50 p[16] = UA110_4_V_price 51 52 # refund attributes 53 r = {} 54 55 r[1] = AA777_1_C_refund 56 r[2] = AA777_2_Z_refund 57 r[3] = AA777_3_Y_refund 58 ... 59 r[13] = UA110_1_C_refund 60 r[14] = UA110_2_Z_refund 61 r[15] = UA110_3_Y_refund 62 r[16] = UA110_4_V_refund 63 64 # The dictionary of utilities is constructed. 65 V = {} 66 67 V[1] = C_price * p[1] + B_refund * r[1] + B_comp * c[1] 68 V[2] = Z_price * p[2] + B_refund * r[2] + B_comp * c[2] + ASC 69 V[3] = Y_price * p[3] + B_refund * r[3] + B_comp * c[3] 70 ... 71 V[13] = C_price * p[13] + B_refund * r[13] + B_comp * c[13] 72 V[14] = Z_price * p[14] + B_refund * r[14] + B_comp * c[14] 73 V[15] = Y_price * p[15] + B_refund * r[15] + B_comp * c[15] 74 V[16] = Y_price * p[16] + B_refund * r[16] + B_comp * c[16] 75 76 # availability flags 77 availability = { 78 1: AA777_1_C_AV, 79 2: AA777_2_Z_AV, 80 3: AA777_3_Y_AV, 81 4: AA777_4_V_AV, 82 5: AS666_1_C_AV, 83 6: AS666_2_Z_AV, 84 7: AS666_3_Y_AV, 85 8: AS666_4_V_AV, 86 9: DL001_1_C_AV, 87 10: DL001_2_Z_AV, 88 11: DL001_3_Y_AV, 89 12: DL001_4_V_AV, 90 13: UA110_1_C_AV, 91 14: UA110_2_Z_AV, 92 15: UA110_3_Y_AV, 93 16: UA110_4_V_AV 94 } 95 96 # The choice model is a logit, with availability conditions 97 logprob = bioLogLogit(V, availability, choice) 98 99 # Defines an iterator on the data 100 rowIterator('obsIter') 101 102 # Define the likelihood function for the estimation 103 BIOGEME_OBJECT.ESTIMATE = Sum(logprob, 'obsIter') 104 105 # Statistics 106 nullLoglikelihood(availability,'obsIter') 107 choiceSet = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16] 108 cteLoglikelihood(choiceSet, choice, 'obsIter') 109 availabilityStatistics(availability, 'obsIter') 110 111 # Parameters 112 BIOGEME_OBJECT.PARAMETERS['optimizationAlgorithm'] = 'BIO' 113 BIOGEME_OBJECT.PARAMETERS['numberOfThreads'] = '8' 114 115 BIOGEME_OBJECT.FORMULAS['AA777 C utility'] = V[1] 116 BIOGEME_OBJECT.FORMULAS['AA777 Z utility'] = V[2] 117 ... 118 BIOGEME_OBJECT.FORMULAS['DL001 Y utility'] = V[11] 119 BIOGEME_OBJECT.FORMULAS['DL001 V utility'] = V[12] 120 BIOGEME_OBJECT.FORMULAS['UA110 C utility'] = V[13] 121 BIOGEME_OBJECT.FORMULAS['UA110 Z utility'] = V[14] 122 BIOGEME_OBJECT.FORMULAS['UA110 Y utility'] = V[15] 123 BIOGEME_OBJECT.FORMULAS['UA110 V utility'] = V[16]
原理:要执行代码,可以使用本章主目录下的run_pythonbiogeme.sh脚本,或者(假设你在MNL目录)执行下面这行:
/* d: cd D:\Java2018\practicalDataAnalysis\Codes\Chapter10\MNL D:\tools\Python37\python D:\tools\Python37\Lib\site-packages\biogeme\biogeme.py dcm_mnl ../../../Data/Chapter10/choices.dat biogeme.py dcm_mnl ../../../Data/Chapter10/choices.dat import os >>> os.chdir('D:\Java2018\practicalDataAnalysis\Codes\Chapter10\MNL') os.getcwd() pythonbiogeme dcm_mnl ../../../Chapter10/choices.dat import os os.chdir('D:\Java2018\practicalDataAnalysis\Codes\Chapter10\MNL') os.getcwd() 'D:\\Java2018\\practicalDataAnalysis\\Codes\\Chapter10\\MNL' >>> biogeme dcm_mnl ../../../Chapter10/choices.dat SyntaxError: invalid syntax >>> biogeme dcm_mnl ../../../Chapter10/choices.dat SyntaxError: invalid syntax pip install biogeme --no-cache-dir import biogeme.version as ver print(ver.getText()) biogeme 3.2.3 [September 25, 2019] Version entirely written in Python Home page: http://biogeme.epfl.ch Submit questions to https://groups.google.com/d/forum/biogeme Michel Bierlaire, Transport and Mobility Laboratory, Ecole Polytechnique Fédérale de Lausanne (EPFL) */
run_pythonbiogeme.sh先清除pythonbiogeme之前生成的文件,再重新估算模型。
使用run_pythonbiogeme.sh脚本也很简单(简单一行命令):
/* ../run_pythonbiogeme.sh dcm_mnl ../../../Data/Chapter10/choices.dat */
随便哪种方式,你都会看到类似下面的内容:
执行不了!!后面再研究。
Init.Log-likelihood给出了log-likelihood函数的初始值,即在初始系数下log-likelihood函数的值。每个选项被选中的可能性都一样。这个值后面会用来计算rho平方值——这个指标等价于线性回归中的R2。估算DCM的目标是最小化log-likelihood函数的绝对值。然后,输出的表展示了估算的进度;你可以看到f(x)(log-likelihood函数)的值越来越小,一直到第7次循环终止,因为第6次循环和第7次循环之间的差足够小了,所以函数收敛了。表下面输出了估算参数的值,不过我们后面会在dcm_mnl.html文件中查看。
现在仔细考察模型文件。
照例,先加载需要的模块。biogeme、headers、log-likelihood以及statistics这几个模块几乎是所有模块都需要的。
然后用Beta(...)方法指定系数。这个方法的第一个参数是参数名(一般情况下,就是对象名)。第二个参数指定了系数的初始值。第三个参数和第四个参数决定了系数值的下界和上界,第五个参数指定系数值是要固定(不估算)还是估算。
对于可识别的模型,要归一化一个参数,即固定为0。通常,这个参数是ASC(alternative specific constants,方案特定变量)中的一个。参考K.Train《Properties of Discrete Choice Models》一书的第2章http://eml.berkeley.edu/books/choice2nd/Ch02_p9-33.pdf。
Beta(...)方法最后一个参数是将要用于报告中的易记名字。
指定了系数后,创建属性名的字典。
这些名字必须同.dat文件中完全相同。
为每个选项指定效用函数时,只使用compartment、price和refund属性。注意,为了避免混淆,存储同一选项的属性时,字典中用的都是同一个数字。
最终,字典V里有全部的效用函数。只对选项2(AA777航班,Z舱位)加进了ASC。也要注意到,B_refund系数和B_comp系数不是选项特定的,而是通用的——所有选项都相同。不同航班之间,等价舱位的价格系数是共用的。
availability对象对每个选项,指定了可用性的标志。
最后,要估算参数,先指定logprob对象。使用bioLogLogit(...)方法估算MNL。这个方法以效用的字典作为第一个参数,可用性的字典作为第二个参数,以及存储choice的变量名。然后在数据集上定义一个迭代器,命名为obsIter。为BIOGEME_OBJECT指定ESTIMATE变量:这是要最小化整个数据集的对数概率和。
剩下的部分就是处理估算的统计数据。nullLogLikelihood(...)方法计算空的log-likelihood并将其包括在输出中。第一个参数是每个选项可用性的字典,第二个参数是行迭代器的名字。cteLoglikelihood(...)计算只有常数参数时log-likelihood函数的值。它以choiceSet(所有选项的列表)作为第一个参数,存储选择的变量名作为第二个参数,记录的迭代器作为第三个参数。得到的统计数据是availabilityStatistics(...),将返回数据集中每个可用选项的起算时间。
最后指定BIOGEME_OBJECT.PARAMETERS和.FORMULAS。使用.PARAMETERS(...)方法,可以向Biogeme及其solver传入各种参数;这里,使用BIO优化器(这是Biogeme自己的优化算法),并指定执行时启动的线程数。.FORMULAS(...)允许我们给效用函数起一个易记名字,并在最终的报告中使用。
Python Biogeme给出的报告如下(删减版;完整版可在浏览器中访问dcm_mnl.html查看):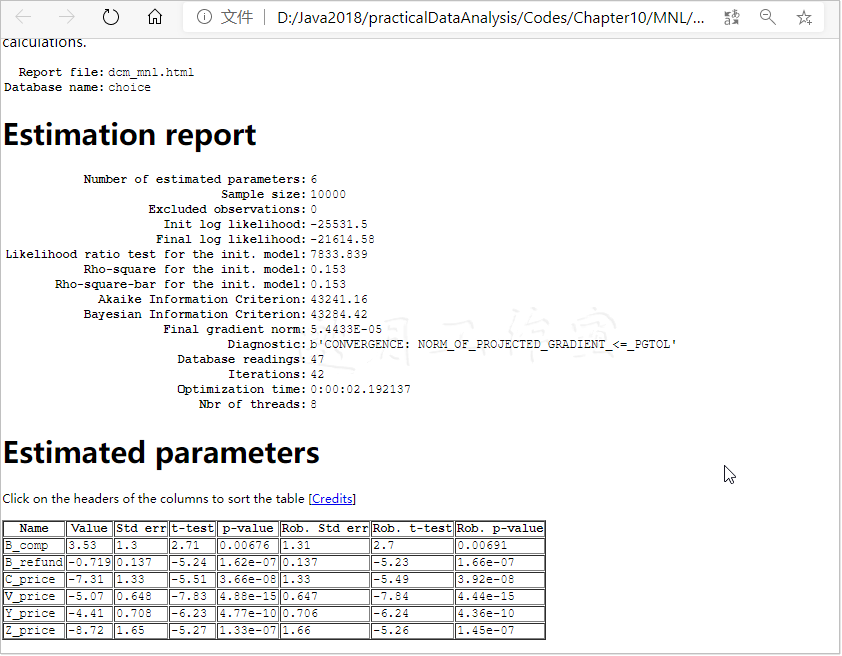
报告给出了多项统计数据。有些已介绍过了,这里就不再重复。看一下init.模型数据的Rho-square-bar:这个数据告诉你,模型表现如何。0.20以上的值就非常好(相当于线性模型中85%的R2),0.15到0.2之间的值不错,0.1到0.15之间的值是可接受的,而不到0.1就是很差的模型了。
重点是,Diagnostic要看Convergence reached。后面我们会看到,Run time也是一项重要数据,尤其是在处理复杂模型时。
考虑Estimated的参数,你需要保留统计上显著(p-values<0.05)的变量。模型中,参数都是统计上显著的。而且,所有价格系数都是负的,意味着更高的价格将降低选中的可能性。意外的是,如果提供一个商务舱的选项,它被选中的可能性就上升了。
参考:
关于MNL,可以参考:
·Kenneth Train的一本(免费)好书:http://eml.berkeley.edu/books/choice2.html;
·一份演示文稿:http://www.bauer.uh.edu/rsusmel/phd/ec1-20.pdf;
·Python Biogeme的介绍:http://biogeme.epfl.ch/documentation/pythonfirstmodel-2.4.pdf。
10.4
测试来自无关选项的独立性冲突
MNL基于一个相当严格的IIA假设,选项的概率之间的比率保持不变。这其实只适用于选项集合没有共同特征的情况,换种说法就是,选项之间不相关。
最著名的IIA反例就是红蓝大巴悖论。考虑这样的场景,你要在汽车、火车、蓝色大巴之间做选择。简化一下,假设每个选项的概率都是1/3。在IIA假设下,如果加入一个红色大巴的选项,选项概率之间的比率恒定,所以各选项的概率都成了1/4。
然而,现实中,颜色因素会有这么大的影响?如果没有,我们实际上还是在汽车、火车、大巴之间做选择。加入一个新的大巴选项,不该影响汽车和火车的概率,其还应该是1/3。而红色与蓝色的概率对半分,两个大巴选项的概率应该都是1/6。
这就违反了IIA假设:P(car)/P(train)没变,P(car)/P(blue bus)和P(train)/P(blue bus)都变了。
本技巧中,我们会考察数据集中是否违反了IIA。下两项技巧中,我们将提供能处理选项之间相关性的模型。
准备:需要安装好Python Biogeme包。
步骤:前一技巧中估算了MNL模型,我们来计算各选项的概率。然后移除第一个选项,重新估算模型,再对新模型重新计算。最后比较概率之间的比率。本技巧用到的文件在TestingIIA目录下。
代码和估算的差不多,所以只讨论不同的地方(TestingIIA/dcm_mnl_simul.py文件):
1 from biogeme import * 2 from headers import * 3 from loglikelihood import * 4 from statistics import * 5 6 # Specify parameters to be estimated 7 # 8 # Arguments: 9 # - 1 Name, typically, the same as the variable. 10 # - 2 Starting value. 11 # - 3 Lower bound. 12 # - 4 Upper bound. 13 # - 5 flag whether to estimate the parameter (0) 14 # or keep it fixed (1). 15 16 # add the coefficients to be estimated 17 C_price = Beta('C_price',-7.29885,-10,10,0,'C price' ) 18 V_price = Beta('V_price',-5.07495,-10,10,0,'V price' ) 19 Y_price = Beta('Y_price',-4.40754,-10,10,0,'Y price' ) 20 Z_price = Beta('Z_price',-8.70638,-10,10,0,'Z price' ) 21 22 ASC = Beta('ASC',0,-10,10,1,'ASC' ) 23 B_comp = Beta('B_comp',3.52571,-10,10,0,'compartment' ) 24 B_refund = Beta('B_refund',-0.718748,-3,3,0,'refund' ) 25 26 # Utility functions 27 28 # The data are associated with the alternative index 29 # compartment attributes 30 c = {} 31 32 c[1] = AA777_1_C_compartment 33 c[2] = AA777_2_Z_compartment 34 c[3] = AA777_3_Y_compartment 35 c[4] = AA777_4_V_compartment 36 c[5] = AS666_1_C_compartment 37 c[6] = AS666_2_Z_compartment 38 c[7] = AS666_3_Y_compartment 39 c[8] = AS666_4_V_compartment 40 c[9] = DL001_1_C_compartment 41 c[10] = DL001_2_Z_compartment 42 c[11] = DL001_3_Y_compartment 43 c[12] = DL001_4_V_compartment 44 c[13] = UA110_1_C_compartment 45 c[14] = UA110_2_Z_compartment 46 c[15] = UA110_3_Y_compartment 47 c[16] = UA110_4_V_compartment 48 49 # price attributes 50 p = {} 51 52 p[1] = AA777_1_C_price 53 p[2] = AA777_2_Z_price 54 p[3] = AA777_3_Y_price 55 p[4] = AA777_4_V_price 56 p[5] = AS666_1_C_price 57 p[6] = AS666_2_Z_price 58 p[7] = AS666_3_Y_price 59 p[8] = AS666_4_V_price 60 p[9] = DL001_1_C_price 61 p[10] = DL001_2_Z_price 62 p[11] = DL001_3_Y_price 63 p[12] = DL001_4_V_price 64 p[13] = UA110_1_C_price 65 p[14] = UA110_2_Z_price 66 p[15] = UA110_3_Y_price 67 p[16] = UA110_4_V_price 68 69 # refund attributes 70 r = {} 71 72 r[1] = AA777_1_C_refund 73 r[2] = AA777_2_Z_refund 74 r[3] = AA777_3_Y_refund 75 r[4] = AA777_4_V_refund 76 r[5] = AS666_1_C_refund 77 r[6] = AS666_2_Z_refund 78 r[7] = AS666_3_Y_refund 79 r[8] = AS666_4_V_refund 80 r[9] = DL001_1_C_refund 81 r[10] = DL001_2_Z_refund 82 r[11] = DL001_3_Y_refund 83 r[12] = DL001_4_V_refund 84 r[13] = UA110_1_C_refund 85 r[14] = UA110_2_Z_refund 86 r[15] = UA110_3_Y_refund 87 r[16] = UA110_4_V_refund 88 89 # The dictionary of utilities is constructed. 90 V = {} 91 92 V[1] = C_price * p[1] + B_refund * r[1] + B_comp * c[1] 93 V[2] = Z_price * p[2] + B_refund * r[2] + B_comp * c[2] + ASC 94 V[3] = Y_price * p[3] + B_refund * r[3] + B_comp * c[3] 95 V[4] = V_price * p[4] + B_refund * r[4] + B_comp * c[4] 96 V[5] = C_price * p[5] + B_refund * r[5] + B_comp * c[5] 97 V[6] = Z_price * p[6] + B_refund * r[6] + B_comp * c[6] 98 V[7] = Y_price * p[7] + B_refund * r[7] + B_comp * c[7] 99 V[8] = V_price * p[8] + B_refund * r[8] + B_comp * c[8] 100 V[9] = C_price * p[9] + B_refund * r[9] + B_comp * c[9] 101 V[10] = Z_price * p[10] + B_refund * r[10] + B_comp * c[10] 102 V[11] = Y_price * p[11] + B_refund * r[11] + B_comp * c[11] 103 V[12] = V_price * p[12] + B_refund * r[12] + B_comp * c[12] 104 V[13] = C_price * p[13] + B_refund * r[13] + B_comp * c[13] 105 V[14] = Z_price * p[14] + B_refund * r[14] + B_comp * c[14] 106 V[15] = Y_price * p[15] + B_refund * r[15] + B_comp * c[15] 107 V[16] = Y_price * p[16] + B_refund * r[16] + B_comp * c[16] 108 109 # availability flags 110 availability = { 111 1: AA777_1_C_AV, 112 2: AA777_2_Z_AV, 113 3: AA777_3_Y_AV, 114 4: AA777_4_V_AV, 115 5: AS666_1_C_AV, 116 6: AS666_2_Z_AV, 117 7: AS666_3_Y_AV, 118 8: AS666_4_V_AV, 119 9: DL001_1_C_AV, 120 10: DL001_2_Z_AV, 121 11: DL001_3_Y_AV, 122 12: DL001_4_V_AV, 123 13: UA110_1_C_AV, 124 14: UA110_2_Z_AV, 125 15: UA110_3_Y_AV, 126 16: UA110_4_V_AV 127 } 128 129 # The choice model is a logit, with availability conditions 130 probAA777_C = bioLogit(V, availability, 1) 131 probAA777_Z = bioLogit(V, availability, 2) 132 probAA777_Y = bioLogit(V, availability, 3) 133 probAA777_V = bioLogit(V, availability, 4) 134 probAS666_C = bioLogit(V, availability, 5) 135 probAS666_Z = bioLogit(V, availability, 6) 136 probAS666_Y = bioLogit(V, availability, 7) 137 probAS666_V = bioLogit(V, availability, 8) 138 probDL001_C = bioLogit(V, availability, 9) 139 probDL001_Z = bioLogit(V, availability, 10) 140 probDL001_Y = bioLogit(V, availability, 11) 141 probDL001_V = bioLogit(V, availability, 12) 142 probUA110_C = bioLogit(V, availability, 13) 143 probUA110_Z = bioLogit(V, availability, 14) 144 probUA110_Y = bioLogit(V, availability, 15) 145 probUA110_V = bioLogit(V, availability, 16) 146 147 # Defines an itertor on the data 148 rowIterator('obsIter') 149 150 # exclude observations where AA777 C was selected 151 exclude = choice == 1 152 BIOGEME_OBJECT.EXCLUDE = exclude 153 154 # simulate 155 simulate = { 156 'P_AA777_C': probAA777_C, 157 'P_AA777_Z': probAA777_Z, 158 'P_AA777_Y': probAA777_Y, 159 'P_AA777_V': probAA777_V, 160 'P_AS666_C': probAS666_C, 161 'P_AS666_Z': probAS666_Z, 162 'P_AS666_Y': probAS666_Y, 163 'P_AS666_V': probAS666_V, 164 'P_DL001_C': probDL001_C, 165 'P_DL001_Z': probDL001_Z, 166 'P_DL001_Y': probDL001_Y, 167 'P_DL001_V': probDL001_V, 168 'P_UA110_C': probUA110_C, 169 'P_UA110_Z': probUA110_Z, 170 'P_UA110_Y': probUA110_Y, 171 'P_UA110_V': probUA110_V 172 } 173 174 ## Code for the sensitivity analysis 175 names = ['B_comp','B_refund','C_price','V_price','Y_price','Z_price'] 176 values = [[1.71083,-0.0398667,-1.67587,0.190499,0.209566,-2.13821],[-0.0398667,0.0188657,-0.00717013,-0.083915,-0.0941582,0.0155518],[-1.67587,-0.00717013,1.76813,0.0330621,0.0365816,2.18927],[0.190499,-0.083915,0.0330621,0.418485,0.452985,-0.0676863],[0.209566,-0.0941582,0.0365816,0.452985,0.498726,-0.0766095],[-2.13821,0.0155518,2.18927,-0.0676863,-0.0766095,2.74714]] 177 vc = bioMatrix(6, names, values) 178 BIOGEME_OBJECT.VARCOVAR = vc 179 180 BIOGEME_OBJECT.SIMULATE = Enumerate(simulate,'obsIter') 181 182 # Statistics 183 nullLoglikelihood(availability,'obsIter') 184 choiceSet = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16] 185 cteLoglikelihood(choiceSet, choice, 'obsIter') 186 availabilityStatistics(availability, 'obsIter') 187 188 # Parameters 189 BIOGEME_OBJECT.PARAMETERS['RandomDistribution'] ="MLHS" 190 BIOGEME_OBJECT.PARAMETERS['NbrOfDraws'] = "1" 191 192 BIOGEME_OBJECT.FORMULAS['AA777 C utility'] = V[1] 193 BIOGEME_OBJECT.FORMULAS['AA777 Z utility'] = V[2] 194 BIOGEME_OBJECT.FORMULAS['AA777 Y utility'] = V[3] 195 BIOGEME_OBJECT.FORMULAS['AA777 V utility'] = V[4] 196 BIOGEME_OBJECT.FORMULAS['AS666 C utility'] = V[5] 197 BIOGEME_OBJECT.FORMULAS['AS666 Z utility'] = V[6] 198 BIOGEME_OBJECT.FORMULAS['AS666 Y utility'] = V[7] 199 BIOGEME_OBJECT.FORMULAS['AS666 V utility'] = V[8] 200 BIOGEME_OBJECT.FORMULAS['DL001 C utility'] = V[9] 201 BIOGEME_OBJECT.FORMULAS['DL001 Z utility'] = V[10] 202 BIOGEME_OBJECT.FORMULAS['DL001 Y utility'] = V[11] 203 BIOGEME_OBJECT.FORMULAS['DL001 V utility'] = V[12] 204 BIOGEME_OBJECT.FORMULAS['UA110 C utility'] = V[13] 205 BIOGEME_OBJECT.FORMULAS['UA110 Z utility'] = V[14] 206 BIOGEME_OBJECT.FORMULAS['UA110 Y utility'] = V[15] 207 BIOGEME_OBJECT.FORMULAS['UA110 V utility'] = V[16]
原理:和估算模型一样,先加载Python Biogeme使用的包。
然后定义系数。然而,使用已估算的系数。其可从MNL文件夹下的dcm_mnl_param.py文件导入。接着,指定属性和效用的字典。
在IIA测试中,将排除AA777_C选项,移除完整的模型中选择这个选项的所有观测值。你只要指定条件——这里是choice==1——并设置BIOGEME_OBJECT的.EXCLUDE变量。
当然,条件也可能非常复杂。
决定了可用性和排除项后,我们用biologit(...)方法为每个概率创建一个变量,放到模拟的字典中。这个方法以效用的字典作为第一个参数,以可用性的字典作为第二个参数。最后一个参数指定了选项的序数。
最后,我们指定系数的名字和系数的协方差矩阵。这也可从MNL文件夹下的dcm_mnl_param.py文件导入。Python Biogeme将会在敏感度分析中使用。
使用Enumerate(...)方法仿真概率。这个方法以模拟的字典作为第一个参数,以行迭代器作为第二个参数。由于我们只对概率的估算感兴趣(而不是蒙特卡洛分析),我们将RandomDistribution指定为MLHS(Modified Latin Hypercube Sampling,修正拉丁超立方抽样),只画一次。
和估算一样运行模拟,输入一行命令:
/*
../run_pythonbiogeme.sh dcm_mnl_simul ../../../Data/Chapter10/choices.dat
*/
同样报错!
软件包创建了dcm_mnl_simul.html,包含计算出的概率表格,如下图所示: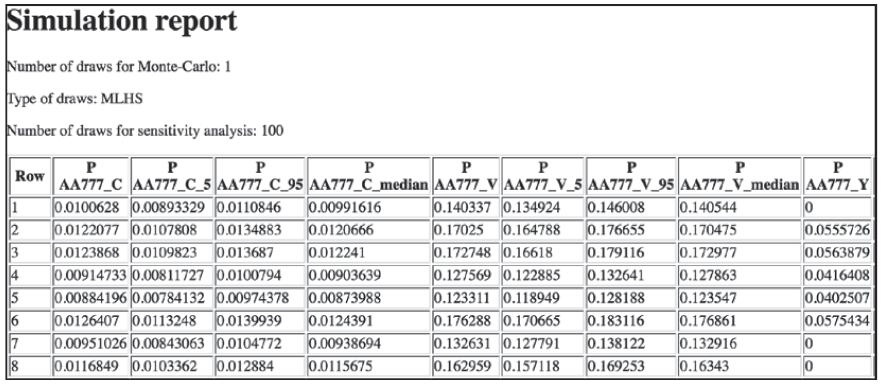
表格有10000行。对于敏感度分析,仿真过程画出了100个均匀分布的系数参数,返回每个选项的第5个、第95个以及中位数。
最后一步,我们移除第一个选项,重复模拟的过程(TestingIIA目录下的dcm_iia.py文件和dcm_iia_simul.py文件):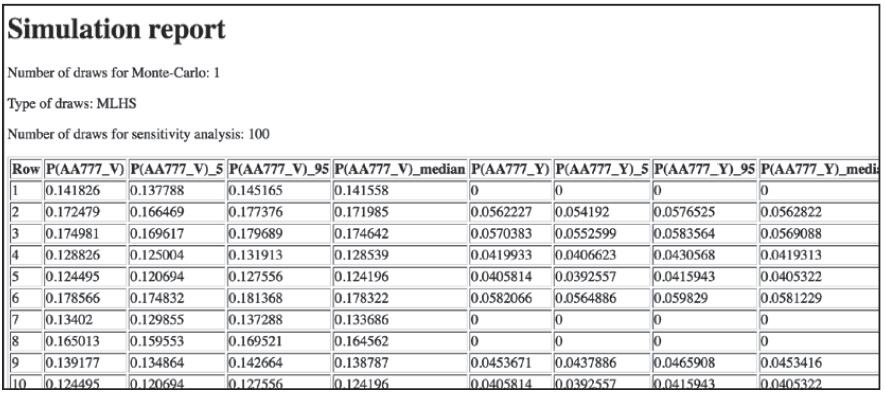
可以看到,AA777_C选项不在了。如果满足IIA的要求,我们看到的概率应该不变。我们分析下第二行。
原始模型的P(AA777_V)是0.17025,P(AA777_Y)是0.0555726;比率是3.0636。新模型中,P(AA777_V)=0.172479,P(AA777_Y)=0.0562227;新比率是3.0678。
变化不大。
更多:
然而,这只是一个观测值。我们检查一下其余选项(dcm_iia_testing.py文件):
1 import pandas as pd 2 3 # read the html tables 4 old_model = 'dcm_mnl_simul.html' 5 new_model = 'dcm_iia_simul.html' 6 7 old_model_p = pd.read_html(old_model, header = 0)[3] 8 new_model_p = pd.read_html(new_model, header = 0)[3] 9 10 # let's look at only two columns 11 cols = ['P_AA777_Y', 'P_AA777_V'] 12 13 # make sure that there are no zeros 14 old_model_p = old_model_p[cols] 15 old_model_p = old_model_p[old_model_p[cols[0]] != 0] 16 old_model_p = old_model_p[old_model_p[cols[1]] != 0] 17 18 new_model_p = new_model_p[cols] 19 new_model_p = new_model_p[new_model_p[cols[0]] != 0] 20 new_model_p = new_model_p[new_model_p[cols[1]] != 0] 21 22 # calculate the ratios 23 old_model_p['ratios_old'] = old_model_p \ 24 .apply(lambda row: row['P_AA777_V'] / row['P_AA777_Y'], 25 axis=1) 26 27 new_model_p['ratios_new'] = new_model_p \ 28 .apply(lambda row: row['P_AA777_V'] / row['P_AA777_Y'], 29 axis=1) 30 31 # join with the old model results 32 differences = old_model_p.join(new_model_p, rsuffix='_new') 33 34 # and calculate the differences 35 differences['diff'] = differences\ 36 .apply(lambda row: row['ratios_new'] - row['ratios_old'], 37 axis=1) 38 39 # calculate the descriptive stats for the columns 40 print(differences[['ratios_old', 'ratios_new', 'diff']] \ 41 .describe())
我们使用pandas,因为它提供了从HTML文件直接读取表格的方法(参考本书1.6节)。
读入了文件,我们从完整模型和精简模型中读取之前测试过的两列,确保列中没有0。然后,计算比率并连接两个文件以计算差异。最后,我们生成描述性统计数据: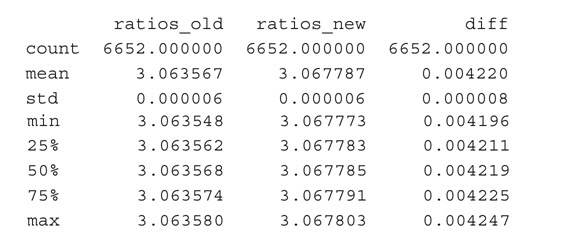
差变化不大——变异系数(标准差/平均值)接近于0,最大的差是0.004247。所以,我们不能说违反了IIA。
10.5用巢式Logit模型处理IIA冲突
不过,如果你的模型违反了IIA,那么你就得使用更高级的模型。本技巧中,我们将认识一个稍微复杂点的巢式Logit模型。这个模型将相似的选项放到一个巢里(名字的由来)。篇幅有限,我们这里不讨论模型的原理,但是我极力推荐之前提过的Kenneth Train的书。
准备:需要装好Python Biogeme包。
步骤:
模型代码的框架还是一样的;这里,我们只展示不同之处(Nested/dcm_nested.py文件):
1 from biogeme import * 2 from headers import * 3 from nested import * 4 from loglikelihood import * 5 from statistics import * 6 7 # Specify parameters to be estimated 8 # 9 # Arguments: 10 # - 1 Name, typically, the same as the variable. 11 # - 2 Starting value. 12 # - 3 Lower bound. 13 # - 4 Upper bound. 14 # - 5 flag whether to estimate the parameter (0) 15 # or keep it fixed (1). 16 17 # add the coefficients to be estimated 18 C_price = Beta('C_price',0,-10,10,0,'C price' ) 19 V_price = Beta('V_price',0,-10,10,0,'V price' ) 20 Y_price = Beta('Y_price',0,-10,10,0,'Y price' ) 21 Z_price = Beta('Z_price',0,-10,10,0,'Z price' ) 22 23 ASC = Beta('ASC',0,-10,10,1,'ASC' ) 24 25 B_refund = Beta('B_refund',0,-3,3,0,'refund' ) 26 B_comp = Beta('B_comp',0,-3,3,0,'compartment' ) 27 28 # nest mu parameter 29 biz_mu = Beta('biz_mu',0.5,0,1,0) 30 eco_mu = Beta('eco_mu',0.5,0,1,0) 31 32 # Utility functions 33 34 # compartment attributes 35 c = {} 36 37 c[1] = AA777_1_C_compartment 38 c[2] = AA777_2_Z_compartment 39 c[3] = AA777_3_Y_compartment 40 c[4] = AA777_4_V_compartment 41 c[5] = AS666_1_C_compartment 42 c[6] = AS666_2_Z_compartment 43 c[7] = AS666_3_Y_compartment 44 c[8] = AS666_4_V_compartment 45 c[9] = DL001_1_C_compartment 46 c[10] = DL001_2_Z_compartment 47 c[11] = DL001_3_Y_compartment 48 c[12] = DL001_4_V_compartment 49 c[13] = UA110_1_C_compartment 50 c[14] = UA110_2_Z_compartment 51 c[15] = UA110_3_Y_compartment 52 c[16] = UA110_4_V_compartment 53 54 # price attributes 55 p = {} 56 57 p[1] = AA777_1_C_price 58 p[2] = AA777_2_Z_price 59 p[3] = AA777_3_Y_price 60 p[4] = AA777_4_V_price 61 p[5] = AS666_1_C_price 62 p[6] = AS666_2_Z_price 63 p[7] = AS666_3_Y_price 64 p[8] = AS666_4_V_price 65 p[9] = DL001_1_C_price 66 p[10] = DL001_2_Z_price 67 p[11] = DL001_3_Y_price 68 p[12] = DL001_4_V_price 69 p[13] = UA110_1_C_price 70 p[14] = UA110_2_Z_price 71 p[15] = UA110_3_Y_price 72 p[16] = UA110_4_V_price 73 74 # refund attributes 75 r = {} 76 77 r[1] = AA777_1_C_refund 78 r[2] = AA777_2_Z_refund 79 r[3] = AA777_3_Y_refund 80 r[4] = AA777_4_V_refund 81 r[5] = AS666_1_C_refund 82 r[6] = AS666_2_Z_refund 83 r[7] = AS666_3_Y_refund 84 r[8] = AS666_4_V_refund 85 r[9] = DL001_1_C_refund 86 r[10] = DL001_2_Z_refund 87 r[11] = DL001_3_Y_refund 88 r[12] = DL001_4_V_refund 89 r[13] = UA110_1_C_refund 90 r[14] = UA110_2_Z_refund 91 r[15] = UA110_3_Y_refund 92 r[16] = UA110_4_V_refund 93 94 # The dictionary of utilities is constructed. 95 V = {} 96 97 V[1] = Z_price * p[1] + B_refund * r[1] + B_comp * c[1] 98 V[2] = Z_price * p[2] + B_refund * r[2] + B_comp * c[2] + ASC 99 V[3] = Y_price * p[3] + B_refund * r[3] + B_comp * c[3] 100 V[4] = V_price * p[4] + B_refund * r[4] + B_comp * c[4] 101 V[5] = C_price * p[5] + B_refund * r[5] + B_comp * c[5] 102 V[6] = Z_price * p[6] + B_refund * r[6] + B_comp * c[6] 103 V[7] = Y_price * p[7] + B_refund * r[7] + B_comp * c[7] 104 V[8] = V_price * p[8] + B_refund * r[8] + B_comp * c[8] 105 V[9] = C_price * p[9] + B_refund * r[9] + B_comp * c[9] 106 V[10] = Z_price * p[10] + B_refund * r[10] + B_comp * c[10] 107 V[11] = Y_price * p[11] + B_refund * r[11] + B_comp * c[11] 108 V[12] = V_price * p[12] + B_refund * r[12] + B_comp * c[12] 109 V[13] = C_price * p[13] + B_refund * r[13] + B_comp * c[13] 110 V[14] = Z_price * p[14] + B_refund * r[14] + B_comp * c[14] 111 V[15] = Y_price * p[15] + B_refund * r[15] + B_comp * c[15] 112 V[16] = Y_price * p[16] + B_refund * r[16] + B_comp * c[16] 113 114 # availability flags 115 availability = { 116 1: AA777_1_C_AV, 117 2: AA777_2_Z_AV, 118 3: AA777_3_Y_AV, 119 4: AA777_4_V_AV, 120 5: AS666_1_C_AV, 121 6: AS666_2_Z_AV, 122 7: AS666_3_Y_AV, 123 8: AS666_4_V_AV, 124 9: DL001_1_C_AV, 125 10: DL001_2_Z_AV, 126 11: DL001_3_Y_AV, 127 12: DL001_4_V_AV, 128 13: UA110_1_C_AV, 129 14: UA110_2_Z_AV, 130 15: UA110_3_Y_AV, 131 16: UA110_4_V_AV 132 } 133 134 # 1: nests parameter 135 # 2: list of alternatives 136 business = biz_mu, [1,2,5,6,9,10,13,14] 137 economy = eco_mu, [3,4,7,8,11,12,15,16] 138 nests = business, economy 139 140 # The choice model is a logit, with availability conditions 141 logprob = lognested(V, availability, nests, choice) 142 143 # Defines an itertor on the data 144 rowIterator('obsIter') 145 146 # DEfine the likelihood function for the estimation 147 BIOGEME_OBJECT.ESTIMATE = Sum(logprob,'obsIter') 148 149 # Statistics 150 151 nullLoglikelihood(availability,'obsIter') 152 choiceSet = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16] 153 cteLoglikelihood(choiceSet,choice,'obsIter') 154 availabilityStatistics(availability,'obsIter') 155 156 BIOGEME_OBJECT.PARAMETERS['optimizationAlgorithm'] = 'BIO' 157 BIOGEME_OBJECT.PARAMETERS['checkDerivatives'] = '1' 158 BIOGEME_OBJECT.PARAMETERS['numberOfThreads'] = '8' 159 BIOGEME_OBJECT.PARAMETERS['moreRobustToNumericalIssues'] = '0' 160 161 BIOGEME_OBJECT.FORMULAS['AA777 C utility'] = V[1] 162 BIOGEME_OBJECT.FORMULAS['AA777 Z utility'] = V[2] 163 BIOGEME_OBJECT.FORMULAS['AA777 Y utility'] = V[3] 164 BIOGEME_OBJECT.FORMULAS['AA777 V utility'] = V[4] 165 BIOGEME_OBJECT.FORMULAS['AS666 C utility'] = V[5] 166 BIOGEME_OBJECT.FORMULAS['AS666 Z utility'] = V[6] 167 BIOGEME_OBJECT.FORMULAS['AS666 Y utility'] = V[7] 168 BIOGEME_OBJECT.FORMULAS['AS666 V utility'] = V[8] 169 BIOGEME_OBJECT.FORMULAS['DL001 C utility'] = V[9] 170 BIOGEME_OBJECT.FORMULAS['DL001 Z utility'] = V[10] 171 BIOGEME_OBJECT.FORMULAS['DL001 Y utility'] = V[11] 172 BIOGEME_OBJECT.FORMULAS['DL001 V utility'] = V[12] 173 BIOGEME_OBJECT.FORMULAS['UA110 C utility'] = V[13] 174 BIOGEME_OBJECT.FORMULAS['UA110 Z utility'] = V[14] 175 BIOGEME_OBJECT.FORMULAS['UA110 Y utility'] = V[15] 176 BIOGEME_OBJECT.FORMULAS['UA110 V utility'] = V[16]
原理:前面已经指出,MNL和NL的主要差别在于,NL将有共性的选项放在一起。每个巢关联一个lambda参数:这个参数定义了巢中选项间竞争有多激烈。lambda参数取值范围在0(竞争最激烈)和1(没有竞争)之间。
我们的例子中,我们假设商务选项(舱位C和Z)有更大的休息室和更好的服务,所以将他们放到商务巢中;经济选项(舱位Y和V)放到经济巢中。biz_mu和eco_mu是我们巢的lambda参数。
然后我们传入带选项数字的列表以及lambda参数,将选项分配到巢。
我们也要使用一个不同的估算器——lognested(...)方法,而不是bioLogLogit(...)方法;这个额外加入了nests对象: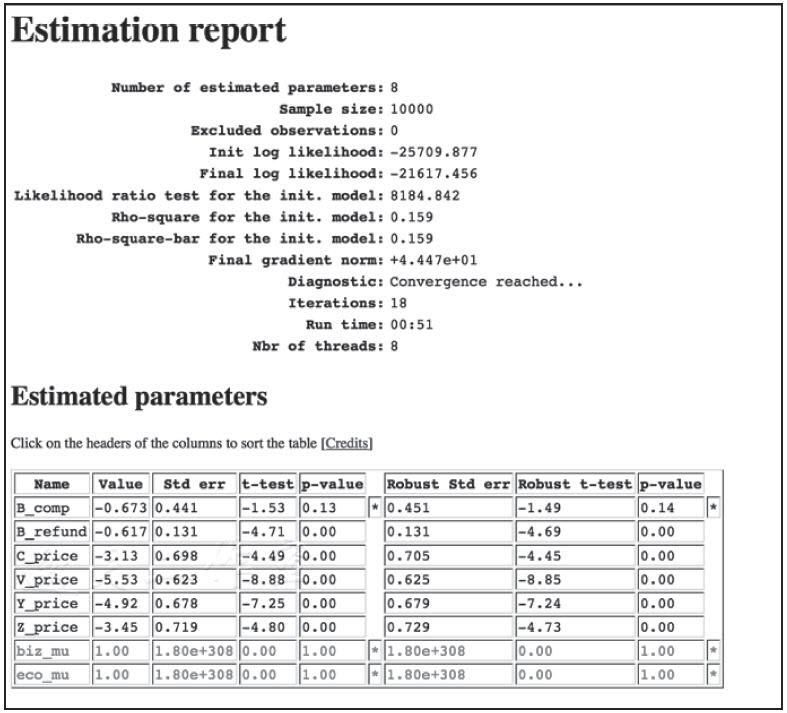
果然,巢的结构并没有给模型带来什么好处。Rho平方值略好一点,但付出的代价是两个额外的自由度。另外,biz_mu和biz_eco也不是统计上显著的。
10.6用混合Logit模型处理复杂的替代模式
混合Logit模型,与前面介绍的模型都不同,允许有些系数随机地服从一个正态分布,也就是说,有均值和标准差。这样的效果是降低了对IIA假设的依赖,也允许灵活地给替代模式建模。不过,这也要付出计算时间的代价。
准备:需要装好Python Biogeme包。
步骤:由于我们已经明确了,用我们的数据集估算出来的MNL模型,并不违反IIA性质,我们就只展示一下估算混合Logit模型的机制(MixedLogit/dcm_mixed.py文件):
1 from biogeme import * 2 from headers import * 3 from loglikelihood import * 4 from statistics import * 5 6 # Specify parameters to be estimated 7 # 8 # Arguments: 9 # - 1 Name, typically, the same as the variable. 10 # - 2 Starting value. 11 # - 3 Lower bound. 12 # - 4 Upper bound. 13 # - 5 flag whether to estimate the parameter (0) 14 # or keep it fixed (1). 15 16 # add the coefficients to be estimated 17 18 C_price = Beta('C_price',0,-10,10,0,'C price' ) 19 V_price = Beta('V_price',0,-10,10,0,'V price' ) 20 Y_price = Beta('Y_price',0,-10,10,0,'Y price' ) 21 Z_price = Beta('Z_price',0,-10,10,0,'Z price' ) 22 23 ASC = Beta('ASC',0,-10,10,1,'ASC' ) 24 25 B_ref = Beta('B_ref',0,-3,3,0,'refund' ) 26 B_ref_S = Beta('B_ref_S',0,-3,3,0,'refund (std)' ) 27 B_comp = Beta('B_comp',0,-3,3,0,'compartment' ) 28 29 # Random parameters 30 B_ref_rnd = B_ref + B_ref_S * bioDraws('B_ref_rnd') 31 32 # Utility functions 33 34 # The data are associated with the alternative index 35 # compartment attributes 36 c = {} 37 38 c[1] = AA777_1_C_compartment 39 c[2] = AA777_2_Z_compartment 40 c[3] = AA777_3_Y_compartment 41 c[4] = AA777_4_V_compartment 42 c[5] = AS666_1_C_compartment 43 c[6] = AS666_2_Z_compartment 44 c[7] = AS666_3_Y_compartment 45 c[8] = AS666_4_V_compartment 46 c[9] = DL001_1_C_compartment 47 c[10] = DL001_2_Z_compartment 48 c[11] = DL001_3_Y_compartment 49 c[12] = DL001_4_V_compartment 50 c[13] = UA110_1_C_compartment 51 c[14] = UA110_2_Z_compartment 52 c[15] = UA110_3_Y_compartment 53 c[16] = UA110_4_V_compartment 54 55 # price attributes 56 p = {} 57 58 p[1] = AA777_1_C_price 59 p[2] = AA777_2_Z_price 60 p[3] = AA777_3_Y_price 61 p[4] = AA777_4_V_price 62 p[5] = AS666_1_C_price 63 p[6] = AS666_2_Z_price 64 p[7] = AS666_3_Y_price 65 p[8] = AS666_4_V_price 66 p[9] = DL001_1_C_price 67 p[10] = DL001_2_Z_price 68 p[11] = DL001_3_Y_price 69 p[12] = DL001_4_V_price 70 p[13] = UA110_1_C_price 71 p[14] = UA110_2_Z_price 72 p[15] = UA110_3_Y_price 73 p[16] = UA110_4_V_price 74 75 # refund attributes 76 r = {} 77 78 r[1] = AA777_1_C_refund 79 r[2] = AA777_2_Z_refund 80 r[3] = AA777_3_Y_refund 81 r[4] = AA777_4_V_refund 82 r[5] = AS666_1_C_refund 83 r[6] = AS666_2_Z_refund 84 r[7] = AS666_3_Y_refund 85 r[8] = AS666_4_V_refund 86 r[9] = DL001_1_C_refund 87 r[10] = DL001_2_Z_refund 88 r[11] = DL001_3_Y_refund 89 r[12] = DL001_4_V_refund 90 r[13] = UA110_1_C_refund 91 r[14] = UA110_2_Z_refund 92 r[15] = UA110_3_Y_refund 93 r[16] = UA110_4_V_refund 94 95 # The dictionary of utilities is constructed. 96 V = {} 97 98 V[1] = Z_price * p[1] + B_ref_rnd * r[1] + B_comp * c[1] 99 V[2] = Z_price * p[2] + B_ref_rnd * r[2] + B_comp * c[2] + ASC 100 V[3] = Y_price * p[3] + B_ref_rnd * r[3] + B_comp * c[3] 101 V[4] = V_price * p[4] + B_ref_rnd * r[4] + B_comp * c[4] 102 V[5] = C_price * p[5] + B_ref_rnd * r[5] + B_comp * c[5] 103 V[6] = Z_price * p[6] + B_ref_rnd * r[6] + B_comp * c[6] 104 V[7] = Y_price * p[7] + B_ref_rnd * r[7] + B_comp * c[7] 105 V[8] = V_price * p[8] + B_ref_rnd * r[8] + B_comp * c[8] 106 V[9] = C_price * p[9] + B_ref_rnd * r[9] + B_comp * c[9] 107 V[10] = Z_price * p[10] + B_ref_rnd * r[10] + B_comp * c[10] 108 V[11] = Y_price * p[11] + B_ref_rnd * r[11] + B_comp * c[11] 109 V[12] = V_price * p[12] + B_ref_rnd * r[12] + B_comp * c[12] 110 V[13] = C_price * p[13] + B_ref_rnd * r[13] + B_comp * c[13] 111 V[14] = Z_price * p[14] + B_ref_rnd * r[14] + B_comp * c[14] 112 V[15] = Y_price * p[15] + B_ref_rnd * r[15] + B_comp * c[15] 113 V[16] = Y_price * p[16] + B_ref_rnd * r[16] + B_comp * c[16] 114 115 # availability flags 116 availability = { 117 1: AA777_1_C_AV, 118 2: AA777_2_Z_AV, 119 3: AA777_3_Y_AV, 120 4: AA777_4_V_AV, 121 5: AS666_1_C_AV, 122 6: AS666_2_Z_AV, 123 7: AS666_3_Y_AV, 124 8: AS666_4_V_AV, 125 9: DL001_1_C_AV, 126 10: DL001_2_Z_AV, 127 11: DL001_3_Y_AV, 128 12: DL001_4_V_AV, 129 13: UA110_1_C_AV, 130 14: UA110_2_Z_AV, 131 15: UA110_3_Y_AV, 132 16: UA110_4_V_AV 133 } 134 135 # The choice model is a logit, with availability conditions 136 prob = bioLogit(V, availability, choice) 137 l = mixedloglikelihood(prob) 138 139 # Defines an itertor on the data 140 rowIterator('obsIter') 141 142 # Define the likelihood function for the estimation 143 BIOGEME_OBJECT.ESTIMATE = Sum(l, 'obsIter') 144 145 # Statistics 146 147 nullLoglikelihood(availability,'obsIter') 148 choiceSet = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16] 149 cteLoglikelihood(choiceSet, choice, 'obsIter') 150 availabilityStatistics(availability, 'obsIter') 151 152 BIOGEME_OBJECT.PARAMETERS['NbrOfDraws'] = '100' 153 BIOGEME_OBJECT.DRAWS = { 'B_ref_rnd': 'NORMAL' } 154 BIOGEME_OBJECT.PARAMETERS['optimizationAlgorithm'] = 'BIO' 155 BIOGEME_OBJECT.PARAMETERS['numberOfThreads'] = '8' 156 157 BIOGEME_OBJECT.FORMULAS['AA777 C utility'] = V[1] 158 BIOGEME_OBJECT.FORMULAS['AA777 Z utility'] = V[2] 159 BIOGEME_OBJECT.FORMULAS['AA777 Y utility'] = V[3] 160 BIOGEME_OBJECT.FORMULAS['AA777 V utility'] = V[4] 161 BIOGEME_OBJECT.FORMULAS['AS666 C utility'] = V[5] 162 BIOGEME_OBJECT.FORMULAS['AS666 Z utility'] = V[6] 163 BIOGEME_OBJECT.FORMULAS['AS666 Y utility'] = V[7] 164 BIOGEME_OBJECT.FORMULAS['AS666 V utility'] = V[8] 165 BIOGEME_OBJECT.FORMULAS['DL001 C utility'] = V[9] 166 BIOGEME_OBJECT.FORMULAS['DL001 Z utility'] = V[10] 167 BIOGEME_OBJECT.FORMULAS['DL001 Y utility'] = V[11] 168 BIOGEME_OBJECT.FORMULAS['DL001 V utility'] = V[12] 169 BIOGEME_OBJECT.FORMULAS['UA110 C utility'] = V[13] 170 BIOGEME_OBJECT.FORMULAS['UA110 Z utility'] = V[14] 171 BIOGEME_OBJECT.FORMULAS['UA110 Y utility'] = V[15] 172 BIOGEME_OBJECT.FORMULAS['UA110 V utility'] = V[16]
原理:随机的B_ref_rnd参数由确定的部分(平均值)B_ref和变化的部分(随机值)B_ref_S——即标准差——组成。
bioDraws(...)用于任意抽选。抽选是针对每一个观测值进行的,这就带来了性能问题:对于每个观测值,估算器都要进行正态分布预定次数的抽样,以估算系数。
之后每个效用函数都使用random参数取代B_ref;这么做可以处理替代模式,因为模型可以在这个维度上处理选项之间的相关性。
mixedloglikelihood(...)方法进行模型的预估。它唯一的参数是bioLogit(...)对象。
设置.DRAWS变量,指定从什么分布中抽;我们的例子里是正态分布。结果如下: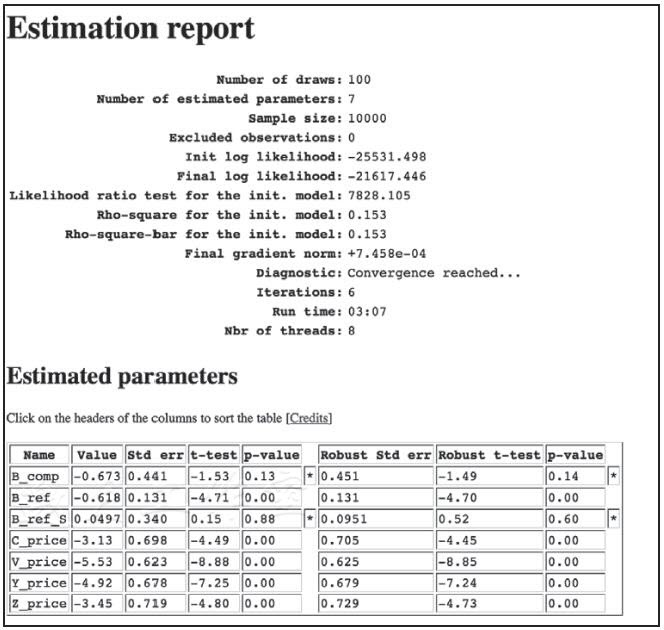
如我们所料,附加的估算系数并没有给模型带来价值;B_ref_S并不显著,完全可以从模型中移除,也不会损失精确度。
同之前的模型相比,你可以发现ML估算的时间比较久:MNL要花1秒,而NL要花50秒。
第10章完。
 托马兹·卓巴斯的《数据分析实战》,2018年6月出版,本系列为读书笔记。主要是为了系统整理,加深记忆。 第10章解释了选择模型理论以及一些流行的模型:多项式Logit模型、嵌套Logit模型以及混合Logit模型。
托马兹·卓巴斯的《数据分析实战》,2018年6月出版,本系列为读书笔记。主要是为了系统整理,加深记忆。 第10章解释了选择模型理论以及一些流行的模型:多项式Logit模型、嵌套Logit模型以及混合Logit模型。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号