看完这个视频我算是明白了正弦余弦是怎么来的了。

傅里叶、拉普拉斯、卷积、欧拉方程、梯度散度、拉格朗日方程、奈奎斯特采样、虚数等抽象难懂数学一网打尽_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1G3411s7bf?p=1首先，这幅图是描述了一个三维的空间：如果不关注Z轴（把Z轴拍扁），就是一个球做圆周运动，

x和y就是就是圆上每个点映射值。这个空间的关键是Z轴，它记录当前小球转了多少圈（度）。

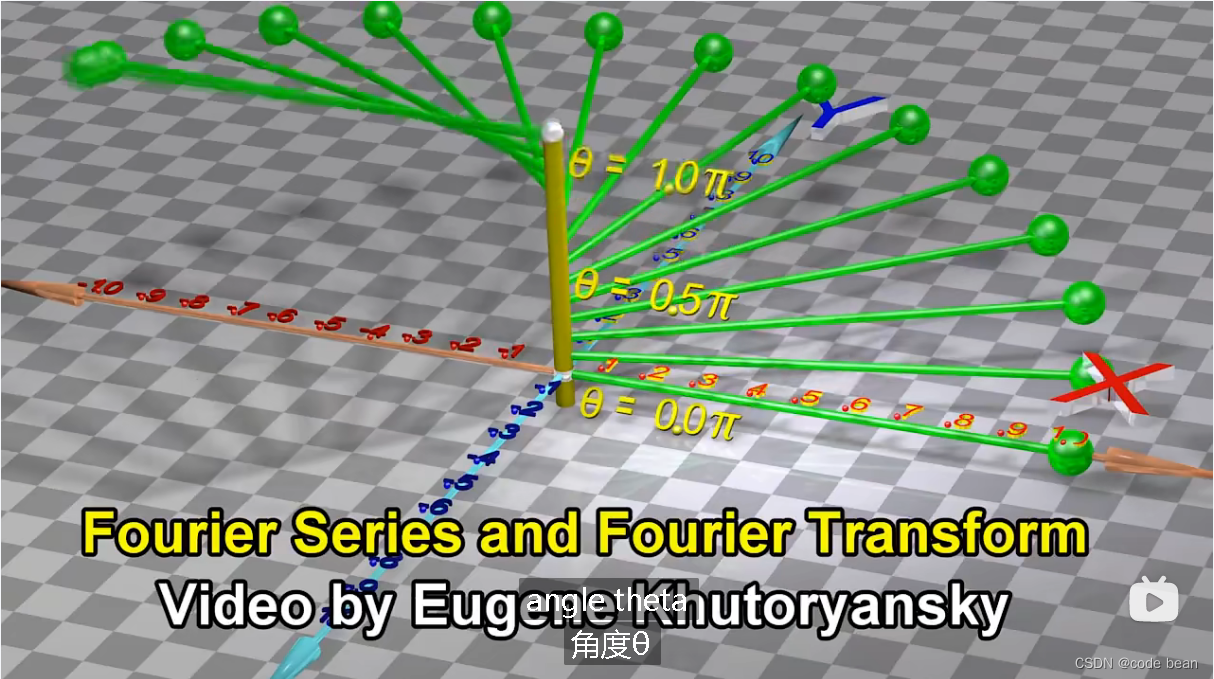
上图中，此时正好转了180°所以此时 =pi

此时，我们回忆一下，三角函数的X轴是啥：

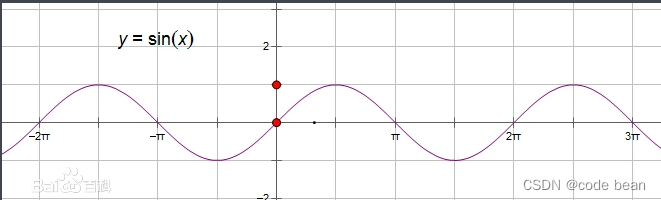
 没错就是图1的Z轴，所以，如果我们将图一换一个方向看：

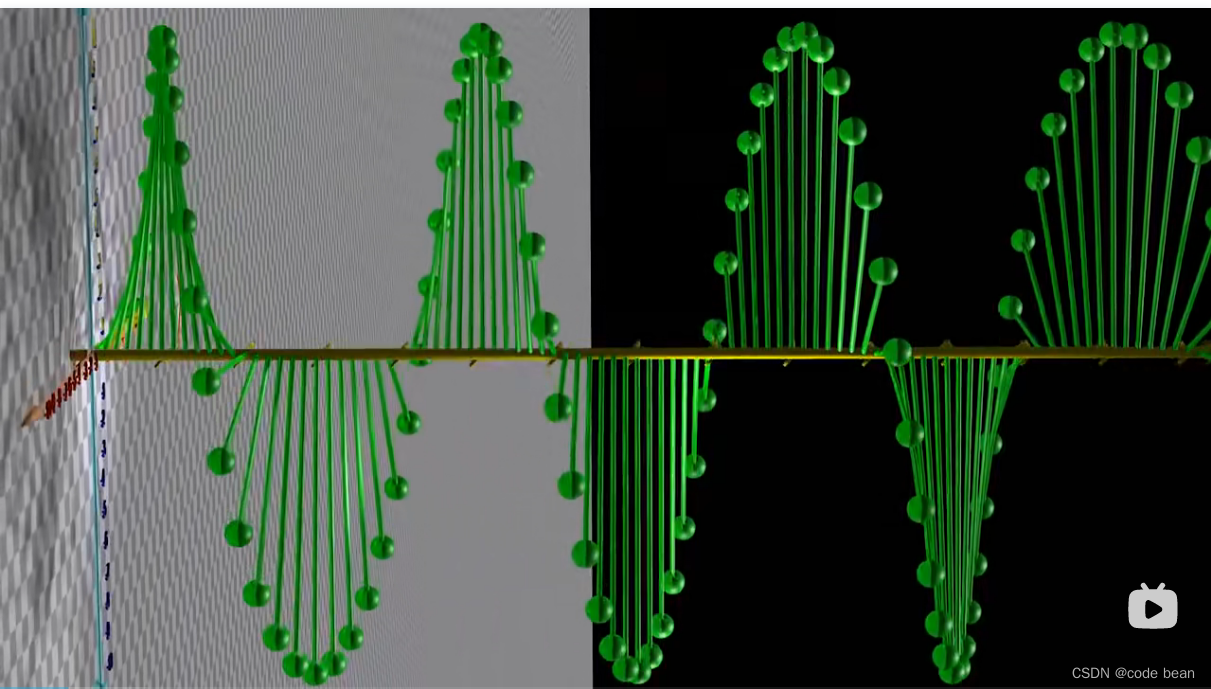
然后将红色X的轴拍扁，只看Y轴和Z轴，我们就得到了一个二维平面图。及Y值随着角度的变换而变换，及正弦函数。

 

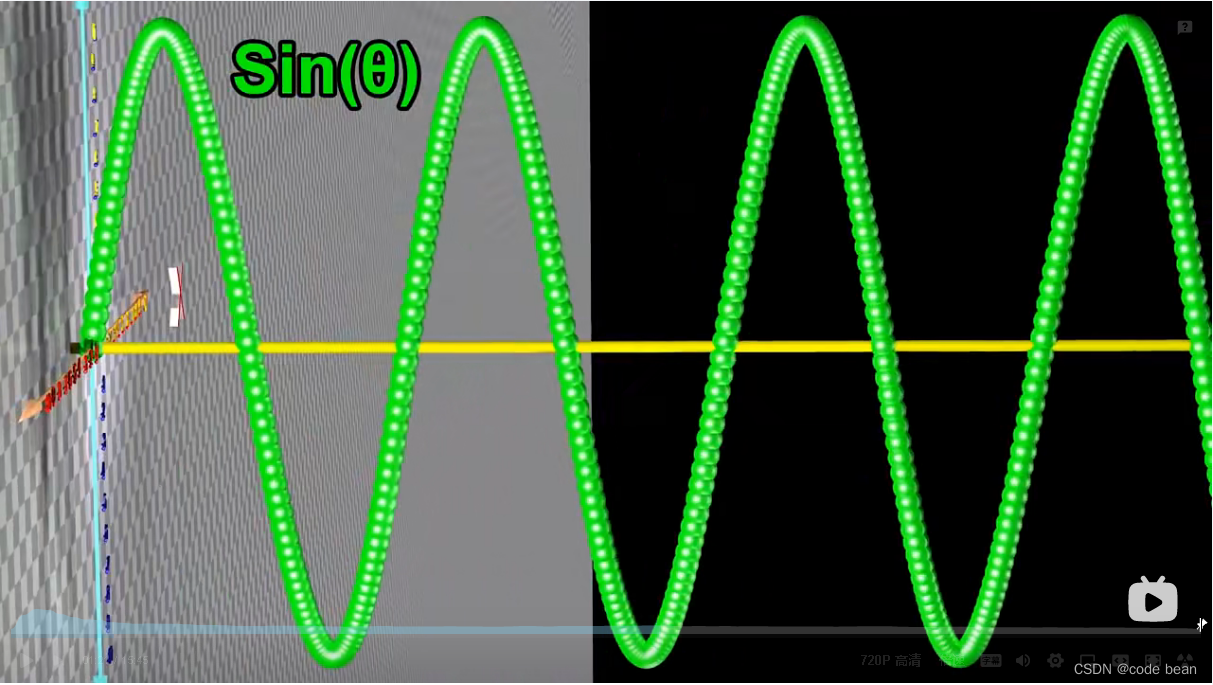
 如果是蓝色轴拍扁，我们将得到是余弦函数，X随着角度的变化

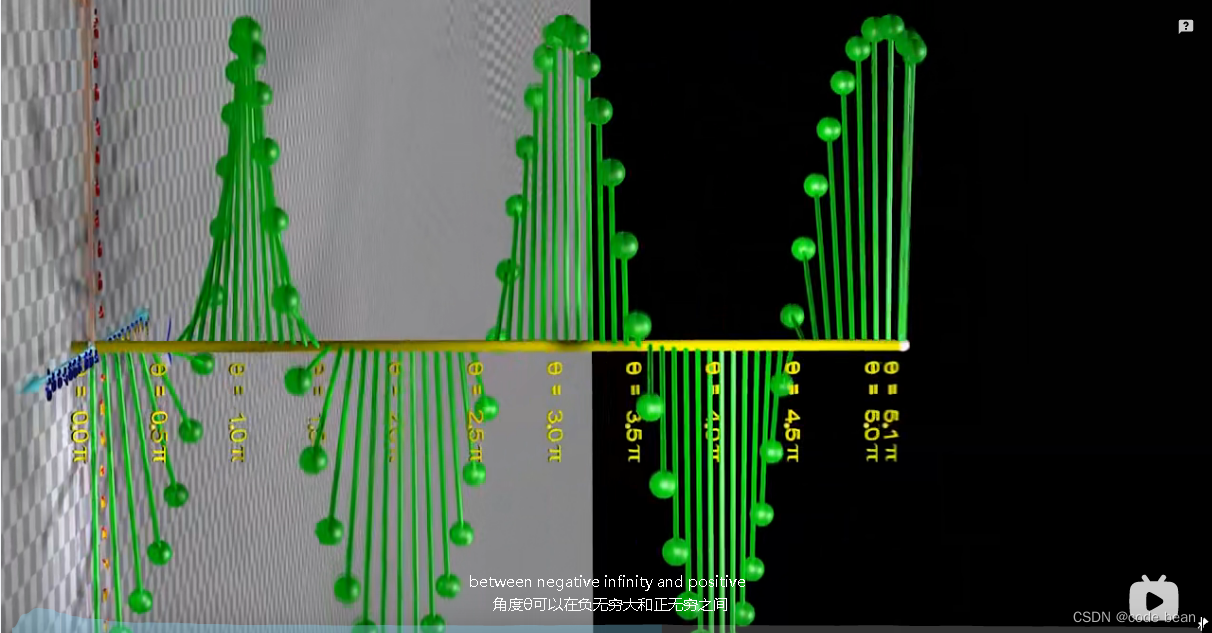
最后，如果是Z轴拍扁，就是个圆周运动了：

如果是两个波形叠加，即两个小球转动，（频率和相位不尽相同）

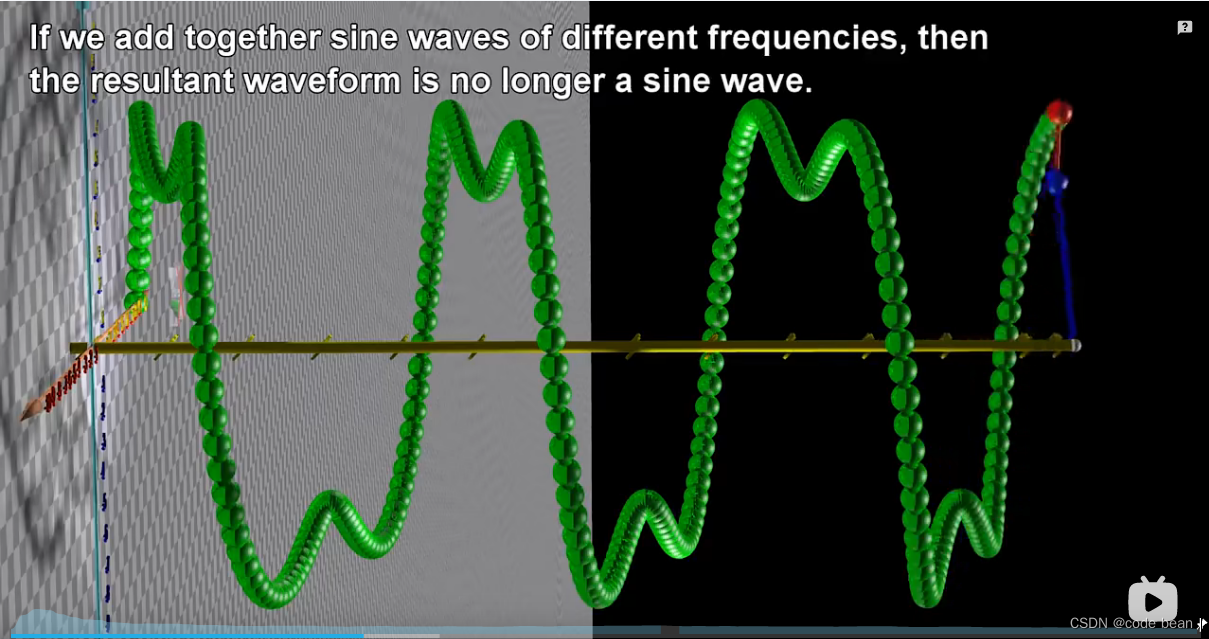
我们将得到一个符合的波形，这就是傅里叶变换的理论基础。 

 

感悟：

在分析问题的时候，有时需要降低维度，使得问题变得更加纯粹，更好分析。

而有的时候，需要升高维度才能解决更复杂的问题：

 

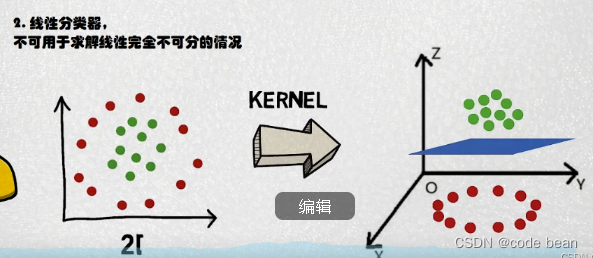
 如上图中，无法通过线性系统将红色球和绿色的球进行分割。

但是如果升高一个维度，就可以轻松的将它们分割。