Bagging和Boosting

集成学习

　　在集成学习中，我们会训练多个模型（通常称为「弱学习器」）解决相同的问题，并将它们结合起来以获得更好的结果。最重要的假设是：当弱模型被正确组合时，我们可以得到更精确和/或更鲁棒的模型。Baggging 和Boosting都属于集成学习的方法，模型融合，将弱分类器融合之后形成一个强分类器，而且融合之后的效果会比最好的弱分类器更好。

bagging

　　Bagging算法（英语：Bootstrap aggregating，引导聚集算法），又称装袋算法。Bagging算法可与其他分类、回归算法结合，提高其准确率、稳定性的同时，通过降低结果的方差，避免过拟合的发生。

基本思想

　　1.给定一个弱学习算法,和一个训练集;

　　2.单个弱学习算法准确率不高;

　　3.将该学习算法使用多次,得出预测函数序列,进行投票;

　　4.最后结果准确率将得到提高.

算法步骤

　　给定一个大小为n的训练集D，Bagging算法从中均匀、有放回地（即使用自助抽样法）选出m个大小为n'的子集Di，作为新的训练集（在训练集中，有些样本可能被多次抽取到，而有些样本可能一次都没有被抽中）。在这m个训练集上使用分类、回归等算法，则可得到m个模型，再通过取平均值、取多数票等方法，即可得到Bagging的结果。

Bagging算法特性

　　1.Bagging通过降低基分类器的方差，改善了泛化误差。

　　2.其性能依赖于基分类器的稳定性；如果基分类器不稳定，bagging有助于降低训练数据的随机波动导致的误差；如果稳定，则集成分类器的误差主要由基分类器的偏倚引起。

　　3.由于每个样本被选中的概率相同，因此bagging并不侧重于训练数据集中的任何特定实例。

boosting

提升方法（Boosting），是一种可以用来减小监督式学习中偏差的机器学习算法。弱学习者一般是指一个分类器，它的结果只比随机分类好一点点；强学习者指分类器的结果非常接近真值。

　　大多数提升算法使用弱学习分类器组成，并将其结果加入一个最终的成强学习分类器。加入的过程中，通常根据它们的分类准确率给予不同的权重。加和弱学习者之后，数据通常会被重新加权，来强化对之前分类错误数据点的分类。Boosting会减小在上一轮训练正确的样本的权重，增大错误样本的权重。（对的残差小，错的残差大）梯度提升的Boosting方式是使用代价函数对上一轮训练出的模型函数f的偏导来拟合残差。

经典Boosting方法

　　Boosting系列算法最经典的包括AdaBoost算法和GBDT算法。

1.AdaBoost算法

　　AdaBoost，是英文"Adaptive Boosting"（自适应增强）的缩写。它的自适应在于：前一个基本分类器分错的样本会得到加强，加权后的全体样本再次被用来训练下一个基本分类器。同时，在每一轮中加入一个新的弱分类器，直到达到某个预定的足够小的错误率或达到预先指定的最大迭代次数。

　　Adaboost 迭代算法步骤：

　　（1）初始化训练数据的权值分布。如果有N个样本，则每一个训练样本最开始时都被赋予相同的权值：1/N。

　　（2）训练弱分类器。具体训练过程中，如果某个样本点已经被准确地分类，那么在构造下一个训练集中，它的权值就被降低；相反，如果某个样本点没有被准确地分类，那么它的权值就得到提高。然后，权值更新过的样本集被用于训练下一个分类器，整个训练过程如此迭代地进行下去。

　　（3）将各个训练得到的弱分类器组合成强分类器。各个弱分类器的训练过程结束后，加大分类误差率小的弱分类器的权重，使其在最终的分类函数中起着较大的决定作用，而降低分类误差率大的弱分类器的权重，使其在最终的分类函数中起着较小的决定作用。换言之，误差率低的弱分类器在最终分类器中占的权重较大，否则较小。

2.GBDT算法

　　GBDT也是集成学习Boosting家族的成员，但是却和传统的Adaboost有很大的不同。回顾下Adaboost，我们是利用前一轮迭代弱学习器的误差率来更新训练集的权重，这样一轮轮的迭代下去。GBDT也是迭代，使用了前向分布算法，但是弱学习器限定了只能使用CART回归树模型，同时迭代思路和Adaboost也有所不同。

　　在GBDT的迭代中，假设我们前一轮迭代得到的强学习器是ft−1(x)ft−1(x), 损失函数是L(y,ft−1(x))L(y,ft−1(x)), 我们本轮迭代的目标是找到一个CART回归树模型的弱学习器ht(x)ht(x)，让本轮的损失函数L(y,ft(x)=L(y,ft−1(x)+ht(x))L(y,ft(x)=L(y,ft−1(x)+ht(x))最小。也就是说，本轮迭代找到决策树，要让样本的损失尽量变得更小。

　　GBDT的思想可以用一个通俗的例子解释，假如有个人30岁，我们首先用20岁去拟合，发现损失有10岁，这时我们用6岁去拟合剩下的损失，发现差距还有4岁，第三轮我们用3岁拟合剩下的差距，差距就只有一岁了。如果我们的迭代轮数还没有完，可以继续迭代下面，每一轮迭代，拟合的岁数误差都会减小。

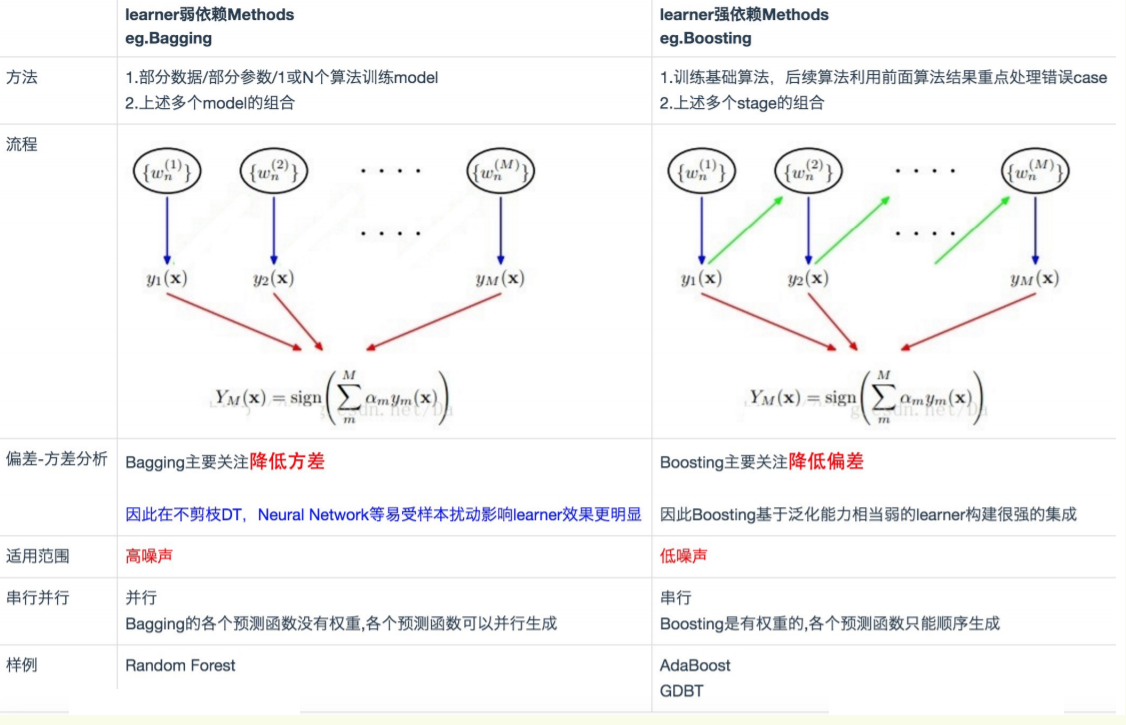
Bagging，Boosting二者之间的区别

1）样本选择：

Bagging：训练集是在原始集中有放回选取的，从原始集中选出的各轮训练集之间是独立的。

Boosting：每一轮的训练集不变，只是训练集中每个样例在分类器中的权重发生变化。而权值是根据上一轮的分类结果进行调整。

2）样例权重：

Bagging：使用均匀取样，每个样例的权重相等

Boosting：根据错误率不断调整样例的权值，错误率越大则权重越大。

3）预测函数：

Bagging：所有预测函数的权重相等。

Boosting：每个弱分类器都有相应的权重，对于分类误差小的分类器会有更大的权重。

4）并行计算：

Bagging：各个预测函数可以并行生成

Boosting：各个预测函数只能顺序生成，因为后一个模型参数需要前一轮模型的结果。

为什么说bagging是减少variance，而boosting是减少bias？

　　Bagging对样本重采样，对每一重采样得到的子样本集训练一个模型，最后取平均。由于子样本集的相似性以及使用的是同种模型，因此各模型有近似相等的bias和variance（事实上，各模型的分布也近似相同，但不独立）。由于 $E[\frac{\sum X_i}{n}]=E[X_i]$ 所以bagging后的bias和单个子模型的接近，一般来说不能显著降低bias。另一方面，若各子模型独立，则有 $Var(\frac{\sum X_i}{n})=\frac{Var(X_i)}{n}$ ，此时可以显著降低variance。若各子模型完全相同，则 $Var(\frac{\sum X_i}{n})=Var(X_i)$ ，此时不会降低variance。bagging方法得到的各子模型是有一定相关性的，属于上面两个极端状况的中间态，因此可以一定程度降低variance。为了进一步降低variance，Random forest通过随机选取变量子集做拟合的方式de-correlated了各子模型（树），使得variance进一步降低。（用公式可以一目了然：设有i.d.的n个随机变量，方差记为 $\sigma^2$ ，两两变量之间的相关性为 $\rho$ ，则 $\frac{\sum X_i}{n}$ 的方差为 $\rho*\sigma^2+(1-\rho)*\sigma^2/n$ ，bagging降低的是第二项，random forest是同时降低两项。详见ESL p588公式15.1）。boosting从优化角度来看，是用forward-stagewise这种贪心法去最小化损失函数 $L(y, \sum_i a_i f_i(x))$ 。例如，常见的AdaBoost即等价于用这种方法最小化exponential loss：。所谓forward-stagewise，就是在迭代的第n步，求解新的子模型f(x)及步长a（或者叫组合系数），来最小化 $L(y,f_{n-1}(x)+af(x))$ ，这里 $f_{n-1}(x)$ 是前n-1步得到的子模型的和。因此boosting是在sequential地最小化损失函数，其bias自然逐步下降。但由于是采取这种sequential、adaptive的策略，各子模型之间是强相关的，于是子模型之和并不能显著降低variance。所以说boosting主要还是靠降低bias来提升预测精度。