浮点编码

存储方式

定点小数存储法

定点小数存储法是一种用于存储小数的方法，它将小数的小数点固定在一个位置上，而不是像浮点数那样使用科学计数法。
在定点小数存储法中，通常会将小数点固定在一个固定的位置（如小数点的右边第n位），并将小数的整数部分和小数部分分别存储在不同的字段
举个例子，如果我们要存储小数 3.14159，可以将小数点固定在第三位，即 314.159，然后将整数部分 314 存储在一个字段中，小数部分 159 存储在另一个字段中。这样就可以用两个整数来表示一个小数。

• 优点：
  精度固定：定点小数存储法的精度是固定的，不会因为小数的大小而改变，这样可以确保计算结果的精度稳定。
  简单性：相比于浮点数存储法，定点小数存储法更简单，实现起来更容易。
• 缺点：
  范围有限：定点小数存储法的范围是有限的，当小数的整数部分或小数部分过大时，可能会导致溢出。
  不适用于极小或极大的数：对于非常接近零或者非常接近最大值的小数，定点小数存储法可能会失去精度，因为小数点的位置固定，无法灵活地表示这些数。

浮点小数存储法

• 符号位（S）：符号位占据一个bit，用于表示浮点数的正负。当符号位为0时，表示正数；当符号位为1时，表示负数。

• 指数位（E）：指数位占据多个bit，通常是8位。指数位用于表示浮点数的指数部分，即小数点的移位数量。指数位的取值范围通常是从0到255，其中特殊值用于表示特殊的情况，例如正无穷大、负无穷大、NaN等。

• 数据位（D）：数据位占据多个bit，通常是23位。数据位用于表示浮点数的有效数字部分，即小数的尾数。数据位存储了小数的二进制表示形式
  S EEEEEEEE DDDDDDDDDDDDDDDDDDDDDDD 一共32位

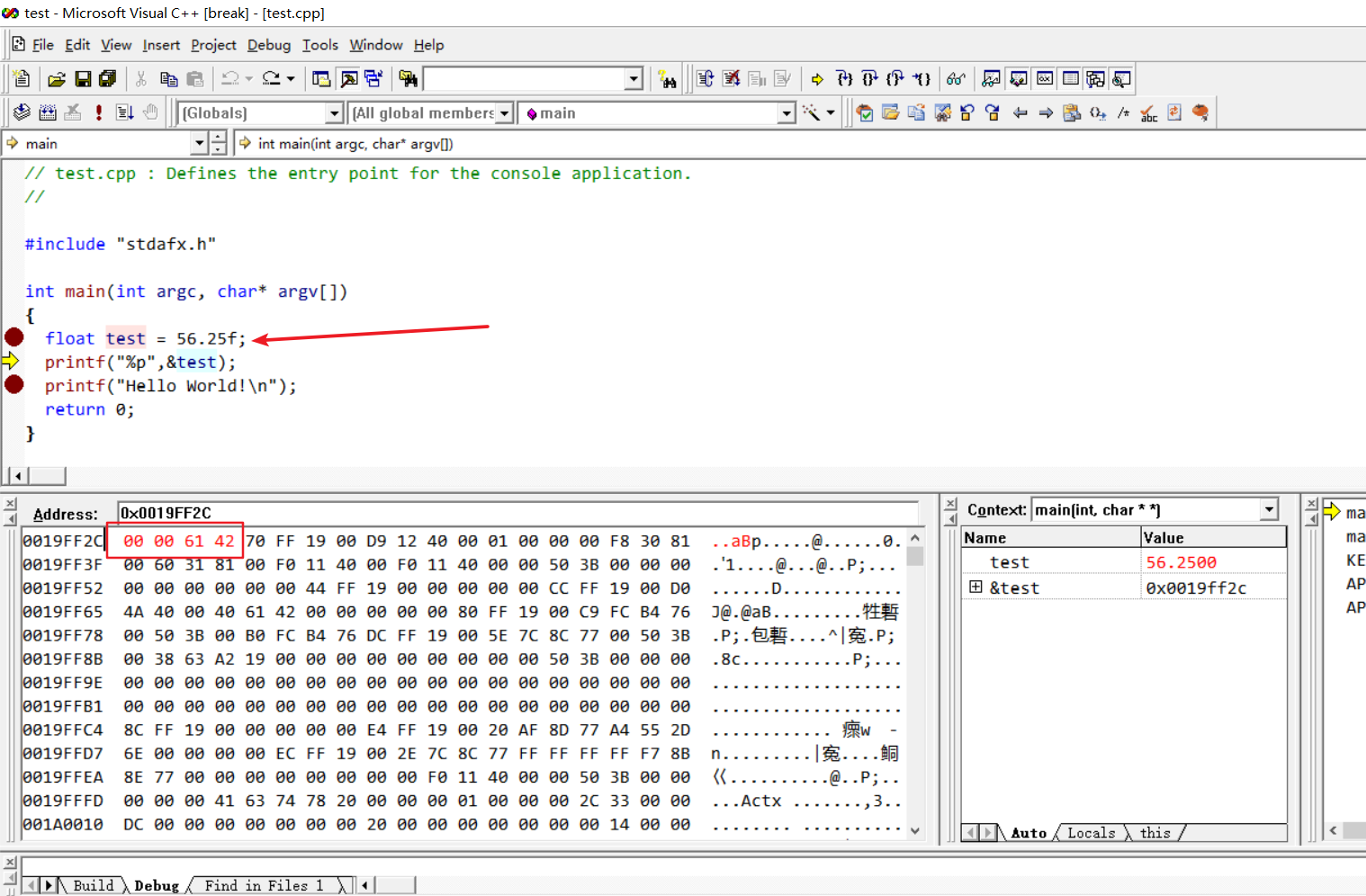
比如56.25是怎么存的首先先将56.25转化位二进制
56转换为二进制为00111000
0.25转换为二进制为0.01
111000.01换为指数表达形式为1.1100001*10^5
S EEEEEEEE DDDDDDDDDDDDDDDDDDDDDDD
0 127+5 1100001
0 128+4 1100001
0 10000100 11000010000000000000000
对上面的二进制四位进行拆分
0100 0010 0110 0001 0000 0000 0000 0000
4 2 6 1 0 0 0 0
小尾方式进行存储
00 00 61 42
验证