逻辑运算（二）

上次我们分别介绍了加法的实现逻辑，这里我们要实现一个减法：

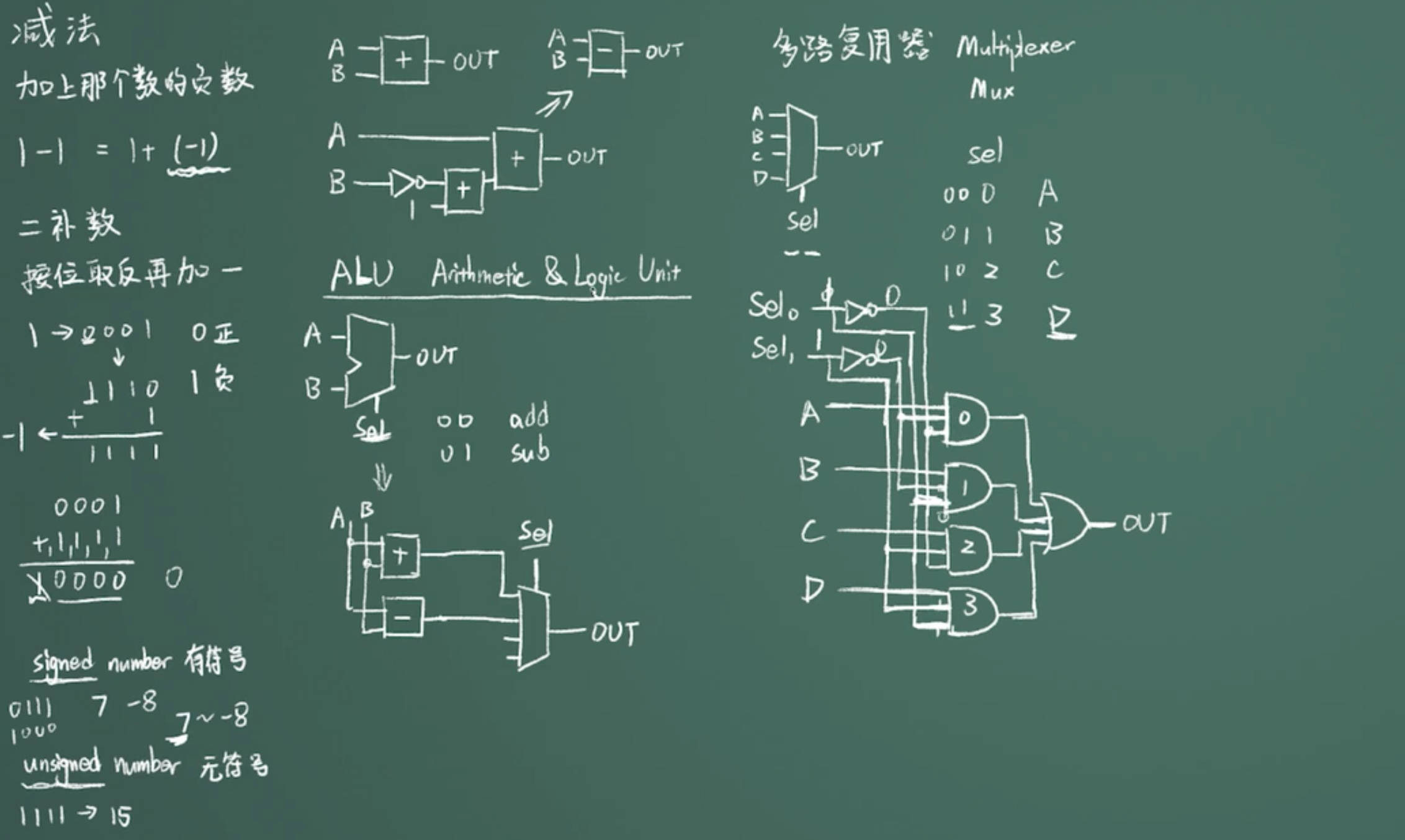
减法的实现：我们知道减去一个数就是加上这个数的负数，如：1-1=1+(-1); 计算机中为了实现这个效果使用了一个新概念：二补数，用来表达一个数的负数。

1、二补数：

    二补数（2's complement）是一种用二进制表示有号数的方法，也是一种将数字的正负号变号的方式，常在计算机科学中使用。在中国大陆称作补码，台湾和香港称为二补数。

　 二补数系统的最大优点是可以在加法或减法处理中，不需因为数字的正负而使用不同的计算方式。只要一种加法电路就可以处理各种有号数加法，而且减法可以用一个数加上另一个数的二补数来表示，因此只要有加法电路及二补数电路即可完成各种有号数加法及减法，在电路设计上相当方便。另外，二补数系统的 0 只有一个表示方式，这点和一补数系统不同（在一补数系统中，0 有二种表示方式），因此在判断数字是否为 0 时，只要比较一次即可。右侧的表是一些 8-bit 二补数系统的整数。它的可表示的范围包括-128到127，总共256 (2⁸)个整数。

 

2、数字表示方式：更多资料：https://www.cnblogs.com/milantgh/p/3925425.html

　　以下用 4 比特的二补数数字来说明二补数系统的数字表示方式。

• 在表示正数和零时，二补数数字和一般二进制一样，唯一的不同是在二补数系统中，正数的最高比特恒为 0，因此4 比特的二补数正数，最大数字为 0111 (7)。
• 二补数数字的负数，最高比特恒为 1，4 比特二补数的数字中，最接近 0 的负数为 1111 (-1)，以此类推，因此绝对值最大的负数是 1000 (-8)。

　　以上的表示方式在电脑处理时格外方便，用以下的例子说明：

　　0011  (3)
  + 1111 (-1)
 --------------
   10010  (2)

3、二补数计算方式

　　在计算二进制数字的二补数时，会将数字进行比特反相运算，再将结果加 1，不考虑溢出比特（一般情形，溢出比特会为 0），就可以得到该数字的二补数。

　　以下考虑用有号数 8 比特二进制表示的数字 5：

0000 0101 (5)

　　其最高比特为 0，因为此数字为正数。若要用二补数系统表示 -5，首先要将 5 的二进制进行反相运算〔1 变为 0，0 变为 1 〕：

1111 1010

　　目前的数字是数字 5 的一补数，因此需要再加 1，才是二补数：

1111 1011 (-5)

　　以上就是在二补数系统中 -5 的表示方式。其其最高比特为 1，因为此数字确实为负数。

　　一个负数的二补数就是其对应的正数。以 -5 为例，先求数字的一补数：

0000 0100

　　再加一就是 -5 的二补数，也就是 5。

0000 0101 (5)

　　简单来说，数字 a (正负数皆可)的二补数即为 -a。

 

Logisim实现减法

 

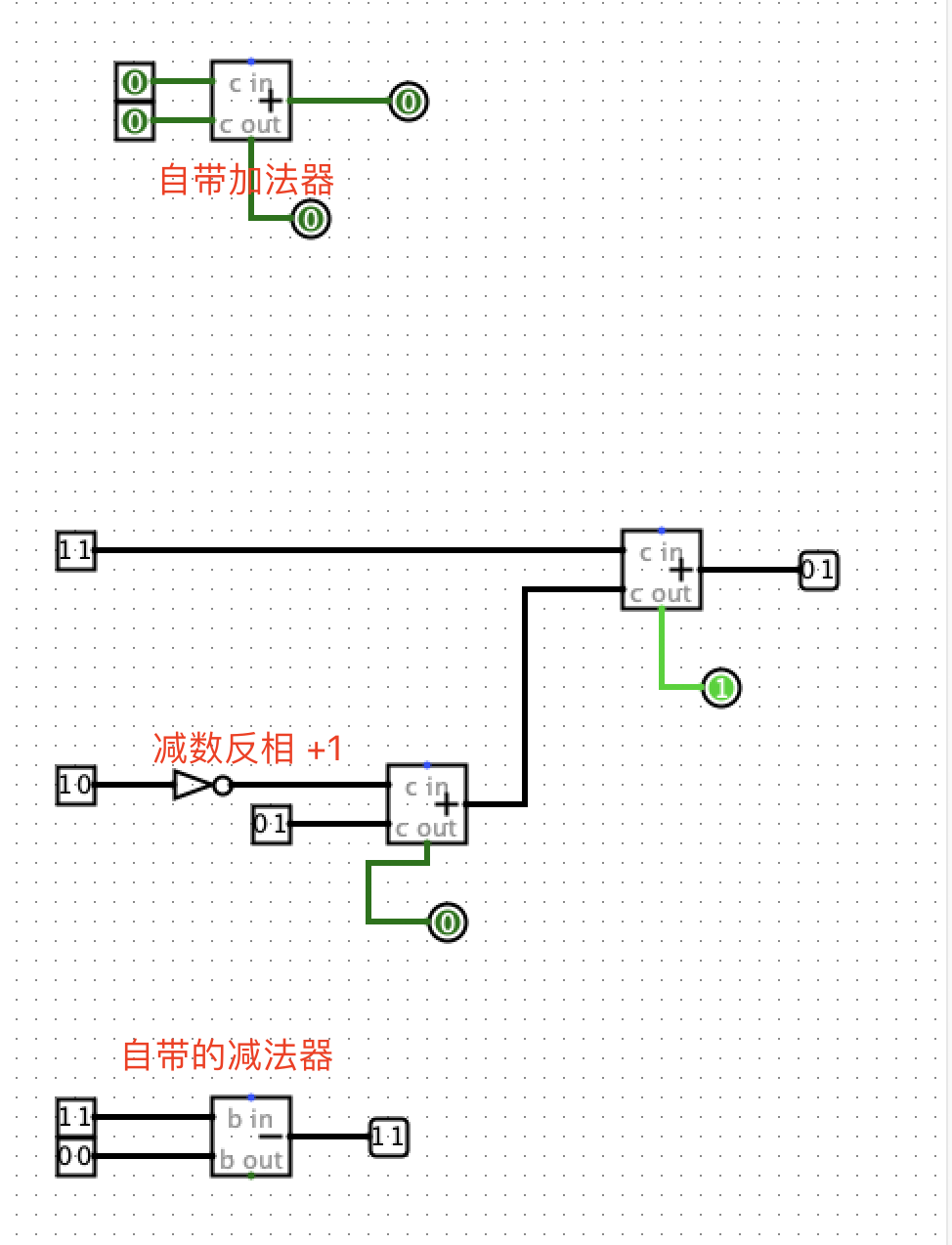
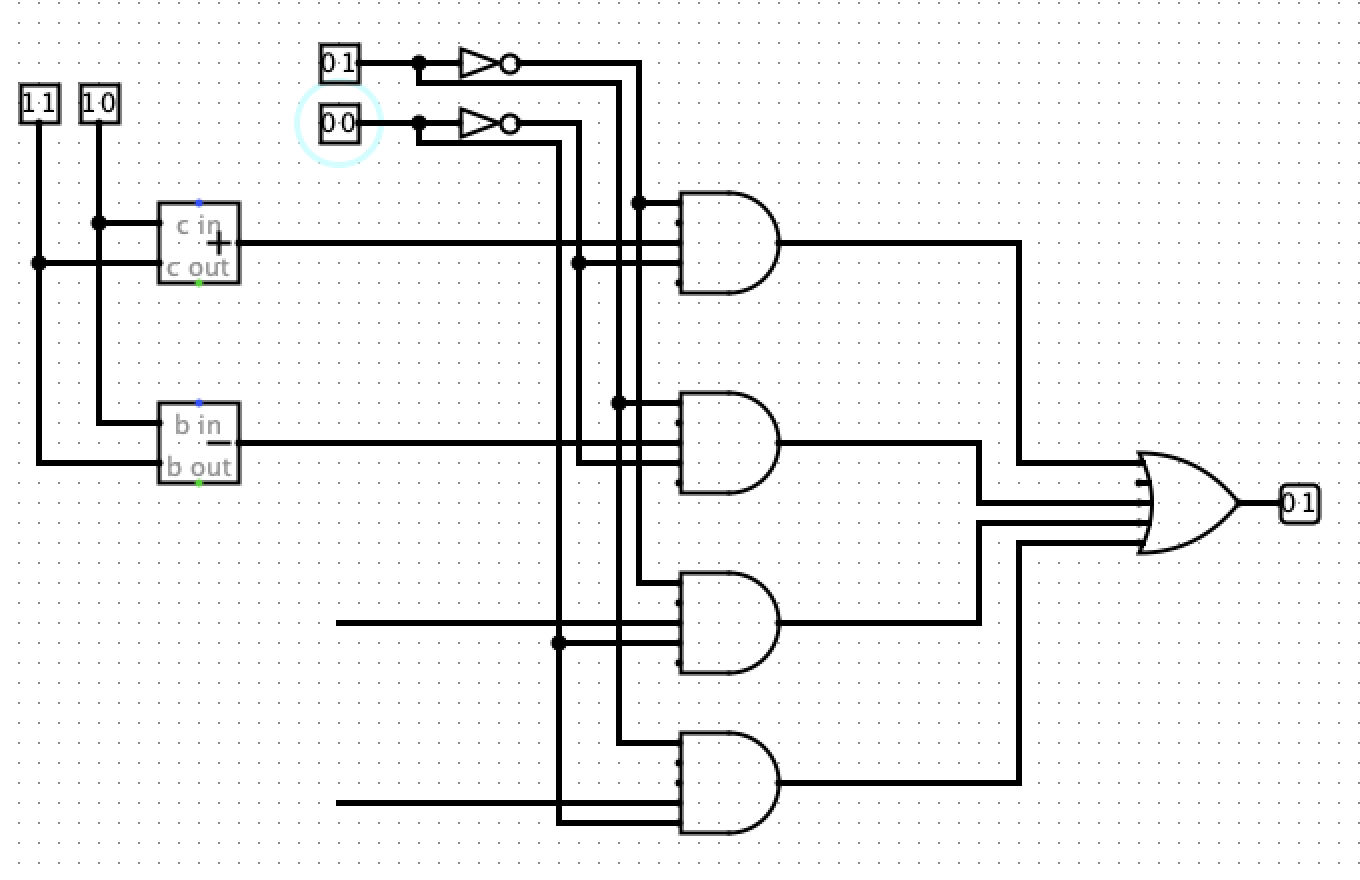
运算单元ALU（Arithmetic & Logic Unit）

 

主要作用是通过选择，是传入ALU中的数据进行怎样的运算，是减法？还是加法等。

 

最后总结下：