浅析快速傅里叶变换(FFT)
写在前面:作者学这个算法时才小升初,如果文章讲的有问题请轻喷。
哈喽大家好,我是 doooge,今天给大家来点想看的东西啊。
1. 前置知识
工欲善其事,必先利其器,讲 FFT 之前我先将一些废话,如果你是 dalao 你也可以不听。
1.1 复数
高中数学里的一个非常高深的东西叫做虚数,但是它的定义很简单:
而复数,就是虚数和实数相结合的东西, 它的表现方式为 \(a+bi\),这个东西的运算比较简单,我在这里稍稍赘述一下:
至于除法嘛,就不太需要了,绝对不是因为我懒(
那我们怎么才能表示一个复数呢?我们可以用两个轴,实数轴和虚数轴,这个玩意叫复平面:
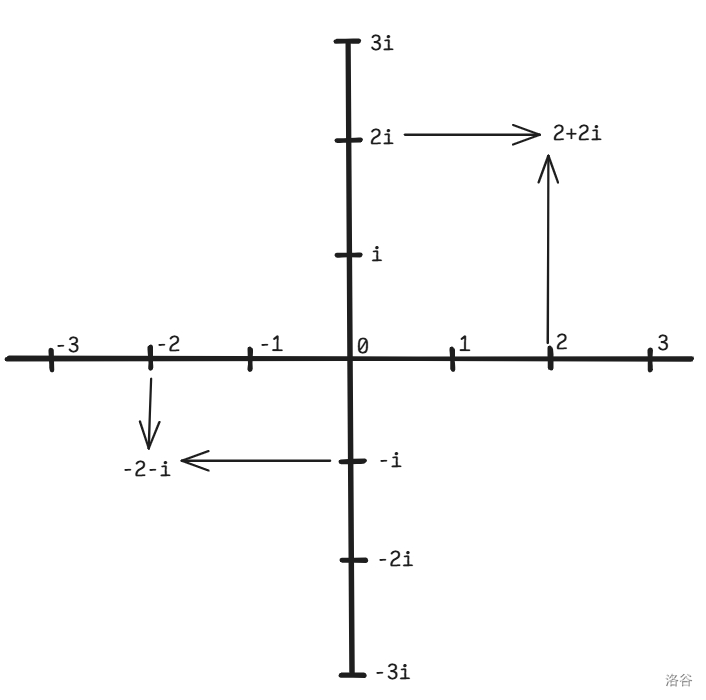
在 c++ 中,STL 提供了 complex 类型来表示复数,但是我个人更倾向于用结构体来定义:
struct Mycomplex{
double x,i;
Mycomplex operator+(const Mycomplex &a){return {x+a.x,i+a.i};}
Mycomplex operator-(const Mycomplex &a){return {x-a.x,i-a.i};}
Mycomplex operator*(const Mycomplex &a){return {x*a.x-i*a.i,x*a.i+i*a.x};}
}a[1000010];
1.2 单位根
我们在复平面上画一个半径为 \(1\) 的圆,圆的边上每一个点都满足 \(x^2+y^2=1\),也就是每一个点都满足它到 \((0,0)\) 的点的距离为 \(1\)。
了解 FFT 前,我们先要知道 \(n\) 次单位根,定义 \(\omega_{n}\) 为 \(x^n=1\) 的根,如果 \(x\) 只能为实数,显然最多只能有两个根 \(1\) 和 \(-1\),但是我们转到复数上时,这样的根有 \(n\) 个:\(\omega_n^0,\omega_n^1,\cdots,\omega_n^{n-1}\)。
也就是:
我们把它放在图上,不难看出 \(-\omega_n^x=\omega_n^{\frac{n}{2}+x}\):
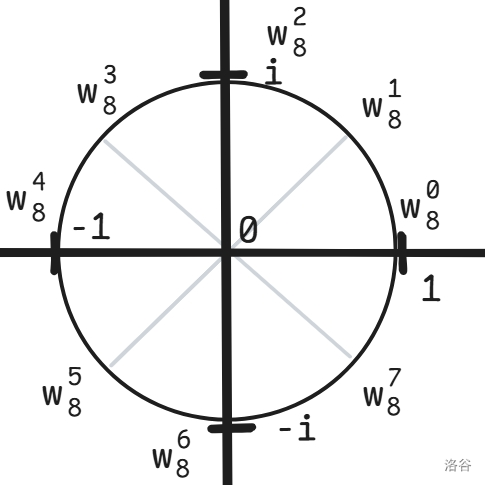
但是如果这样就下结论的话,也太扯淡了,我们还需要证明,证明如下:
- 当 \(x=1\),显然成立。
- 当 \(x=k-1\) 成立时,\(w_{n}^k=w_{n}^{k-1}\cdot w_{n}^1=(\cos (k-1)+i\sin(k-1))\cdot (\cos 1+i \sin 1)=\cos k+i\sin k\)。
证毕。
1.3 多项式
设有一个 \(n\) 次多项式 \(f(x)\),我们有 \(n\) 个系数 \(a_0,a_1,\cdots,a_{n-1}\):
显然可以用 \(n\) 个系数来表示这个多项式,这个东西叫做系数表示法。
我们可以用 \(n\) 个点 \((x_0,y_0),\cdots,(x_{n-1},y_{n-1})\) 来表示一个 \(n-1\) 次的多项式(至于为什么我也不知道),这个东西叫做点值表示法,感兴趣的可以自己去搜一下。
1.4 多项式乘法
记乘出的多项式用系数表示法为 \(C\),乘起来的两个多项式为 \(A\) 和 \(B\),那么:
如果是用点值表示法那就更简单了:
是不是挺像高精度的?
好了,前置知识就这么多了,正片开始!
2. 快速傅里叶变换(FFT)
我们先从一道例题开始
有两个多项式 \(A\),\(B\),它们的次数分别为 \(n\) 和 \(m\),求出它们的乘积。
\(n,m\le10^5\)。
如果用暴力乘起来,复杂度 \(O(n^2)\),不够优秀,考虑将系数转换成点值。
如果我们直接暴力枚举 \(n+1\) 个点表示系数,在将系数相乘,复杂度 \(O(n^2)\),不够优秀。我们尝试换一种方法。
假设原本的多项式为 \(A\),我们重新设两个多项式 \(A_0\) 和 \(x\) 倍 \(A_1\) 来表示 \(A\) 中的第偶数、奇数项函数,就比如:
不难看出:
但是,\(x^2\) 是个正数,没办法变负,所以我们可以用我们上面说过的 \(w_{n}^{x}\) 来处理 \(A_0\) 和 \(A_1\):
我们可以递归求解 \(A_0\) 和 \(A_1\)。具体来说,我们已经求出了 \(A_0,A_1\) 在 \(x\) 等于 \(\omega_{n}^{0},\omega_{n}^{1},\cdots,\omega_{n}^{n-1}\) 时的值,我们就能在 \(O(n)\) 的情况下求出 \(A\) 在这些地方的值。
代码:
const double pi=3.141592653589793238;//这个不用背多长,12位左右就行
//也可以这样写#define pi acos(1.0),但是精度可能不够
void FastFastTLE(Mycomplex a[],int n){
if(n==1){
return;
//系数为1时,怎么递归都一样了,这里直接返回
}
Mycomplex a0[(n>>1)+1],a1[(n>>1)+1];//保证每层空间都是线性,但是别忘了+1
for(int i=0;i<n;i++){
if(i&1)a1[i>>1]=a[i];
else a0[i>>1]=a[i];
}//处理系数
FastFastTLE(a0,n>>1),FastFastTLE(a1,n>>1);
Mycomplex w_n1={cos(2*pi/n),sin(2*pi/n)},W={1,0};//W初始为w_n^0
for(int i=0;i<n>>1;i++){
a[i]=a0[i]+W*a1[i];
a[i+(n>>1)]=a0[i]-W*a1[i];
W=W*w_n1;//w_ni=w_n(i-1)*w_n^1
}
return;
}
3. FFT 逆变换(IFFT)
我们现在虽然能够将一个多项式转化成点值表示法,但是我们因该如何将他转回系数表示法呢?回想一下,为什么我们要给 \(A\) 找 \(\omega_{n}^x\) 这样的取值,当然是因为它的特殊性质。
这里给一个结论:我们知道了 \(A\) 的 \(\omega_n^i\),我们设 \(B\) 的系数 \(B_i=A\) 的 \(w_n^i\) 处的取值,取单位根的共轭 \(\omega_n^0,\omega_n^{-1},\cdots,\omega_n^{-(n-1)}\),再带入 \(B\),得出结果 \(C\) 的各项除上 \(n\),就是 \(A\) 的各个系数。
下面给出证明:
首先设多项式 \(A\):
再设 \(y_0,y_1,\cdots,y_{n-1}\) 为 \(A\) 的傅里叶变换,设多项式 \(B\):
将 \(\omega_n^0,\omega_n^{-1},\cdots,\omega_n^{-(n-1)}\) 代入 \(B\),得到 \((z_0,z_1,\cdots,z_n)\),而此时:
当 \(j-k=0\) 时,\(\sum_{i=0}^{n-1}(\omega_{n}^i)^{j-k}=n\),否则,我们可以用等比数列求和公式 \(S_n=\frac{a_1(1-q^n)}{1-q}\) 得到:
所以 \(z_k=n\cdot a_k\),\(a_k=\frac{z_k}{n}\),证毕。
我们就能愉快的 FFT 了!但是先别急,虽然递归 FFT 的时间 / 空间复杂度都是 \(O(n\log n)\),但是常数比较大,我们还要进一步优化。
4. 非递归版 FFT
我们尝试优化 FFT 的递归过程。
我们知道递归 FFT 是让这个多项式的奇偶分开再分别递归,我们能否找到一些规律呢?当然可以,画个图试试,假设 \(n=8\):
\(0,1,2,3,4,5,6,7\)
\(0,2,4,6|1,3,5,7\)
\(0,4|2,6|1,5|3,7\)
结果:
\(0,4,2,6,1,3,5,7\)
看不出什么规律?我们把这个数列初始和结束的二进制写出来:
\((000)_2,(001)_2,(010)_2,(011)_2,(100)_2,(101)_2,(110)_2,(111)_2\)
\((000)_2,(100)_2,(010)_2,(110)_2,(001)_2,(101)_2,(011)_2,(111)_2\)
注意:n 必须要是 2 的次幂,我们可以在前面补 0 解决。
欸?开始和结束每个数字的二进制区别不就是翻转了一遍吗?
处理起来是这样的:
rev[0]=0;//rev[i]表示i二进制转换后的值
for(int i=1;i<n;i++){
rev[i]=(rev[i>>1]>>1)|((i&1)*(1<<(l>>1)));//前i-1位转换后的值+这一位要不要翻转
}
然后呢?我们可以模拟它合并的过程,下面给出代码:
void FastFastTLE(Mycomplex A[],int n,int typ){//typ=1为正变换,typ=-1为逆变换
for(int i=0;i<n;i++){//处理交换
if(i<rev[i])swap(A[i],A[rev[i]]);
}
for(int l=1;l<n;l<<=1){//枚举长度
Mycomplex w={cos(pi/l),typ*sin(pi/l)};
for(int i=0;i<n;i+=l<<1){//枚举每一次合并的位置
Mycomplex o={1,0};
for(int j=0;j<l;j++){
Mycomplex x=A[i+j],y=A[i+j+l]*o;
A[i+j]=x+y;
A[i+j+l]=x-y;
o=o*w;
}
}
}
return;
}
5. 完整代码
模板题:P3803 【模板】多项式乘法(FFT),P1919 【模板】高精度乘法 | A*B Problem 升级版。
#include<bits/stdc++.h>
using namespace std;
const double pi=3.141592653589793238;
struct Mycomplex{
double x,i;
Mycomplex operator+(const Mycomplex &a){return {x+a.x,i+a.i};}
Mycomplex operator-(const Mycomplex &a){return {x-a.x,i-a.i};}
Mycomplex operator*(const Mycomplex &a){return {x*a.x-i*a.i,x*a.i+i*a.x};}
}a[3000010],b[3000010],c[30000010];//建议开3倍空间防止RE
int rev[3000010],n=1;
void init(){//预处理翻转和w_n^i
rev[0]=0;
for(int i=1;i<n;i++){
rev[i]=(rev[i>>1]>>1)|((i&1)*(n>>1));
}
return;
}
void FastFastTLE(Mycomplex A[],int n,int typ){//typ=1为正变换,typ=-1为逆变换
for(int i=0;i<n;i++){//处理交换
if(i<rev[i])swap(A[i],A[rev[i]]);
}
for(int l=1;l<n;l<<=1){//枚举长度
Mycomplex w={cos(pi/l),typ*sin(pi/l)};
for(int i=0;i<n;i+=l<<1){//枚举每一次合并的位置
Mycomplex o={1,0};
for(int j=0;j<l;j++){
Mycomplex x=A[i+j],y=A[i+j+l]*o;
A[i+j]=x+y;
A[i+j+l]=x-y;
o=o*w;
}
}
}
return;
}
int main(){
int N,M;
cin>>N>>M;
for(int i=0;i<=N;i++){
cin>>a[i].x;
}
for(int i=0;i<=M;i++){
cin>>b[i].x;
}
while(n<=N+M)n<<=1;
//特别注意这里n必须要是2的整数次幂!!!
init();
FastFastTLE(a,n,1);
FastFastTLE(b,n,1);
for(int i=0;i<=n;i++){//直接乘点值
c[i]=a[i]*b[i];
}
FastFastTLE(c,n,-1);
for(int i=0;i<=N+M;i++){
printf("%d ",int(c[i].x/n+0.5));//注意这里的四舍五入
}
cout<<endl;
return 0;
}//完结撒花!!!
模版 2,我们可以将多项式中的 \(x\) 代入成 \(10\),最后再处理一下进位就行了:
#include<bits/stdc++.h>
using namespace std;
const double pi=3.141592653589793238;
struct Mycomplex{
double x,i;
Mycomplex operator+(const Mycomplex &a){return {x+a.x,i+a.i};}
Mycomplex operator-(const Mycomplex &a){return {x-a.x,i-a.i};}
Mycomplex operator*(const Mycomplex &a){return {x*a.x-i*a.i,x*a.i+i*a.x};}
}a[3000010],b[3000010],c[30000010];//建议开3倍空间防止RE
int rev[3000010],n=1;
void init(){//预处理翻转和w_n^i
rev[0]=0;
for(int i=1;i<n;i++){
rev[i]=(rev[i>>1]>>1)|((i&1)*(n>>1));
}
return;
}
void FastFastTLE(Mycomplex A[],int n,int typ){//typ=1为正变换,typ=-1为逆变换
for(int i=0;i<n;i++){//处理交换
if(i<rev[i])swap(A[i],A[rev[i]]);
}
for(int l=1;l<n;l<<=1){//枚举长度
Mycomplex w={cos(pi/l),typ*sin(pi/l)};
for(int i=0;i<n;i+=l<<1){//枚举每一次合并的位置
Mycomplex o={1,0};
for(int j=0;j<l;j++){
Mycomplex x=A[i+j],y=A[i+j+l]*o;
A[i+j]=x+y;
A[i+j+l]=x-y;
o=o*w;
}
}
}
return;
}
int main(){
string s,s2;
cin>>s>>s2;
int N=s.size(),M=s2.size();
for(int i=N-1;i>=0;i--)a[N-1-i].x=s[i]-'0';
for(int i=M-1;i>=0;i--)b[M-1-i].x=s2[i]-'0';
while(n<=N+M)n<<=1;
//特别注意这里n必须要是2的整数次幂!!!
init();
FastFastTLE(a,n,1);
FastFastTLE(b,n,1);
for(int i=0;i<=n;i++){//直接乘点值
c[i]=a[i]*b[i];
}
FastFastTLE(c,n,-1);
for(int i=0;i<=n;i++){
c[i].x/=n;
}
for(int i=0;i<=n;i++){
c[i+1].x+=int(c[i].x+0.5)/10;
}
while(int(c[n].x+0.5)==0)n--;
for(int i=n;i>=0;i--){
printf("%d",int(c[i].x+0.5)%10);//注意这里的四舍五入
}
cout<<endl;
return 0;
}//完结撒花!!!
6. FFT 优化:三步变两步
在上文中的 FFT 做法是先将 \(A\),\(B\) 变换,再将点值相乘,得到的点值变换回来得到的。
但是,我们可以用另一种方法:将多项式 \(B\) 的实数项复制到 \(A\) 的复数项,也就是:
将 \(A\) 变换成点值,再平方一下,也就是乘自己。这时,将 \(A\) 转换回来。
我们知道 \((A+B_i)^2=A^2-B^2+i\cdot 2AB\),于是我们可以将转换回来的结果开一下平方,这时,答案就在结果复数项里面了!
这个方法可以优化部分常数,但是一般用不到(除非卡常),并且我不想写。
7. 闲话
膜拜巨佬 _FastFT2013 教会了我 FFT 并订正了文章中的错误,感激不尽,顺便推一下他和另一位同机房大佬 @Sunrise_beforeglow 的文章,写的很好。
蒟蒻不才,膜拜大佬,如果文章有什么错字等问题,请在评论区提醒我。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号