浅析扫描线
哈喽大家好,我是 doooge,今天来点大家想看的东西啊。
前置知识
线段树,离散化,没了
1. 扫描线矩形面积并
有 \(n\) 个矩形,每个矩形的下表为 \(x_i\),\(y_i\),\(x2_i\),\(y2_i\),求这些矩形的面积并。
\(n\le10^4\),\(x_i,x2_i,y_i,y2_i\le 10^9\)。
暴力做法就不多说了,我们直接来讲扫描线
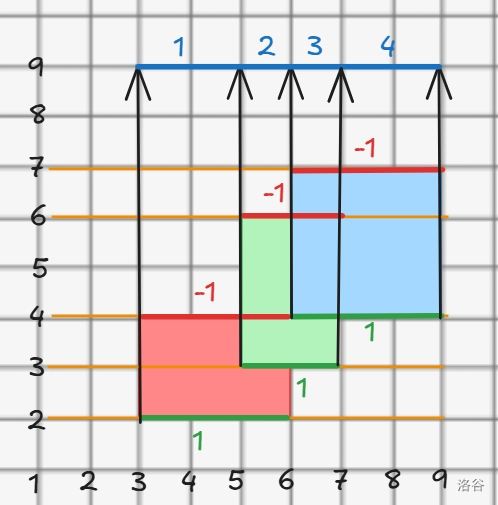
我们先拿个例子(横轴为 \(y\),纵轴为 \(x\))
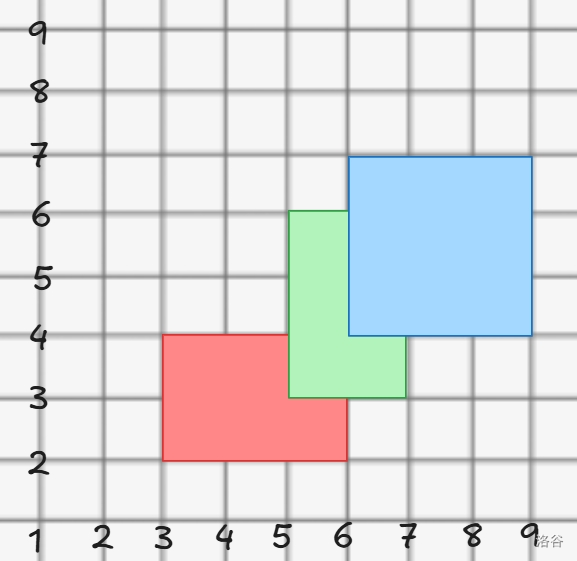
扫描线的步骤是按照横轴 / 纵轴上的边,把这个图片分割成几个矩形:
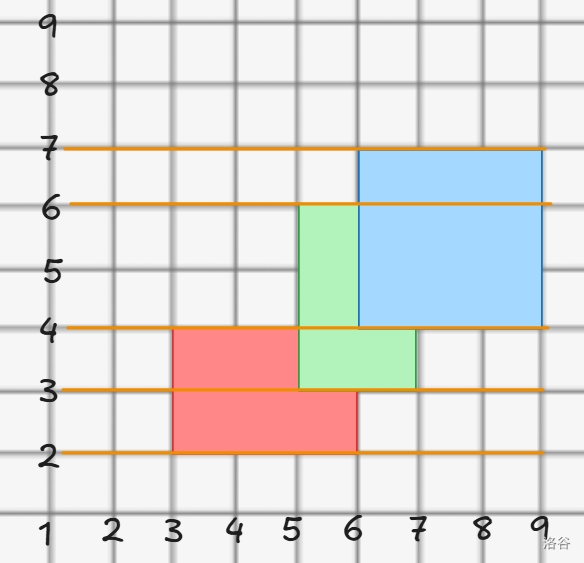
我们从下往上开始扫,每次碰到横边就停下来,与上一次找到的横边连成一个矩形,就像这样:
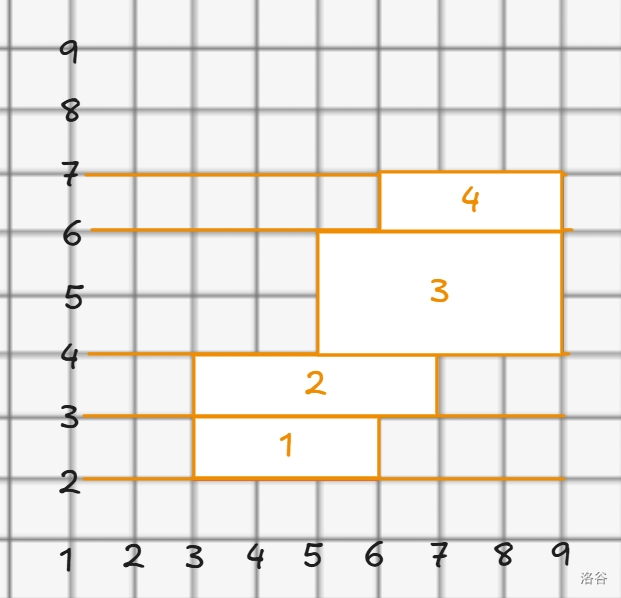
显然,我们计算的答案只与横边的在 \(y\) 轴的坐标有关
那我们需要怎样才能知道哪些地方有面积,哪些地方是空的呢?
我们需要分别讨论对于每个矩形的下边和上边,我们可以给这些矩形的横边赋个边权,具体来说,我们给下边赋上 \(-1\),上边赋上 \(1\) 来区分:
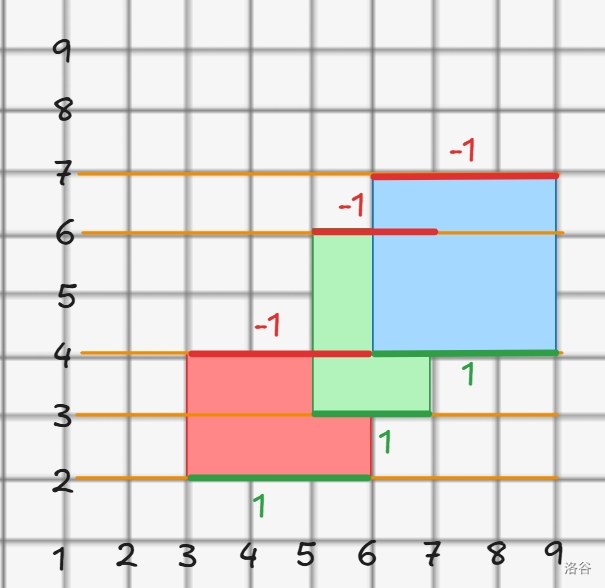
我们首先给横边按 \(x\) 来排序,这样能保证在遍历过程中的权值和一定 \(>0\),扫描线所截的长度一定不是非负的了。
但是,如果有两条线段相交,中间的地方重合了,此时相交的部分我们只能算一遍,那我们该怎么办呢?
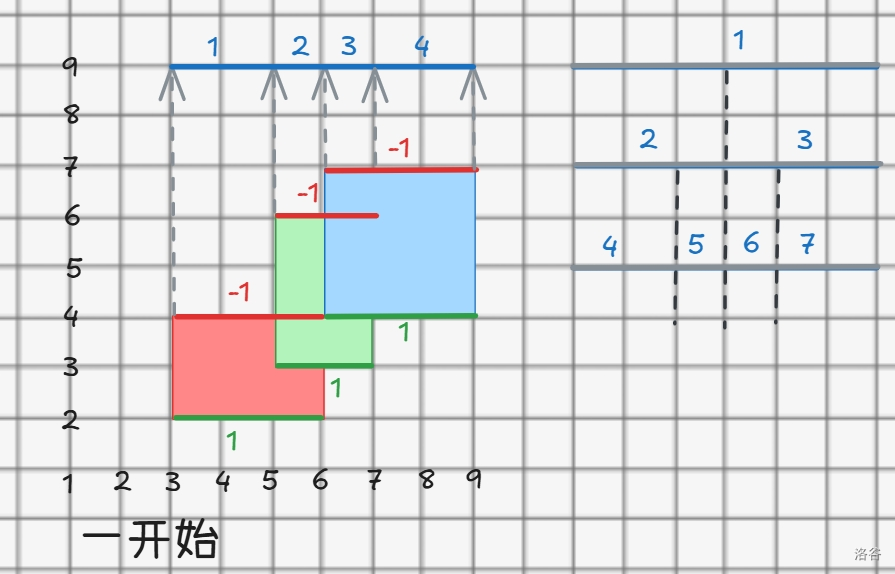
于是,离散化出场了!
我们把 \(y\) 轴离散化,把它们都丢尽一个数组里面,在进行去重,于是离散化完了这些点后,我们就可以将相邻的一条点建边就行了
因为我们建出来的新线段都是连续的,所以可以用线段树来维护这些小区间
那我们线段树该维护什么呢?这个其实不难:
- 这个区间的左,右坐标
- 这个区间实际上覆盖了的长度
- 这个区间被多少个矩形包含
于是这道题就变成了一道维护区间的题目,有扫描线扫到的线数次修改,每次修改一个区间(矩形上面的一条横边)\(+1\) 或者 \(-1\),要你计算此时扫描线包含的线段长度 \(\times\) 这条线与下一条线相差的高度
我们来试着模拟一下:
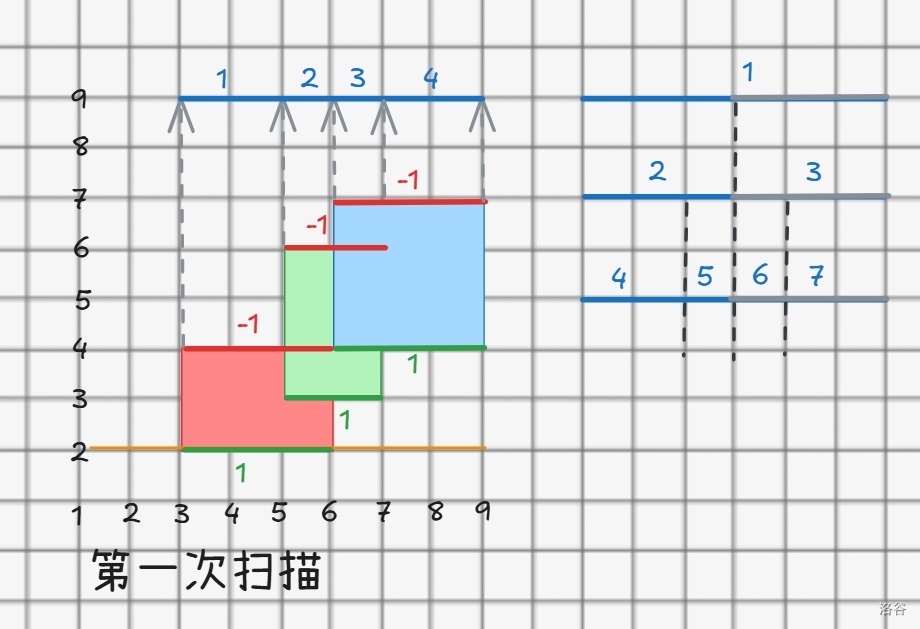
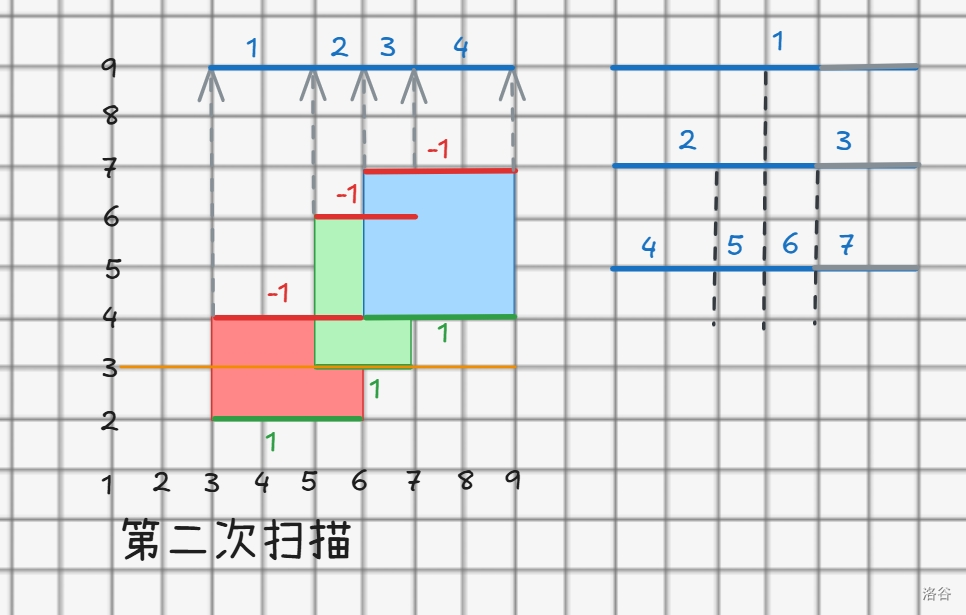

2. 扫描线矩形面积并的代码
2.1 线段树部分
模板题:P5490
先从定义节点开始,这个前面说过了,值得一提的是,因为只有点数 \(-1\) 条边,所以 \(l\) 到 \(r\) 表示的是 \(a_l\) 到 \(a_{r+1}\) 的区间:
struct Node{//线段树节点
int l,r,sum,cnt;
//l和r表示t[i]维护a[l]到a[r+1](注意,是+1!看了完整代码你就知道为什么了)的区间
//sum表示目前这个区间包含的线段的长度
//cnt表示目前有多少个矩形完全包含这个线段
}t[8000010];//2n个点再加上四倍空间就是8倍空间
pushup 也不难写,注意这个判断覆盖可写可不写,具体要看你的 update 咋写的:
void pushup(int x){
if(t[x].cnt){//这个线段被覆盖过
t[x].sum=a[t[x].r+1]-a[t[x].l];//因为a[r+1]-a[l]的长度才是a[l]到a[r]的长度
}else{
t[x].sum=t[ls(x)].sum+t[rs(x)].sum;
}
return;
}
update 跟正常的 update 差不多,但是如果你是用判 mid 的写法的话,注意要判断 \([l,r]\) 可能不在当前的区间的情况:
void update(int l,int r,int fa,int val){//l,r表示询问的区间
if(a[t[fa].r+1]<=l||a[t[fa].l]>=r)return;//剪枝
if(a[t[fa].l]>=l&&a[t[fa].r+1]<=r){
t[fa].cnt+=val;
pushup(fa);//小细节,直接pushup来更新长度当然你也可以直接把pushup给搬过来
return;
}
update(l,r,ls(fa),val);
update(l,r,rs(fa),val);
pushup(fa);//别忘了pushup啊qwq
return;
}
完整代码:
#include<bits/stdc++.h>
#define int long long//十年OI一场空,_______
#define ls(x) (x<<1)
#define rs(x) ((x<<1)|1)
using namespace std;
int a[200010],n,ans;//离散化数组
struct line{//线段
int l,r,h,w;//左长度,右长度和此时的高,以及他的权值
bool operator<(const line &a)const{
return h<a.h;//从低到高排序
}
}line[200010];//2n条线段
struct Node{//线段树节点
int l,r,sum,cnt;
//l和r表示t[i]维护a[l]到a[r+1]的区间
//sum表示目前这个区间包含的线段的长度
//cnt表示目前有多少个矩形完全包含这个线段
}t[8000010];//2n个点再加上四倍空间就是8倍空间
void pushup(int x){
if(t[x].cnt){//这个线段被覆盖过
t[x].sum=a[t[x].r+1]-a[t[x].l];//因为a[r+1]-a[l]的长度才是a[l]到a[r]的长度
}else{
t[x].sum=t[ls(x)].sum+t[rs(x)].sum;
}
return;
}
void build(int l,int r,int fa){//fa就是下标,个人习惯见谅
t[fa].r=r,t[fa].l=l,t[fa].sum=0,t[fa].cnt=0;
if(l==r){
return;
}
int mid=(l+r)>>1;
build(l,mid,ls(fa));
build(mid+1,r,rs(fa));
return;
}
void update(int l,int r,int fa,int val){//l,r表示询问的区间
if(a[t[fa].r+1]<=l||a[t[fa].l]>=r)return;//剪枝
if(a[t[fa].l]>=l&&a[t[fa].r+1]<=r){
t[fa].cnt+=val;
pushup(fa);//小细节,直接pushup来更新长度当然你也可以直接把pushup给搬过来
return;
}
update(l,r,ls(fa),val);//由于我们有剪枝,就不用判断了
update(l,r,rs(fa),val);
pushup(fa);//别忘了pushup啊qwq
return;
}
signed main(){
cin>>n;
for(int i=1;i<=n;i++){
int x,y,x2,y2;//定义y1过不了编译,我也不知道为什么
cin>>x>>y>>x2>>y2;
if(x>x2)swap(x,x2);
if(y>y2)swap(y,y2);//必须保证x<x2,y<y2
line[(i<<1)-1]={y,y2,x,1};//下边
line[i<<1]={y,y2,x2,-1};//上边
a[(i<<1)-1]=y,a[i<<1]=y2;
}
n<<=1;//线段数是矩形数的两倍
sort(line+1,line+n+1);
sort(a+1,a+n+1);
int cnt=unique(a+1,a+n+1)-a-1;
build(1,cnt-1,1);//注意cnt需要-1,因为cnt的点的数量
for(int i=1;i<n;i++){//最后一条边就不用更新了
update(line[i].l,line[i].r,1,line[i].w);//更新
ans+=t[1].sum*(line[i+1].h-line[i].h);//计算答案
}
cout<<ans<<endl;
return 0;
}//完结撒花!!!
3. 扫描线矩形周长并
有 \(n\) 个矩形,每个矩形的下表为 \(x_i\),\(y_i\),\(x2_i\),\(y2_i\),求这些矩形的周长并。
\(n\le10^4\),\(x_i,x2_i,y_i,y2_i\le 10^9\)。
同样,我们先给个例子:

回想一下我们用扫描先写矩形面积并的方法。
我们先考虑怎样维护线段树,我们现在已知要维护这些:
- 这个区间的 \(l,r\) 端点
- 这个区间是否被完全包含
- 这个区间被包含的长度
- 这个区间被完整覆盖的次数
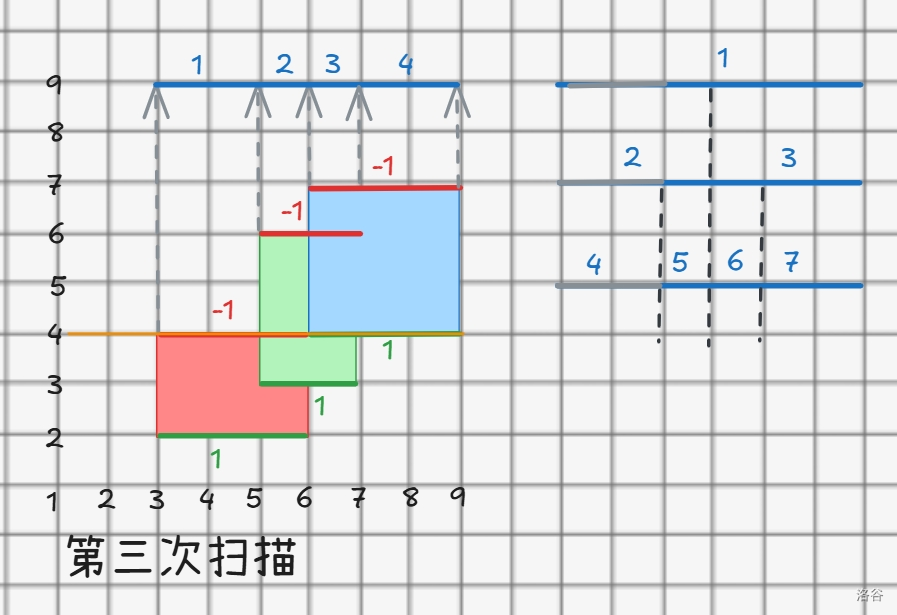
如果我们再考虑的细一点,不难发现:横边总长 \(= \sum |\) 上次扫描到的总长 \(-\) 这次扫描到的总长 \(|\),这个可以自己编个样例看看。
这些信息已经能够维护横边了,我们再考虑怎样维护竖边:我们能否维护这个区间的竖边边数呢?

答案是肯定的,并且不难发现,这个区间的竖边边数就等同于这个区间所包含的完整的线段数 \(\times 2\),比如说上图的第三次扫描,我们会发现它一共包含了 \(2\) 条横边,也就是第三次会扫描到 \(4\) 条竖边。
注意:相连的横边算作是一条横边,因为中间的竖边会被覆盖。
但是,如果单单是这样维护也有个问题,那就是如果两个子区间内包含的间连起来了(听不懂没关系,看图就行),这时答案不久错了?

很明显是错的,我们试着新维护两个值,表示这个区间的左、右端点是否被覆盖,这样就能判断左子区间的右端点,和右子区间的左端点,是否被覆盖就行了。
最后,对于每次扫描的结果,竖边数。\(\times\) 两条线的高度差距就是整个图形的竖边周长了。
当然,你也可以向横边一样对竖边重新扫描一次,不过那样码量更大。
剩下的步骤就和矩形面积并差不多了!
4. 扫描线矩形周长并代码
模板题:P1856
完整代码
#include<bits/stdc++.h>
#define int long long//_______,_______(100分)
#define ls(x) (x<<1)
#define rs(x) ((x<<1)|1)
using namespace std;
int a[200010],n;
struct line{
int l,r,h,w;
bool operator<(const line &a)const{
if(h==a.h)return w>a.w;//注意:加法优先
return h<a.h;
}
}line[200010];
struct Node{
int l,r,sum,cnt,cnt2;//cnt2就是这个区间被完整覆盖的次数
//[1,3][2,4]算一次[1,4],原因我在上文说过
bool fl,fr;//左右端点是否被覆盖
}t[800010];
void pushup(int x){
if(t[x].cnt){
t[x].sum=(a[t[x].r+1]-a[t[x].l]);
t[x].cnt2=1;
t[x].fl=t[x].fr=true;//因为被完全包含了,所以算被覆盖
}
else{
t[x].sum=t[ls(x)].sum+t[rs(x)].sum;
t[x].cnt2=t[ls(x)].cnt2+t[rs(x)].cnt2;//不必多说
t[x].fl=t[ls(x)].fl,t[x].fr=t[rs(x)].fr;//继承左右区间的覆盖情况
if(t[ls(x)].fr&&t[rs(x)].fl){//特殊情况,实际包含的区间需要-1
t[x].cnt2--;
}
}
return;
}
void build(int l,int r,int fa){//fa就是节点编号,个人习惯见谅x2
t[fa].l=l,t[fa].r=r,t[fa].sum=t[fa].cnt=t[fa].cnt2=0,t[fa].fl=t[fa].fr=false;
if(l>=r)return;
int mid=(l+r)>>1;
build(l,mid,ls(fa));
build(mid+1,r,rs(fa));
return;
}
void update(int l,int r,int fa,int k){
if(a[t[fa].r+1]<=l||a[t[fa].l]>=r){//剪枝,剪掉不在区间内的情况
return;
}
if(a[t[fa].l]>=l&&a[t[fa].r+1]<=r){
t[fa].cnt+=k;
pushup(fa);//这里直接写pushup方便很多
return;
}
update(l,r,ls(fa),k);
update(l,r,rs(fa),k);
//注意:如果你不用剪枝写法,需要判断[l,r]是否再区间内,不然就死循环了
pushup(fa);
return;
}
signed main(){
int n,ans=0,last=0;
cin>>n;
for(int i=1;i<=n;i++){
int x,y,x2,y2;
cin>>x>>y>>x2>>y2;
if(x>x2)swap(x,x2);
if(y>y2)swap(y,y2);
line[(i<<1)-1]={y,y2,x,1};
line[i<<1]={y,y2,x2,-1};
a[(i<<1)-1]=y,a[i<<1]=y2;
}
n<<=1;
sort(a+1,a+n+1);
sort(line+1,line+n+1);
int cnt=unique(a+1,a+n+1)-a-1;
build(1,cnt-1,1);
for(int i=1;i<n;i++){
update(line[i].l,line[i].r,1,line[i].w);
ans+=abs(t[1].sum-last)+(t[1].cnt2<<1)*(line[i+1].h-line[i].h);
last=t[1].sum;
}
ans+=line[n].r-line[n].l;//记得加上最后一条边
cout<<ans<<endl;
return 0;
}//完结撒花!
5. 闲话
蒟蒻不才,膜拜大佬,如果有任何错字等问题,请在评论区提醒我。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号