L5 Convex Optimization & Gradient-based Optimization Algorithm

Convex Optimization & Gradient-based Optimization Algorithm

凸优化

考虑优化问题：

\[\min_{\theta \in \mathbb{R}^d} \mathcal{L}(\theta) \]

• 如果 \(\mathcal{L}(\theta)\) 是一个凸函数，则该优化问题称为凸优化。
• 否则，称为非凸优化。

定义：凸函数

一个函数 \(\mathcal{L}: \mathbb{R}^d \rightarrow \mathbb{R}\) 是凸的，如果对于所有 \(\theta, w \in \mathbb{R}^d\) 和任何 \(\alpha \in [0, 1]\)，

\[\mathcal{L}(\alpha\theta + (1-\alpha)w) \leq \alpha\mathcal{L}(\theta) + (1-\alpha)\mathcal{L}(w) \]

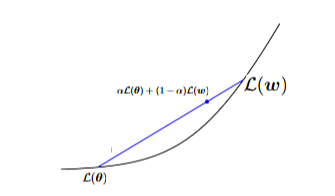
该图像展示了一个图形，说明了凸函数的定义。图形显示了一个表示函数 \(\mathcal{L}\) 的曲线，以及连接曲线上两个点的线段。线段位于曲线之上或与曲线重合，直观地表示了定义中的不等式。

• 几何直觉： 均匀向上的曲率。
• 简单例子： \(\mathcal{L}(\theta) = \theta\)，\(\mathcal{L}(\theta) = \theta^2\)，\(\mathcal{L}(|\theta|)\)，\(\mathcal{L}(|\theta|)^2\)。

一阶凸性特征

假设 \(\mathcal{L} : \mathbb{R}^d \to \mathbb{R}\) 是可微的。\(\mathcal{L}\) 是凸的当且仅当对于所有 \(\theta, w \in \mathbb{R}^d\)，

\[L(w) \ge L(\theta) + \nabla L(\theta)^T (w - \theta) \]

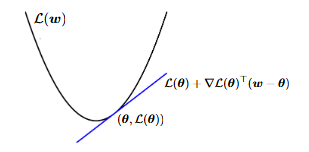
图像显示了一个凸函数 \(L(w)\) 及其在点 \((\theta, L(\theta))\) 的切线。切线由方程 \(L(\theta) + \nabla L(\theta)^T (w - \theta)\) 表示。

• 该定理常用于分析。

• 含义：\(\nabla L(\theta^*) = 0\) 当且仅当 \(\theta^*\) 是全局最小值。

• 这就是我们如何找到最小二乘法（线性回归）的最优参数。

二阶凸性特征

定理：通过海森矩阵判断凸性

设 \(\mathcal{L} : \mathbb{R}^d \to \mathbb{R}\) 是二次连续可微的。当且仅当其海森矩阵是半正定的（PSD），即：

\[\mathbf{d}^{\top} \nabla^2 \mathcal{L}(\boldsymbol{\theta}) \mathbf{d} \geq 0 \quad \forall \mathbf{d} \in \mathbb{R}^d, \quad \forall \boldsymbol{\theta} \in \mathbb{R}^d. \]

• 如果目标函数是二次连续可微的，可以通过这种方式测试凸性。

示例：机器学习中的凸实例

我们有以下函数是凸的：

• 最小二乘法：

  \[L(\theta) = ||X\theta - y||_2^2 \]
  \[L(\theta) = (X\theta - y)^T (X\theta - y) = \theta^T X^T X \theta - 2y^T X \theta + y^T y \]
  \[ \frac{\partial}{\partial \theta} \left( \theta^T X^T X \theta \right) = 2X^T X \theta \]
  \[\nabla L(\theta) = 2X^T X \theta - 2X^T y \]

  凸性因为海森矩阵 \(\nabla^2 L(\theta) = 2X^T X\) 是正半定的。

• 逻辑回归：

  \[L(\theta) = \frac{1}{n} \sum_{i=1}^n \log(1 + \exp(-y_i \cdot \theta^T x_i)). \]

• 多类逻辑回归：

  \[L(\theta) = -\frac{1}{n} \sum_{i=1}^n \sum_{k=1}^K 1_{\{y_i=k\}} \log \left( \frac{\exp(\theta_k^T x_i)}{\sum_{j=1}^K \exp(\theta_j^T x_i)} \right). \]

• 支持向量机学习问题（稍后）。

凸优化的优势

• 没有局部最小值。零梯度意味着全局最优解，对应于 \(\hat{\theta}\)。
• 尽管我们通常没有闭式解，但我们有可靠且高效的算法来找到全局最小值，即提供零梯度的点。
• 有一套完善的凸优化算法工具。

算法：

• 基于梯度的方法。
• 次梯度方法。
• ...

基于梯度的优化算法

迭代算法

从初始点 \(\theta_0\) 开始，迭代算法 \(A\) 将生成一系列迭代

\[\theta_{k+1} = A(\theta_k) \]

对于 \(k = 0, 1, 2, \dots\)，

• \(k\) 代表迭代，是一个索引数字。
• \(\theta_k\) 代表第 \(k\) 次迭代的结果。

在实践中，\(A\) 通常具有什么形式？

\[\theta_{k+1} = \theta_k + \mu_k d_k \]

• \(\Re \ni \mu_k > 0\) 是步长 / 学习率。
• \(d_k \in \mathbb{R}^d\) 是搜索方向，通常依赖于 \(\theta_k\)。
• 关键是在每次迭代中选择一个合适的方向 \(d_k\)。

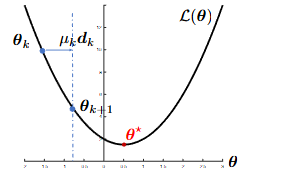
需要确定的事项：

• 初始点\(\theta_0\)（适用于凸优化）。
• 搜索方向\(d_k\)。
• 学习率\(\mu_k\)。
• 停止标准。

搜索方向 \(d_k\)

目标：

\[\min_{\theta \in \mathbb{R}^d} \mathcal{L}(\theta) \]

要求：
\(d_k\) 应该指向一个能够降低函数值的方向。

命题：下降方向
假设 \(\mathcal{L}\) 是连续可微的，如果存在一个 \(d\) 使得

\[\nabla \mathcal{L}(\theta)^T d < 0 \]

那么，存在一个 \(\tilde{\mu} > 0\) 使得

\[ \mathcal{L}(\theta + \mu d) < \mathcal{L}(\theta) \]

对于所有 \(\mu \in (0, \tilde{\mu})\)。因此，\(d\) 是在 \(\theta\) 处的下降方向。（该命题可以通过泰勒定理证明。）

梯度下降

• 这个命题告诉我们：在第 \(k\) 次迭代中，找到一个 \(d_k\) 使得

  \[\nabla \mathcal{L}(\theta_k)^T d_k < 0 \]

  那么，\(d_k\) 必须是当前迭代点 \(\theta_k\) 的下降方向。

因此，一个可能的选择是

\[d_k = -\nabla \mathcal{L}(\theta_k) \]

结果算法

梯度下降 (GD)

\[ \theta_{k+1} = \theta_k - \mu_k \nabla \mathcal{L}(\theta_k) \]

可以等价地写为

\[\theta_{k+1} = \underset{\theta \in \mathbb{R}^d}{\operatorname{argmin}} \mathcal{L}(\theta_k) + \nabla \mathcal{L}(\theta_k)^\top (\theta - \theta_k) + \frac{1}{2\mu_k} \|\theta - \theta_k\|_2^2 \]

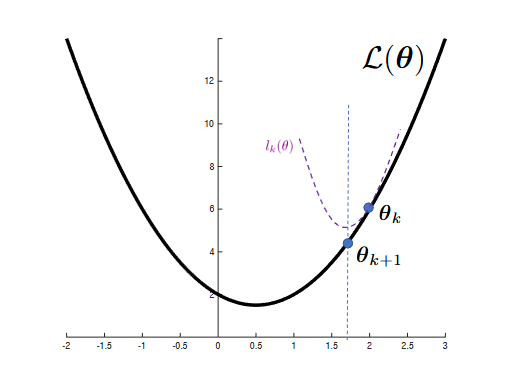
• \(\mathcal{L}(\theta_k) + \nabla \mathcal{L}(\theta_k)^\top (\theta - \theta_k)\) 是在 \(\theta_k\) 处对 \(\mathcal{L}\) 的线性近似。
• \(\frac{1}{2\mu_k} \|\theta - \theta_k\|_2^2\) 是与学习率 \(\mu_k\) 相关的近端项。

梯度下降：解释

\[\theta_{k+1} = \underset{\theta \in \mathbb{R}^d}{\operatorname{argmin}} \left\{ l_k(\theta) := \mathcal{L}(\theta_k) + \nabla \mathcal{L}(\theta_k)^T (\theta - \theta_k) + \frac{1}{2\mu_k} \|\theta - \theta_k\|_2^2 \right\} \]

• \(l_k(\theta)\) 是 \(\theta\) 的二次函数，即二次近似
• 在每次迭代中，我们有封闭形式的更新，即梯度下降算法

\[\theta_{k+1} = \theta_k - \mu_k \nabla \mathcal{L}(\theta_k) \]

几乎通用的算法设计策略
通过解决一系列更简单的子问题来解决原始问题。

更简单的子问题可以从两个方面进行解释：

1. \(\mathcal{L}(\theta)\) 的线性近似 + 一个近端项
2. \(\mathcal{L}(\theta)\) 的二次近似 \(l_k(\theta)\)

一个有用的算法设计框架

假设任务是 \(\min_{\theta \in \mathbb{R}^d} \mathcal{L}(\theta)\)，我们可以设计一个算法如下：

\[\theta_{k+1} = \underset{\theta \in \mathbb{R}^d}{\operatorname{argmin}} \left\{ q_k(\theta) + \frac{1}{2\mu_k} \|\theta - \theta_k\|^2_2 \right\} \]

\(\mu_k\) 是类似学习率的量。

• 当 \(q_k(\theta)\) 是 \(\mathcal{L}\) 的线性近似时 \(\implies\) 梯度下降 gradient descent
• 当 \(q_k(\theta)\) 是 \(\mathcal{L}\) 的二阶近似时 \(\implies\)​ 牛顿法 Newton’s method
• 当 \(q_k(\theta)\) 是 \(\mathcal{L}\) 本身时 \(\implies\) 近端点法 proximal point method
• 当 \(q_k(\theta)\) 是 \(\mathcal{L}\) 的单分量线性近似时 \(\implies\) 随机梯度下降 (SGD) stochastic gradient descent (SGD)
  ...

许多优化算法遵循这个设计框架。

收敛问题

• 为了解决 \(\min_{\theta \in \mathbb{R}^d} \mathcal{L}(\theta)\)，我们无法解析地获得解 \(\hat{\theta}\)。
• 设计一个迭代算法，从 \(\theta_0\) 开始，它将生成 \(\{\theta_0, \theta_1, \theta_2, \dots, \theta_k, \dots\}\)。

算法的收敛性分析关注：

• \(\theta_k\) 是否会收敛到解 \(\hat{\theta}\)？即
  \[\lim_{k \to \infty} \theta_k \stackrel{?}{=} \hat{\theta} \]

• 如果是，这种收敛的速度是多少？

GD的收敛性

• 假设\(L\)是凸的且可微的，并且具有Lipschitz连续梯度，参数为\(L\)，
  \[\|\nabla L(w) - \nabla L(u)\|_2 \le L\|w - u\|_2, \quad \forall w, u ~~ 在LR中满足凸性和Lipschitz梯度。 \]

Lipschitz 连续梯度（Lipschitz Continuous Gradient）：这表示梯度变化不会太快，函数的曲线是“平滑”的

定理：GD的收敛性及收敛速率
具有恒定学习率\(\mu_k = \mu = 1/L\)的梯度下降满足

\[L(\theta_k) - L(\hat{\theta}) \le \frac{\|\theta_0 - \hat{\theta}\|_2^2}{2k} \]

• \(L(\theta_k)\)以\(O(1/k)\)的速率收敛到\(L(\hat{\theta})\)。

• 这并不意味着\(\{\theta_k\}\)以某种速率收敛到\(\hat{\theta}\)。
• \(L(\theta_k) - L(\hat{\theta})\)称为次优性间隙。

学习率

学习率的选择

梯度下降：

\[\theta_{k+1} = \theta_k - \mu_k \nabla \mathcal{L}(\theta_k) \]

• 在实践中，学习率最简单的选择是使用恒定学习率，即对于某个相对较小的 \(\mu\)，有 \(\mu_k = \mu\)，其中 \(k = 0, 1, \dots\)。一些典型的猜测值：\(0.05, 0.01, 0.005, \dots\)
  • 在机器学习中，较大的模型通常需要较小的恒定学习率。
• 在优化中，也可以使用某种线搜索方法以自适应的方式选择 \(\mu_k\)。
  • 然而，在机器学习中，线搜索并不被使用，因为它浪费了太多的计算。
• 当我们研究随机梯度下降时，将介绍衰减学习率的调度。

梯度下降的停止标准

典型的停止标准：

• 固定总迭代次数为 \(K\)。
• 当 \(\| \nabla \mathcal{L}(\theta_k) \|_2\) 很小时停止，比如 \(\| \nabla \mathcal{L}(\theta_k) \|_2 \leq \epsilon\)。
  • 因为在最小值 \(\hat{\theta}\) 处，\(\| \nabla \mathcal{L}(\hat{\theta}) \|_2 = 0\)。
• 当 \(\| \theta_{k+1} - \theta_k \|_2\) 很小时时停止，比如 \(\| \theta_{k+1} - \theta_k \|_2 \leq \epsilon\)。
• 在机器学习中，当验证误差开始增加时停止。

将GD应用于LR

给定一组训练数据点：\(\{(x_1, y_1), \dots, (x_n, y_n)\}\)，二元逻辑回归的学习问题为：

\[\hat{\theta} = \underset{\theta \in \mathbb{R}^d}{\operatorname{argmin}} \mathcal{L}(\theta) := \frac{1}{n} \sum_{i=1}^n \log(1 + \exp(-y_i \cdot \theta^\top x_i)) \]

• \(\mathcal{L}\) 是凸的，并且具有Lipschitz梯度。
• 我们可以应用梯度下降法（GD）：

\[\theta_{k+1} = \theta_k - \mu_k \nabla \mathcal{L}(\theta_k) \]

如果学习率选择得当，它具有收敛保证：\(\mathcal{L}(\theta_k) - \mathcal{L}(\hat{\theta}) \leq \mathcal{O}(1/k)\)。

• 主要元素包括：1. 计算梯度并形成搜索方向。2. 确定学习率（通常是一个小常数）。3. 当满足停止标准时停止。
• 需要知道如何通过链式法则计算梯度。

一些GD的优缺点

优点：

• GD实现简单。
• 对几乎所有可微凸问题效果良好。

缺点：

• GD的收敛速度相对较慢。

加速梯度下降

带动量的梯度下降(Gradient Descent with Momentum)

GD:

\[\theta_{k+1} = \theta_k - \mu_k \nabla \mathcal{L}(\theta_k) \]

• GD在每次迭代中强制实现充分下降，留下探索更有效搜索方向的可能性。
• 加速梯度下降方法的一个相当流行的技术是动量技术：

\[\theta_{k+1} = \theta_k - \mu_k \nabla \mathcal{L}(\theta_k) + \beta_k (\theta_k - \theta_{k-1}) \]

（动量）

等效形式：

\[\theta_{k+1} = \theta_k - m_k \]

\[m_k = \mu_k \nabla \mathcal{L}(\theta_k) + \beta_k m_{k-1} \]

• 由于Boris T. Polyak提出。
• 每次迭代的时间成本几乎与GD相同。
• 在实践中广泛使用，特别是在Adam算法中。

动量加速：几何解释

梯度下降（GD）： \(\theta_{k+1} = \theta_k - \mu_k \nabla \mathcal{L}(\theta_k)\)

带动量的梯度下降：\(\theta_{k+1} = \theta_k - \alpha_k \nabla \mathcal{L}(\theta_k) + \beta_k (\theta_k - \theta_{k-1})\)

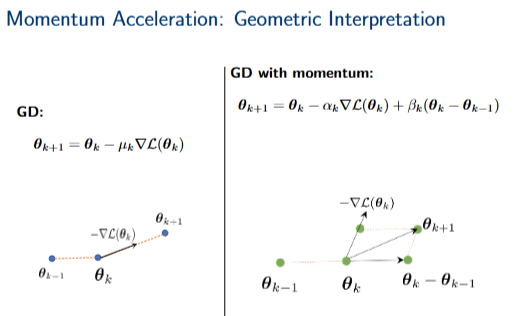
左侧图示了梯度下降（GD）的几何解释，其中一个点表示当前参数 \(\theta_k\)，另一个点表示下一个参数 \(\theta_{k+1}\)。从 \(\theta_k\) 指向 \(\theta_{k+1}\) 的向量代表了更新步长，其方向与负梯度 \(-\nabla \mathcal{L}(\theta_k)\) 相同。

右侧图示了带动量的梯度下降（GD with momentum）的几何解释。除了当前参数 \(\theta_k\) 和下一个参数 \(\theta_{k+1}\)，还引入了前一个参数 \(\theta_{k-1}\)。更新步长由两部分组成：一部分是与负梯度 \(-\nabla \mathcal{L}(\theta_k)\) 成比例的向量，另一部分是与前一步的更新向量 \((\theta_k - \theta_{k-1})\) 成比例的向量。这两个向量的叠加决定了最终的更新方向和大小。

涅斯特罗夫加速梯度下降法Nesterov’s Accelerated Gradient Descent

Nesterov加速

梯度下降（GD）：

\[\theta_{k+1} = \theta_k - \mu_k \nabla \mathcal{L}(\theta_k) \]

另一种非常有用的加速GD的技术是Nesterov加速梯度下降（AGD）：

\[\begin{aligned} \theta_{k+1} &= w_k - \mu_k \nabla \mathcal{L}(w_k) \\ w_k &= \theta_k + \frac{k-1}{k+2}(\theta_k - \theta_{k-1}) \end{aligned} \]

• Nesterov加速的动机来自动量，但在外推点上评估梯度，并且对\(\beta_k\)有特定选择。
• 每次迭代的时间成本几乎与GD相同。
• 在实践中广泛使用。

Nesterov加速：几何解释

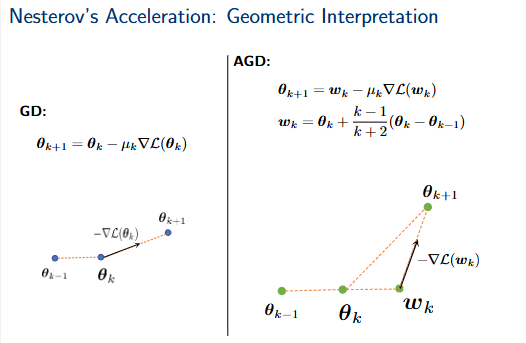
梯度下降（GD）：\(\theta_{k+1} = \theta_k - \mu_k \nabla \mathcal{L}(\theta_k)\)

加速梯度下降（AGD）：\(\theta_{k+1} = w_k - \mu_k \nabla \mathcal{L}(w_k)\) \(w_k = \theta_k + \frac{k-1}{k+2}(\theta_k - \theta_{k-1})\)

左侧图展示了梯度下降（GD）的几何解释，其中一个点 \(\theta_{k-1}\) 移动到 \(\theta_k\)，然后根据负梯度 \(-\nabla \mathcal{L}(\theta_k)\) 移动到 \(\theta_{k+1}\)。

右侧图展示了加速梯度下降（AGD）的几何解释。从 \(\theta_{k-1}\) 到 \(\theta_k\) 的移动，然后计算一个动量项 \(\frac{k-1}{k+2}(\theta_k - \theta_{k-1})\)，将 \(\theta_k\) 移动到 \(w_k\)。最后，根据负梯度 \(-\nabla \mathcal{L}(w_k)\) 从 \(w_k\) 移动到 \(\theta_{k+1}\)。

AGD的收敛性

► 假设 \(L\) 是凸的且可微的，并且具有Lipschitz连续梯度，参数为\(L\)（例如，线性回归问题）。

定理：AGD的收敛性
具有恒定学习率 \(\mu_k = \mu = 1/L\) 的加速梯度下降满足

\[\mathcal{L}(\theta_k) - \mathcal{L}(\hat{\theta}) \le \frac{2L ||\theta_0 - \hat{\theta}||^2}{(k+1)^2} \]

► \(\mathcal{L}(\theta_k)\)以 \(O(1/k^2)\) 的速度收敛到 \(\mathcal{L}(\hat{\theta})\)。
► 这个速度比GD快得多，后者仅具有 \(O(1/k)\) 的收敛速度。 AGD 收敛速度更快